Exercise 2.2Z: Distortion Power again

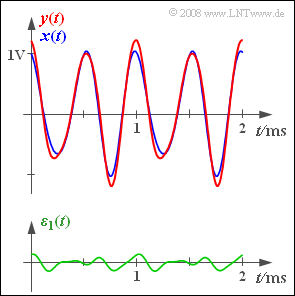
Am Eingang der betrachteten Funktionseinheit, die nicht näher spezifiziert wird, liegt das in der Grafik blau dargestellte periodische Signal x(t) an. Dieses ist durch das Spektrum des dazugehörigen analytischen Signals gegeben:

$$X_+(f) = {1 \,\rm V} \cdot {\rm \delta}(f- {2 \,\rm kHz}) \\ + {0.2 \,\rm V} \cdot {\rm e}^{\rm j \cdot 90^{\circ} } \cdot \delta(f- {3 \,\rm kHz}).$$

Diese Spektralfunktion ergibt sich aus dem üblichen Spektrum X(f), in dem alle Anteile bei negativen Frequenzen abgeschnitten und die bei den positiven Frequenzen verdoppelt werden. Weitere Angaben zum analytischen Signal und dessen Spektrum finden Sie im Kapitel 4.2 des Buches „Signaldarstellung”.

Das Spektrum des analytischen Signals am Ausgang der Funktionseinheit lautet:

$$Y_+(f) = {1.1 \,\rm V} \cdot {\rm \delta}(f- {2 \,\rm kHz}) \\ + {0.25 \,\rm V} \cdot {\rm e}^{\rm j \cdot 60^{\circ} } \cdot \delta(f- {3 \,\rm kHz})+ {0.05 \,\rm V} \cdot {\rm e}^{-\rm j \cdot 90^{\circ} } \cdot \delta(f- {5 \,\rm kHz}).$$

Die untere Skizze zeigt das Differenzsignal ε(t) = y(t) – x(t). Ein Maß für die im System entstandenen Verzerrungen ist die auf den Widerstand R = 1 Ω bezogene „Verzerrungsleistung”.

$$P_{\rm V} = \overline{\varepsilon^2(t)} = \frac{1}{T_{\rm 0}} \cdot \int\limits_{0}^{ T_{\rm 0}} {\varepsilon^2(t) }\hspace{0.1cm}{\rm d}t.$$

Anzumerken ist, dass diese auch im Spektralbereich – und zudem einfacher – berechnet werden kann.

In analoger Weise ist die Leistung P_x des Eingangssignals x(t) definiert. Als quantitatives Maß für die Stärke der Verzerrungen wird das Signal–zu–Verzerrungs–Leistungsverhältnis angegeben, das meistens logarithmisch in dB dargestellt wird:

$$10 \cdot {\rm lg} \hspace{0.1cm}\rho_{\rm V} = 10 \cdot {\rm lg} \hspace{0.1cm} \frac{ P_{x}}{P_{\rm V}} \hspace{0.05cm}.$$

Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 2.1.

Die Leistung eines Signals x(t) kann auch aus der Spektralfunktion X(f) berechnet werden:

$$P_{x} =\frac{1}{T_{\rm 0}} \cdot\int\limits_{-\infty}^{ \infty} x^2(t)\hspace{0.1cm}{\rm d}t = \frac{1}{T_{\rm 0}} \cdot \int\limits_{-\infty}^{ \infty} |X(f)|^2\hspace{0.1cm}{\rm d}f.$$

Fragebogen

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.

	Es ist x(t) = 1V · cos(2π · 2kHz · t) + 0.2V · cos(2π · 3kHz · t).
	Die Periodendauer ist T₀ = 1 ms.
	Die Periodendauer ist T₀ = 2 ms.