Properties of Nyquist Systems

Erstes Nyquistkriterium im Zeitbereich

Für dieses Kapitel wurde vorausgesetzt, dass die Detektion eines Symbols nicht durch Nachbarimpulse beeinträchtigt werden soll. Dies erreicht man durch die Detektion des Signals

\(d(t) = \sum \limits_{\it (\nu)} a_\nu \cdot g_d ( t - \nu T)\)

zu den Zeitpunkten νT immer dann, wenn der Detektionsgrundimpuls g_d(t)

auf den Bereich | t | < T beschränkt ist, was für das Kapitel 1.2 vorausgesetzt wurde, oder
äquidistante Nulldurchgänge zu den Zeitpunkten νT aufweist.

Aus Gründen einer möglichst einfachen Darstellung wird im Kapitel 1.3 das Detektionsstörsignal d_N(t) als vernachlässigbar klein angenommen.

: Man bezeichnet einen Detektionsgrundimpuls mit den Eigenschaften

\[g_d ( t = \nu T)= 0 \hspace{0.3cm}{\rm{f\ddot{u}r}}\hspace{0.3cm} \nu = \pm 1, \pm 2,\pm 3,\hspace{0.05cm}...\]

als Nyquistimpuls g_Nyq(t), benannt nach dem Physiker Harry Nyquist.

: Die Grafik zeigt das Detektionssignal d(t) eines solchen Nyquistsystems. Rot gepunktet sind die (gewichteten und verschobenen) Nyquistimpulse a_ν · g_Nyq(t – νT) eingezeichnet.

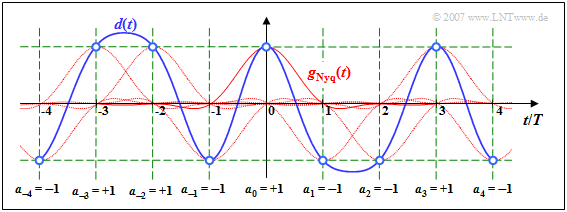
Zu den Detektionszeitpunkten gilt d(νT) = a_ν · g_Nyq(0), wie aus den blauen Kreisen und dem grünen Raster hervorgeht. Die Nachläufer der vorangegangenen Impulse (ν < 0) sowie die Vorläufer der nachfolgenden Impulse (ν > 0) beeinflussen beim Nyquistsystem die Detektion des Symbols a₀ nicht.

Der Vollständigkeit halber sei erwähnt, dass für diese Grafik der Detektionsgrundimpuls

\(g_{\rm Nyq} ( t )= g_0 \cdot {\rm si} \left ( \frac{\pi \cdot t}{T}\right)\cdot {\rm si} \left ( \frac{\pi \cdot t}{2 \cdot T}\right)\)

mit trapezförmigem Spektrum und dem Rolloff–Faktor r = 0.5 zugrunde liegt. Dieser wurde bereits im Kapitel 3 des Buches „Signaldarstellung” behandelt.

Erstes Nyquistkriterium im Frequenzbereich

Harry Nyquist hat die Bedingung für eine impulsinterferenzfreie Detektion nicht nur für den Zeitbereich formuliert, sondern 1928 auch das entsprechende Kriterium im Frequenzbereich angegeben.
Erstes Nyquistkriterium: Erfüllt das Spektrum G_d(f) des Detektionsgrundimpulses die Bedingung

\(\sum \limits_{\it k = -\infty}^{+\infty} G_d \left ( f - \frac{k}{T} \right)= g_0 \cdot T = {\rm const.} \hspace{0.05cm}, \)

so ist g_d(t) ein Nyquistimpuls mit äquidistanten Nulldurchgängen zu den Zeitpunkten νT (ν ≠ 0) und der Amplitude g_d(t = 0) = g₀. Hinweis: Sie finden den Beweis auf Beweis des ersten Nyquistkriteriums.
Die nachfolgende Grafik zeigt zwei Nyquistspektren. Das Spektrum

\(G_1(f) = \left\{ \begin{array}{c} g_0 \cdot T \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} |f| < {1}/({2T})\hspace{0.05cm}, \\ |f| > {1}/({2T}) \hspace{0.1cm} \\ \end{array}\)

erfüllt offensichtlich die oben formulierte Bedingung und zwar mit der kleinstmöglichen Bandbreite. Der dazugehörige Nyquistimpuls g₁(t) = g₀ · si(πt/T) klingt sehr langsam ab, nämlich asymptotisch mit 1/t.

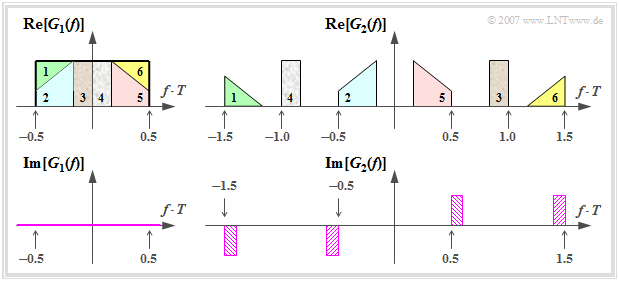
Der rechts oben dargestellte Realteil des Spektrums G₂(f) wurde aus dem Rechteckspektrum G₁(f) durch Verschiebung von Teilstücken um 1/T nach rechts oder links konstruiert. Wegen

\(\sum \limits_{\it k = -\infty}^{+\infty} {\rm Re}\left[G_2 \left ( f - \frac{k}{T} \right)\right]= g_0 \cdot T \hspace{0.05cm}, \hspace{1cm}\sum \limits_{\it k = -\infty}^{+\infty} {\rm Im}\left[G_2 \left ( f - \frac{k}{T} \right)\right]= 0\)

handelt es sich bei G₂(f) ebenfalls um ein Nyquistspektrum. Beim Imaginärteil heben sich die jeweils gleich schraffierten Anteile, die jeweils um 2/T auseinander liegen, auf. Die Angabe des dazugehörigen Nyquistimpulses g₂(t) ist allerdings sehr kompliziert.

Beweis des ersten Nyquistkriteriums

Wir gehen von der ersten Nyquistbedingung im Zeitbereich aus:\[g_{\rm Nyq}(\nu T) = \left\{ \begin{array}{c} g_0 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} \nu = 0 \hspace{0.05cm}, \\ \nu \ne 0 \hspace{0.1cm}. \\ \end{array}\]
Aus dem zweiten Fourierintegral erhält man somit für ν ≠ 0:\[g_{\rm Nyq}(\nu T) = \int_{-\infty}^{+\infty}G_{\rm Nyq}(f) \cdot {\rm e}^{ \hspace{0.05cm}{\rm j} \hspace{0.05cm}2 \pi f \hspace{0.05cm}\nu \hspace{0.05cm}T}\,{\rm d} f = 0 \hspace{0.05cm}.\]
Zerlegt man das Fourierintegral in Teilintegrale der Breite 1/T, so lauten die Bedingungsgleichungen:\[\sum_{k = -\infty}^{+\infty} \hspace{0.2cm} \int_{(k-1/2)/T}^{(k+1/2)/T}G_{\rm Nyq}(f) \cdot {\rm e}^{ \hspace{0.05cm}{\rm j} \hspace{0.05cm}2 \pi f \hspace{0.05cm}\nu \hspace{0.05cm}T}\,{\rm d} f = 0 \hspace{0.05cm}.\]
Mit der Substitution f ' = f + k/T folgt daraus:\[\sum_{k = -\infty}^{+\infty} \hspace{0.2cm} \int_{-1/(2T)}^{1/(2T)}G_{\rm Nyq}(f' - \frac{k}{T} ) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}2 \pi \hspace{0.05cm} \cdot \hspace{0.05cm} (f'- k/T) \hspace{0.05cm} \cdot \hspace{0.05cm}\nu \hspace{0.05cm}T}\,{\rm d} f ' = 0 \hspace{0.05cm}.\]
Für alle ganzzahligen Werte von k und ν gilt:\[{\rm e}^{-{\rm j} \hspace{0.05cm}2 \pi \hspace{0.05cm} k \hspace{0.05cm} \nu } = 1 \hspace{0.4cm} \Rightarrow \hspace{0.4cm}\sum_{k = -\infty}^{+\infty} \hspace{0.2cm} \int_{-1/(2T)}^{1/(2T)}G_{\rm Nyq}(f' - \frac{k}{T} ) \cdot {\rm e}^{{\rm j} \hspace{0.05cm}2 \pi \hspace{0.02cm}f' \hspace{0.02cm} \nu \hspace{0.05cm}T}\,{\rm d} f ' = 0 \hspace{0.05cm}.\]
Durch Vertauschen von Summation und Integration sowie Umbenennen von f ' in f folgt weiter:\[\int_{-1/(2T)}^{1/(2T)}\hspace{0.2cm} \sum_{k = -\infty}^{+\infty} G_{\rm Nyq}(f - \frac{k}{T} ) \cdot {\rm e}^{{\rm j} \hspace{0.05cm}2 \pi \hspace{0.02cm}f \hspace{0.02cm} \nu \hspace{0.05cm}T}\,{\rm d} f = 0 \hspace{0.05cm}.\]
Diese Forderung ist für alle ν ≠ 0 nur dann zu erfüllen, wenn die unendliche Summe unabhängig von f ist, also einen konstanten Wert besitzt:\[\sum_{k = -\infty}^{+\infty} G_{\rm Nyq}(f - \frac{k}{T} ) = K_{\rm Nyq} \hspace{0.05cm}.\]
Aus der vorletzten Gleichung erhält man gleichzeitig für ν = 0:\[\int_{-1/(2T)}^{1/(2T)}\hspace{0.2cm} \sum_{k = -\infty}^{+\infty} G_{\rm Nyq}(f - \frac{k}{T} ) \,{\rm d} f = K_{\rm Nyq} \cdot \frac{1}{T} = g_0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}K_{\rm Nyq} = g_0 \cdot T \hspace{0.05cm}.\]

1/T–Nyquistspektren (1)

Eine besondere Bedeutung für die Digitalsignalübertragung besitzen solche Nyquistspektren, die auf den Frequenzbereich –1/T ≤ f ≤ +1/T beschränkt und zusammenhängend sind. Die Grafik zeigt mit der Trapez–Charakteristik und der Cosinus–Rolloff–Charakteristik zwei diesbezügliche Varianten.

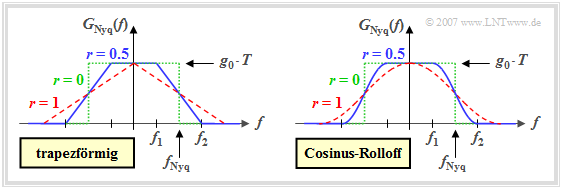
Für beide Nyquistspektren gilt in gleicher Weise:

Der Flankenabfall erfolgt zwischen den zwei Eckfrequenzen f₁ und f₂ punktsymmetrisch um die Nyquistfrequenz f_Nyq = 1/(2T) = (f₁ + f₂)/2. Das heißt, dass für 0 ≤ f ≤ f_Nyq gilt:\[G_{\rm Nyq}(f_{\rm Nyq}+f) + G_{\rm Nyq}(f_{\rm Nyq}-f) = g_0 \cdot T \hspace{0.05cm}.\]
G_Nyq(f) ist für alle Frequenzen | f | ≤ f₁ konstant gleich g₀ · T und für | f | ≥ f₂ identisch 0. Im Bereich zwischen f₁ und f₂ gilt:\[\frac{G_{\rm Nyq}(f)}{g_0 \cdot T } = \left\{ \begin{array}{c} \frac{f_2 - |f|}{f_2 -f_1 } \\ \\ \cos^2( \frac{\pi}{2}\cdot \frac{f_2 - |f|}{f_2 -f_1 }) \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{beim \hspace{0.15cm}Trapez}\hspace{0.05cm},} \\ \\ {\rm{\rm{beim \hspace{0.15cm}Cosinus-Rolloff}}\hspace{0.05cm}.} \\ \end{array}\]
Zur Parametrisierung der Flankensteilheit verwenden wir in beiden Fällen den Rolloff–Faktor, der Werte zwischen 0 und 1 (einschließlich dieser Grenzen) annehmen kann:\[r = \frac{f_2 -f_1 } {f_2 +f_1 } \hspace{0.05cm}.\]
Für r = 0 (f₁ = f₂ = f_Nyq) ergibt sich das Rechteck-Nyquistspektrum, während der Rolloff-Faktor r = 1 (f₁ = 0, f₂ = 2f_Nyq) ein dreieckförmiges bzw. cos²–Spektrum angibt – je nachdem, von welcher der beiden oben abgebildeten Grundstrukturen man ausgeht.

Hinweis: In der Literatur wird der Rolloff–Faktor auch oft mit α („alpha”) bezeichnet.

1/T–Nyquistspektren (2)

Betrachten wir nun die Nyquistimpulse. Beim trapezförmigem Spektrum mit Rolloff–Faktor r erhält man:\[g_{_{\rm Trapez}} ( t )= g_0 \cdot {\rm si} \left ( \frac{\pi \cdot t}{T}\right)\cdot {\rm si} \left ( \frac{\pi \cdot r \cdot t}{T}\right) \hspace{0.5cm}{\rm mit }\hspace{0.5cm}{\rm si}(x) = {\rm sin}(x)/x .\] Dagegen liefert die Fourierrücktransformation des Cosinus–Rolloff–Spektrums:\[g_{_{\rm CRO}} ( t )= g_0 \cdot {\rm si} \left ( \frac{\pi \cdot t}{T}\right)\cdot \frac{\cos(\pi \cdot r \cdot t/T)}{1 - (2 \cdot r \cdot t/T)^2 } \hspace{0.3cm}{\rm mit }\hspace{0.3cm}{\rm si}(x) = {\rm sin}(x)/x.\] Diese beiden Nyquistimpulse kann man im nachfolgend genannten Interaktionsmodul mit der Einstellung Δf · T = 1 betrachten und sich dabei den Einfluss des Rolloff–Faktors verdeutlichen:

Tiefpässe im Frequenz– und Zeitbereich Please add link

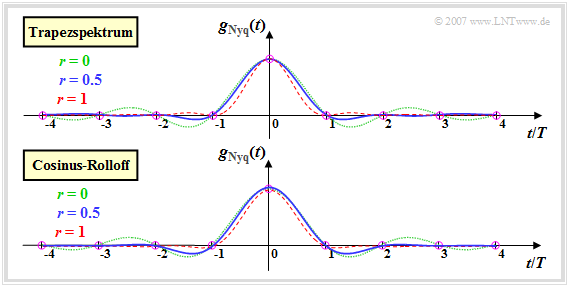
Die obere Grafik zeigt den Nyquistimpuls mit Trapezspektrum für verschiedene Rolloff–Faktoren. Unten ist der entsprechende Zeitverlauf für das Cosinus–Rolloff–Spektrum dargestellt. Man erkennt:

Je kleiner der Rolloff–Faktor r ist, desto langsamer erfolgt der Abfall des Nyquistimpulses. Diese Aussage trifft sowohl für das Trapez– als auch für das Cosinus–Rolloff–Spektrum zu.
Im Grenzfall r → 0 ergibt sich in beiden Fällen das rechteckförmige Nyquistspektrum und der si–förmige Nyquistimpuls,</nobr> der asymptotisch mit 1/t abklingt (grüne Kurven).
Bei einem mittleren Rolloff (r ≈ 0.5) sind die ersten Überschwinger beim Trapezspektrum geringer als beim CRO–Spektrum, da bei gegebenem r die Nyquistflanke flacher verläuft (blaue Kurven).
Mit dem Rolloff–Faktor r = 1 wird im Frequenzbereich aus dem Trapez ein Dreieck und aus dem CRO–Spektrum das Cosinus–Quadrat–Spektrum (rote Kurven).
Mit r = 1 erfolgt der asymptotische Abfall der oberen Zeitfunktion (gemäß dem Trapezspektrum) mit 1/t² und der Abfall der unteren Zeitfunktion (gemäß dem CRO–Spektrum) mit 1/t³.

Zweites Nyquistkriterium (1)

Vor der exakten mathematischen Definition soll anhand von Grafiken veranschaulicht werden, welche Bedeutung das zweite Nyquistkriterium zur Bewertung eines Digitalsystems besitzt.

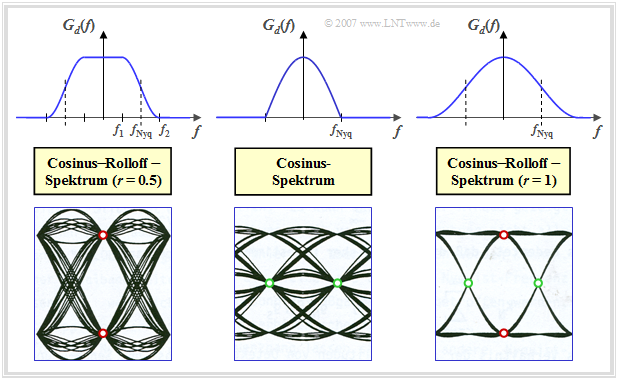
Die linke Grafik zeigt im Vorgriff auf das Kapitel 3.2 Please add link das Augendiagramm eines Nyquistsystems mit Cosinus–Rolloff–Charakteristik, wobei der Rolloff–Faktor r = 0.5 gewählt wurde. Da hier das erste Nyquistkriterium erfüllt ist (es besteht eine Punktsymmetrie um f_Nyq), ergibt sich für die vertikale Augenöffnung zum Zeitpunkt t = 0 der größtmögliche Wert 2 · g_d(0). Alle Augenlinien gehen zum Zeitpunkt t = 0 durch einen der beiden rot markierten Punkte.
Das mittlere Spektrum weist keine Symmetrie bezüglich des Flankenabfalls auf, so dass hier das erste Nyquistkriterium nicht erfüllt ist – im Gegensatz zum zweiten. Alle Augenlinien schneiden hier die Zeitachse zu den selben Zeiten (markiert durch die grünen Punkte), was beispielsweise die Taktwiedergewinnung mittels einer PLL (Phase-Locked Loop) erleichtert. Die horizontale Augenöffnung ist bei Erfüllung des zweiten Nyquistkriteriums maximal gleich der Symboldauer T.
Das rechte Augendiagrammm verdeutlicht, dass beim CRO–Spektrum mit r = 1 – und nur bei diesem – sowohl das erste als auch das zweite Nyquistkriterium erfüllt werden. Der Nyquistimpuls\[g_d ( t )= g_0 \cdot \frac{\pi }{4}\cdot {\rm si} \left ( \frac{\pi \cdot t}{T}\right)\cdot \left [ {\rm si}(\pi \cdot (\frac{t}{T} + \frac{1}{2}) + {\rm si}(\pi \cdot (\frac{t}{T} - \frac{1}{2})\right]\]

weist hier die erforderlichen Nulldurchgänge bei t = ±T, t = ±1.5T, t = ±2T, t = ±2.5T, ... auf, nicht jedoch bei ±0.5T. Die Impulsamplitude ist g_d(t = 0) = g₀.

Zweites Nyquistkriterium (2)

Ein Impuls g_Nyq-2(t), der das zweite Nyquistkriterium erfüllt, muss Nulldurchgänge bei ±1.5T, ±2.5T, ±3.5T, ... besitzen. Dagegen weist ein Nyquist–1–Impuls Nulldurchgänge bei ±T, ±2T, ±3T auf. Deshalb lässt sich ein Nyquist–2–Impuls immer als Summe zweier (eventuell unterschiedlicher) und um ±T/2 verschobener Nyquist–1–Impulse darstellen. Geht man von einem Impuls g_Nyq–1(t) aus, so gilt:\[g_{_{\rm Nyq-2}} ( t )= g_{_{\rm Nyq-1}} ( t +{T}/{2})+ g_{_{\rm Nyq-1}} ( t -{T}/{2})\hspace{0.05cm}.\] Im Frequenzbereich lautet das zweite Nyquistkriterium (siehe Söder, G.; Tröndle, K.: Digitale Übertragungssysteme - Theorie, Optimierung & Dimensionierung der Basisbandsysteme. Berlin – Heidelberg: Springer, 1985.):\[\sum_{k = -\infty}^{+\infty} \frac {G_d \left ( f - \frac{k}{T} \right)}{\cos(\pi \cdot f \cdot T - k \cdot \pi)}= {\rm const.}\]

: Ausgehend vom Impuls g(t) = g₀ · si(π · t/T), der das erste Nyquistkriterium erfüllt, lautet der dazugehörige Nyquist–2–Impuls:\[g_{_{\rm Nyq-2}}( t )& = & g_0 \cdot \left [ {\rm si}(\pi \cdot \frac{t + T/2}{T}) + {\rm si}(\pi \cdot \frac{t- T/2}{T}) \right] = \\ & = & \frac{2 \cdot g_0}{\pi} \cdot \frac{\cos(\pi \cdot t/T)}{1 - (2 \cdot t/T)^2}\hspace{0.05cm}.\]

Aufgrund der Begrenzung des Spektrums G_Nyq–1(f) auf den Bereich | f | ≤ f_Nyq = 1/(2T) beschränkt sich in obiger Gleichung die Summe auf den Term mit k = 0 und man erhält:\[G_{_{\rm Nyq-2}}(f) = \left\{ \begin{array}{c} g_0 \cdot T \cdot \cos(\frac{\pi \cdot f}{2 \cdot f_{_{\rm Nyq}}} )\\ \\ 0 \\\end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\hspace{0.15cm}|f| < f_{_{\rm Nyq}}\hspace{0.05cm}, \\ \\ {\rm{sonst}}\hspace{0.05cm}. \\ \end{array}\] Dieser Frequenzverlauf und das dazugehörige Augendiagramm ist in der Grafik auf der letzten Seite in der mittleren Spalte oben skizziert. Man erkennt deutlich die Erfüllung des zweiten Nyquistkriteriums.