Exercise 3.7Z: Regenerator Field Length
From LNTwww
Revision as of 15:17, 30 October 2017 by Hussain (talk | contribs) (Die Seite wurde neu angelegt: „{{quiz-Header|Buchseite=Digitalsignalübertragung/Lineare Nyquistentzerrung}} right|frame|Ergebnisse einer Systemsimulation…“)
Per Simulation wurde gezeigt, dass zwischen dem sog. Systemwirkungsgrad $\eta$ sowie der charakteristischen Kabeldämpfung $a_*$ eines Koaxialkabels – beide in dB aufgetragen – etwa ein linearer Zusammenhang besteht, wenn die charakteristische Kabeldämpfung hinreichend groß ist ($a_* ≥ 40 \ \rm dB$):
- $$10 \cdot {\rm lg}\hspace{0.1cm}\eta \hspace{0.15cm} {\rm (in \hspace{0.15cm}dB)}= A + B \cdot a_{\star} \hspace{0.05cm}.$$
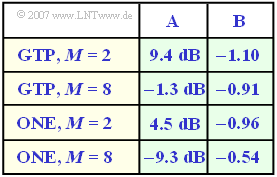
In der Tabelle sind für vier beispielhafte Systemvarianten
- impulsinterferenzbehaftetes System mit Gaußtiefpass (GTP, siehe Kapitel 3.4) bzw. optimale Nyquistentzerrung (ONE, siehe Kapitel 3.5)
- jeweils Binärsystem ($M = 2$) und Oktalsystem ($M = 8$)
die empirisch gefundenen Gleichungskoeffizienten $A$ und $B$ angegeben. Für einen gegebenen Wert $a_*$ (und damit eine feste Kabellänge) ist ein System um so besser, je größer der Systemwirkungsgrad ist.
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)