Exercise 1.5: HDB3 Coding
Der ISDN–Primärmultiplexanschluss basiert auf dem PCM–System $30/32$ und bietet $30$ vollduplexfähige Basiskanäle, dazu noch einen Signalisierungskanal sowie einen Synchronisationskanal.
Jeder dieser Kanäle, die im Zeitmultiplex übertragen werden, hat eine Datenrate von $64 \ \rm kbit/s$. Ein Rahmen besteht aus jeweils einem Byte ($8 \ \rm Bit$) aller $32$ Kanäle. Die Dauer eines solchen Rahmens wird mit $T_{\rm R}$ bezeichnet, während $T_{\rm B}$ die Bitdauer angibt.
Sowohl auf der $S_{\rm 2M}$– als auch auf der $U_{\rm K2}$–Schnittstelle des hier betrachteten ISDN–Systems wird der HDB3–Code verwendet, der vom AMI–Code abgeleitet ist. Es handelt sich hierbei um einen Pseudoternärcode ($M = 3$, Symboldauer $T = T_{\rm B}$), der sich vom AMI–Code in der Weise unterscheidet, dass lange Nullfolgen durch bewusste Verletzung der AMI–Codierregel vermieden werden. Dabei gilt:
- Treten im AMI–codierten Signal $a(t)$ vier aufeinander folgende „0”–Symbole auf, so werden diese durch vier andere Ternärsymbole ersetzt.
- Sind vor diesem Viererblock im Signal $a(t)$ eine gerade Anzahl von „+1” aufgetreten und der letzte Puls positiv (bzw. negativ), so wird „0 0 0 0” durch „– 0 0 –” (bzw. „+ 0 0 +”) ersetzt.
- Bei ungerader Anzahl von Einsen vor diesem „0 0 0 0”–Block werden dagegen als Ersetzungen „0 0 0 +” (falls letzter Puls positiv) oder „0 0 0 –” (falls letzter Puls negativ) gewählt.
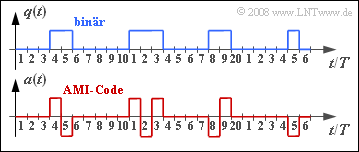
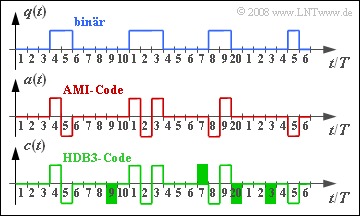
- Die Grafik zeigt oben das Binärsignal $q(t)$ und das Signal $a(t)$ nach der AMI–Codierung. Das HDB3–Signal, das Sie im Laufe dieser Aufgabe ermitteln sollen, wird mit $c(t)$ bezeichnet.
Hinweis:
- Die Aufgabe bezieht sich auf ISDN–Primärmultiplexanschluss dieses Buches.
- Weitere Informationen zu den Pseudoternärcodes finden Sie im Symbolweise Codierung mit Pseudoternärcodes von „Digitalsignalübertragung”.
Fragebogen
Musterlösung
(1) Die Gesamtdatenrate der insgesamt $32$ Kanäle zu je $64 \ \rm kbit/s$ ergibt $R_{\rm B} \underline{ = 2.048 \ \rm Mbit/s}$.
(2) Die Bitdauer ist $T_{\rm B} = 1/R_{\rm B} \underline{ = 0.488 \ \rm \mu s}$. Pro Rahmen wird jeweils ein Byte ($8 \ rm Bit$) eines jeden Kanals übertragen. Daraus folgt:
- $$T_{\rm R} = 32 \cdot 8 \cdot T_{\rm B} \hspace{0.15cm}\underline{= 125 \,{\rm \mu s}}\hspace{0.05cm}.$$
(3) Bis zum Zeitpunkt $t = 6T$ ist im AMI–codierten Signal $a(t)$ genau einmal eine „+1” aufgetreten. Wegen $a_{5} = –1$ wird beim HDB3–Code „0 0 0 0” durch
- $$\underline{c_{6} = 0, \hspace{0.2cm}c_{7} = 0, \hspace{0.2cm}c_{8} = 0, \hspace{0.2cm}c_{9} = -1} \hspace{0.05cm}$$
ersetzt, während $c_{10} = a_{10} = 0$ durch die HDB3–Codierung nicht verändert wird (siehe Grafik).
(4) Bis einschließlich $a_{13}$ gibt es dreimal ($\Rightarrow$ ungerade Anzahl) eine „+1”. Wegen $a_{12} = +1$ wird dieser Nullblock wie folgt ersetzt:
- $$ \underline{c_{14} = 0, \hspace{0.2cm}c_{15} = 0, \hspace{0.2cm}c_{16} = 0, \hspace{0.2cm}c_{17} = +1} \hspace{0.05cm}.$$
(5) Im AMI–codierten Signal tritt bis einschließlich $a_{19}$ genau viermal „+1” auf $\Rightarrow$ geradzahlige Anzahl. Da zudem $a_{19} = +1$ ist, lautet die Ersetzung entsprechend der Regel 2 auf der Angabenseite:
- $$\underline{c_{20} = -1, \hspace{0.2cm}c_{21} = 0, \hspace{0.2cm}c_{22} = 0, \hspace{0.2cm}c_{23} = -1} \hspace{0.05cm}.$$
Das Nullsymbol $a_{24}$ bleibt unverändert: $\underline{c_{24} = 0}$.