Contents
- 1 # ÜBERBLICK ZUM DRITTEN HAUPTKAPITEL #
- 2 Definition des Begriffs „Impulsinterferenz”
- 3 Mögliche Ursachen für Impulsinterferenzen
- 4 Einige Anmerkungen zum Kanalfrequenzgang
- 5 Frequenzgang eines Koaxialkabels
- 6 Impulsantwort eines Koaxialkabels
- 7 Voraussetzungen für das gesamte dritte Hauptkapitel
- 8 Aufgaben zum Kapitel
# ÜBERBLICK ZUM DRITTEN HAUPTKAPITEL #
Im Mittelpunkt des dritten Hauptkapitels stehen die Impulsinterferenzen, die beispielsweise durch Verzerrungen des Übertragungskanals entstehen oder mit einer von der Nyquistbedingung abweichenden Realisierung des Empfangsfilters zusammenhängen. Anschließend werden einige Entzerrungsverfahren beschrieben, mit denen die Systemdegradation durch Impulsinterferenzen abgemildert werden kann.
Die Beschreibung erfolgt durchgehend im Basisband. Die Ergebnisse lassen sich jedoch problemlos auch auf die im Kapitel Lineare digitale Modulation – Kohärente Demodulation behandelten Trägerfrequenzsysteme anwenden.
Im Einzelnen werden behandelt:
- die Ursachen und Auswirkungen von Impulsinterferenzen,
- das Augendiagramm als geeignetes Hilfsmittel zur Beschreibung von Impulsinterferenzen,
- die Fehlerwahrscheinlichkeitsberechnung unter Berücksichtigung von Kanalverzerrungen,
- der Einfluss von Impulsinterferenzen bei mehrstufiger und/oder codierter Übertragung,
- der optimale Nyquistentzerrer als Beispiel für lineare Kanalentzerrung,
- die Entscheidungsrückkopplung (DFE) – eine effektive nichtlineare Entscheiderrealisierung,
- der Korrelationsempfänger als Beispiel für Maximum–Likelihood– bzw. MAP–Entscheidung,
- der Viterbi–Empfänger, ein aufwandsreduzierter MAP–Entscheidungsalgorithmus.
Weitere Informationen zum Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im
- Versuch 3: Impulsinterferenzen und Entzerrung, Programm „bas”
des Praktikums „Simulation digitaler Übertragungssysteme”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf
- dem Lehrsoftwarepaket LNTsim ⇒ Link verweist auf die ZIP-Version des Programms und
- dieser Praktikumsanleitung ⇒ Link verweist auf die PDF-Version (76 Seiten).
Definition des Begriffs „Impulsinterferenz”
Für die beiden ersten Hauptkapitel dieses Buches wurde vorausgesetzt, dass der Detektionsgrundimpuls $g_d(t)$
- entweder auf den Zeitbereich $|t| \le T$ begrenzt ist, oder
- äquidistante Nulldurchgänge im Symbolabstand $T$ aufweist.
Bezeichnen wir die Abtastwerte von $g_d(t)$ bei Vielfachen der Symboldauer $T$ (Abstand der Impulse) als die Detektionsgrundimpulswerte, so wurde bisher stillschweigend vorausgesetzt:
- $$g_\nu = g_d(\nu T) = \left\{ \begin{array}{c} g_0 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c}\nu = 0, \\ \nu \ne 0. \\ \end{array}$$
Als Konsequenz dieser Annahme hat sich daraus ergeben, dass im binären Fall der Nutzanteil (Index „S”)
- $$d_{\rm S}(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g_d ( t - \nu \cdot T) \hspace{0.3cm}{\rm mit}\hspace{0.3cm}a_\nu \in \{ -1, +1\}$$
des Detektionssignals zu den Zeitpunkten $\nu \cdot T$ nur zwei verschiedene Werte annehmen kann, nämlich $\pm g_0$.
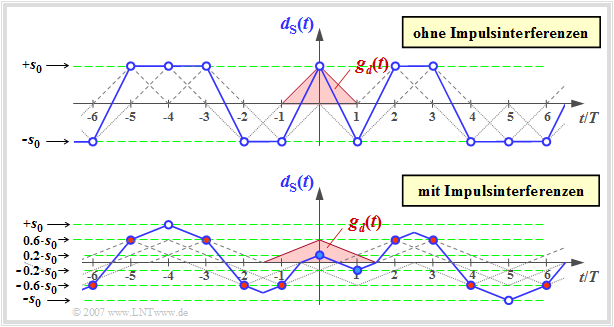
- Das obere der beiden Zeitdiagrammen zeigt $d_{\rm S}(t)$ für diesen impulsinterferenzfreien Fall mit $g_{\nu \ne 0} = 0$ und $g_0 = s_0$ ⇒ der Grundimpulshauptwert $g_0$ ist gleich dem Maximalwert $s_0$ des Sendesignals.
- Darunter gezeichnet ist der Signalverlauf für einen Satz von Detektionsgrundimpulswerten, die Impulsinterferenzen hervorrufen:
- $$g_0 = 0.6 \cdot s_0, \hspace{0.2cm}g_{-1} = g_{+1} =0.2 \cdot s_0, \hspace{0.2cm}g_\nu =0\hspace{0.3cm}{\rm f\ddot{u}r}\hspace{0.3cm} |\nu| \ge 2 \hspace{0.05cm}.$$
In beiden Darstellungen ist der (jeweils dreieckförmige) Detektionsgrundimpuls $g_d(t)$ rot eingezeichnet. Die Detektionszeitpunkte $\nu \cdot T$ sind jeweils durch blaue Kreise markiert. Man erkennt aus dem unteren Signalverlauf :
- Der Detektionsgrundimpuls $g_d(t)$ ist nun im Bereich $|t| \le 1.5 \cdot T$ von Null verschieden und erfüllt somit nicht mehr die Nyquist–Bedingung (im Zeitbereich) für Impulsinterferenzfreiheit.
- Dies hat zur Folge, dass zu den (mit Kreisen markierten) Detektionszeitpunkten nicht nur zwei Werte $(\pm s_0)$ möglich sind wie im oberen Bild. Vielmehr gilt für die Detektionsnutzabtastwerte:
- $$d_{\rm S}(\nu \cdot T) \in \{ \pm s_0, \ \pm 0.6 s_0, \ \pm 0.2 s_0\}\hspace{0.05cm}.$$
- Die Abtastwerte, die aufgrund ungünstiger Nachbarimpulse nahe an der Schwelle liegen, werden durch das AWGN–Rauschen (mit Rauscheffektivwert $\sigma_d$) häufiger verfälscht als die weiter außen liegenden Abtastwerte.
- Beispielhaft werden mit $\sigma_d = 0.2 \cdot s_0$ die blau ausgefüllten Punkte nahe der Schwelle mit großer Wahrscheinlichkeit $p_{\rm S} ={\rm Q} (1) \approx 16 \%$ verfälscht und die äußeren Punkte (mit weißem Kern) nur mit $p_{\rm S} ={\rm Q} (5) \approx 3 \cdot 10^{-7}$. Die Fehlerwahrscheinlichkeit der rot gefüllten Punkte (alle im Abstand $0.6 \cdot s_0$ von der Null–Linie) liegt dazwischen: $p_{\rm S} ={\rm Q} (3) \approx 0.13 \%$ .
Bisher wurden die Auswirkungen von Impulsinterferenzen möglichst anschaulich dargelegt. Es fehlt noch eine exakte Begriffsbestimmung.
$\text{Definition:}$ Unter Impulsinterferenz (englisch: Intersymbol Interference, ISI) versteht man die Beeinträchtigung einer Symbolentscheidung aufgrund einer Impulsverbreiterung (Zeitdispersion) und damit verbunden eine Abhängigkeit der Fehlerwahrscheinlichkeit von den Nachbarsymbolen.
In anderen Worten:
- Durch abfallende Flanken vorangegangener Impulse („Nachläufer”) und ansteigende Flanken nachfolgender Impulse („Vorläufer”) wird der momentan anliegende Detektionsabtastwert verändert.
- Dadurch kann die Wahrscheinlichkeit einer Fehlentscheidung für das aktuelle Symbol vergrößert oder verkleinert werden, je nachdem, ob der Abstand zur Schwelle kleiner oder größer wird.
- Im statistischen Mittel – also bei Betrachtung einer (unendlich) langen Symbolfolge – führt dies stets zu einer (beträchtlichen) Erhöhung der (mittleren) Symbolfehlerwahrscheinlichkeit $p_{\rm S} $.
Mögliche Ursachen für Impulsinterferenzen
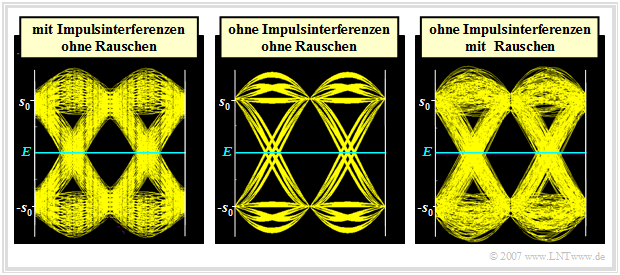
Die folgende Grafik zeigt das Augendiagramm für ein
- impulsinterferenzbehaftetes System ohne Rauschen (links),
- ein impulsinterferenzfreies System ohne Rauschen (Mitte),
- das gleiche impulsinterferenzfreie System mit Rauschen (rechts).
Auf die Definition, Bedeutung und Berechnung des Augendiagramms wird im Kapitel Fehlerwahrscheinlichkeit unter Berücksichtigung von Impulsinterferenzen noch ausführlich eingegangen. Die Grafiken wurden mit dem Programm „bas” erzeugt. Hinweis zum Download dieses Programms finden Sie am Beginn dieses Kapitels.
Diese Bilder können wie folgt interpretiert werden:
- Das mittlere Diagramm stammt von einem Nyquistsystem mit Cosinus–Rolloff–Charakteristik (Rolloff–Faktor $r = 0.5$). Es treten somit keine Impulsinterferenzen auf.
- Auch das rechte Augendiagramm stammt von einem impulsinterferenzfreien System (genauer gesagt: vom gleichen System wie die mittlere Grafik), obwohl hier $d(t) = \pm s_0$ nicht zutrifft. Die Abweichungen von den Sollwerten $\pm s_0$ sind hier auf das AWGN–Rauschen zurückzuführen.
- Aus diesem letzten Punkt folgt die wichtige Erkenntnis: Die Frage, ob ein impulsinterferenzfreies oder ein impulsinterferenzbehaftetes System vorliegt, kann nur anhand des Detektionssignals (bzw. des Augendiagramms) ohne Rauschen entschieden werden.
- Das linke Diagramm weist auf Impulsinterferenzen hin, da hier kein Rauschen berücksichtigt ist. Grund dieser Impulsinterferenzen könnte sein, dass der Gesamtfrequenzgang von Sender und Empfänger das erste Nyquistkriterium aufgrund von Toleranzen nicht exakt erfüllt.
- Impulsinterferenzen entstehen aber auch bei einem Kanal mit frequenzabhängigem Frequenzgang $H_{\rm K}(f)$, wenn es dem Empfänger nicht gelingt, die Dämpfungs– und Phasenverzerrungen des Kanals vollständig (also hundertprozentig) zu kompensieren.
- Letztendlich kommt es auch beim mittleren System zu Impulsinterferenzen, wenn nicht exakt in Augenmitte entschieden wird, sondern zu einem Detektionszeitpunkt $T_{\rm D} \ne 0$. Dann müssen die Detektionsgrundimpulswerte zu $g_\nu = g_d(T_{\rm D} + \nu \cdot T)$ definiert werden.
Einige Anmerkungen zum Kanalfrequenzgang
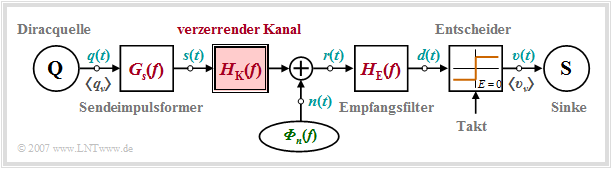
Für die weiteren Abschnitte in diesem dritten Hauptkapitel wird (meist) von folgendem Blockschaltbild ausgegangen. Der wesentliche Unterschied gegenüber dem Blockschaltbild zum Hauptkapitel 1 ist der Kanalfrequenzgang $H_{\rm K}(f)$, der bisher stets als ideal ⇒ $H_{\rm K}(f) = 1$ vorausgesetzt wurde.
Im Folgenden gelte für den Frequenzgang und die Impulsantwort des Kanals ($\rm exp[ . ]$ bezeichnet die Exponentialfunktion):
- $$H_{\rm K}(f) = {\rm exp} \left[ - a_{{\star} \hspace{0.01cm}({\rm Np})} \cdot \sqrt{\frac{f}{R_{\rm B}/2}}\hspace{0.1cm}\right] \cdot {\rm exp} \left[ - {\rm j} \cdot a_{{\star} \hspace{0.01cm}({\rm Np})} \cdot \sqrt{\frac{f}{R_{\rm B}/2}}\hspace{0.1cm}\right] \hspace{0.05cm}, $$
- $$h_{\rm K}(t) = \frac{ a_{{\star}\hspace{0.01cm}({\rm Np})}}{ \sqrt{2 \pi^2 \cdot R_{\rm B} \cdot t^3}}\hspace{0.1cm} \cdot {\rm exp} \left[ - \frac{a_{{\star} \hspace{0.01cm}({\rm Np})}^2}{2 \pi \cdot R_{\rm B} \cdot t}\hspace{0.1cm}\right] \hspace{0.05cm}.$$
Hierbei gibt $a_{{\star} \hspace{0.01cm}({\rm Np})}$ die Kabeldämpfung bei der halben Bitrate ⇒ charakteristische Kabeldämpfung in Neper (Np) an:
- $$a_{{\star} \hspace{0.01cm}({\rm Np})} = a_{\rm K}(f = {R_{\rm B}}/{2})= 0.1151 \cdot a_{{\star} \hspace{0.01cm}({\rm dB})} \hspace{0.05cm}.$$
Der entsprechende dB–Wert ist um den Faktor $1/0.1151 = 8.686$ größer. Bei realisierten Systemen liegt die charakteristische Kabeldämpfung $a_{{\star} \hspace{0.01cm}({\rm dB})}$ im Bereich zwischen $40 \ \rm dB$ und $100 \ \rm dB$. Auf den Zusatz „(Np)” bzw. „(dB)” wird im Folgenden meist verzichtet.
Im Hauptkapitel 4: „Eigenschaften elektrischer Leitungen” des Buches Lineare zeitinvariante Systeme wird gezeigt, dass diese Gleichungen die Verhältnisse bei leitungsgebundener Übertragung über Koaxialkabel mit guter Näherung wiedergeben. Bei einer Zweidrahtleitung ist die Abweichung zwischen dieser sehr einfachen, analytisch handhabbaren Formel und den tatsächlichen Gegebenheiten etwas größer.
Eine kurze Zusammenfassung dieser Herleitungen folgt auf den beiden nächsten Seiten, wobei wir uns zur Vereinfachung auf ein redundanzfreies Binärsystem festlegen. Somit ist die Bitrate $R_{\rm B}$ gleich dem Kehrwert der Symboldauer $T$.
Frequenzgang eines Koaxialkabels
Ein Koaxialkabel mit dem Kerndurchmesser 2.6 mm, dem Außendurchmesser 9.5 mm und der Länge $l$ hat den folgenden Frequenzgang:
- $$H_{\rm K}(f) = {\rm e}^{-[ a_{\rm K}(f) + {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} b_{\rm K}(f)] } = {\rm e}^{- \alpha_0 \hspace{0.05cm} \cdot \hspace{0.05cm} l} \cdot {\rm e}^{- (\alpha_1 + {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \beta_1) \hspace{0.05cm}\cdot f \hspace{0.05cm}\cdot \hspace{0.05cm}l} \cdot {\rm e}^{- (\alpha_2 + {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \beta_2) \hspace{0.05cm}\cdot \sqrt{f} \hspace{0.05cm}\cdot \hspace{0.05cm}l} \hspace{0.05cm},$$
wobei bei diesen Abmessungen – man spricht vom Normalkoaxialkabel – folgende Parameter gelten:
- $$\alpha_0 = 0.00162 \hspace{0.15cm}\frac {\rm Np}{\rm km} \hspace{0.05cm},\hspace{0.2cm} \alpha_1 = 0.000435 \hspace{0.15cm}\frac {\rm Np}{{\rm km} \cdot {\rm MHz}} \hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 0.2722 \hspace{0.15cm}\frac {\rm Np}{{\rm km} \cdot \sqrt{\rm MHz}} \hspace{0.05cm},\hspace{0.2cm} \beta_1 = 21.78 \hspace{0.15cm}\frac {\rm rad}{{\rm km} \cdot {\rm MHz}} \hspace{0.05cm}, \hspace{0.2cm} \beta_2 = 0.2722 \hspace{0.15cm}\frac {\rm rad}{{\rm km} \cdot \sqrt{\rm MHz}} \hspace{0.05cm}.$$
In obiger Gleichung sind die Dämpfungsparameter in „Np” einzusetzen und die Phasenparameter in „rad”.
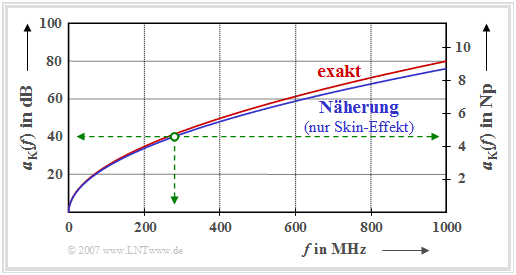
Die Grafik zeigt den exakten Dämpfungsverlauf und eine Näherung
- $$a_{\rm K}(f) = \alpha_0 \cdot l \hspace{0.05cm} + \hspace{0.05cm} \alpha_1 \cdot f \cdot l + \hspace{0.05cm} \alpha_2 \cdot \sqrt{f} \cdot l \hspace{0.05cm},$$
- $$a_{\rm K}(f) \approx \alpha_2 \cdot \sqrt{f} \cdot l$$
für ein Normalkoaxialkabel von einem Kilometer Länge für Frequenzen bis $f = 1000\ \rm MHz$.
- Die Achse ist links in $\rm dB$ und rechts in $\rm Np$ beschriftet.
- Ein $\rm Np$ (Neper) entspricht $8.686 \ \rm dB$.
Wir verweisen an dieser Stelle auf das interaktive Applet Dämpfung von Kupferkabeln.
Man erkennt aus dem Diagramm und obigen Zahlenwerten:
- Der von den Ohmschen Verlusten herrührende erste Term $(\alpha_0 \cdot l)$ ist vernachlässigbar. Zudem bewirkt dieser Term nur eine frequenzunabhängige Dämpfung und keine Signalverzerrung.
- Der auf die Querverluste zurückzuführende zweite Term $(\alpha_1 \cdot f \cdot l)$ ist proportional zur Frequenz und macht sich daher erst bei sehr hohen Frequenzen bemerkbar; er wird im Folgenden vernachlässigt.
- Die frequenzproportionale Phase $(\beta_1 \cdot f \cdot l)$ hat nur eine Signalverzögerung um die Laufzeit $\beta_1/(2\pi) \cdot l$ zur Folge, jedoch keine Verzerrung. Auch diese Laufzeit wird im Folgenden außer Acht gelassen.
- Mit diesen Vereinfachungen wird somit der Frequenzgang allein durch den Skineffekt bestimmt. Da die Zahlenwerte für $\alpha_2$ (in Np) und $\beta_2$ (in rad) übereinstimmen, gilt somit auch:
- $$H_{\rm K}(f) ={\rm e}^{- (\alpha_2 + {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \beta_2) \hspace{0.05cm}\cdot \sqrt{f} \hspace{0.05cm}\cdot \hspace{0.05cm}l} \cdot {\rm e}^{- \alpha_2 \hspace{0.05cm}\cdot \hspace{0.05cm}l \hspace{0.05cm}\cdot \sqrt{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2f}} \hspace{0.05cm}.$$
- Häufig wird in der Literatur – und auch in diesem Tutorial – das Dämpfungsmaß bei der halben Bitrate benutzt, das wir als charakteristische Kabeldämpfung (in Neper) bezeichnen:
- $$a_{\star} = a_{\rm K}(f ={R_{\rm B}}/{2})= a_{\rm K}(f = \frac{1}{2 \cdot T})\approx \frac{\alpha_2 \cdot l }{ \sqrt {2\cdot T}} \hspace{0.05cm}.$$
$\text{Beispiel 1:}$ Bei einem Binärsystem mit der halben Bitrate $R_{\rm B}/2 = 280 \ \rm Mbit/s$ und $l = 1\ \rm km$ ergibt sich $a_{\star} \approx 4.55 \ \rm Np$ bzw. $a_{\star} \approx 40 \ \rm dB$ (grün eingezeichnete Markierungen in obiger Grafik).
Beträgt aber die halbe Bitrate nur $70 \ \rm Mbit/s$, so charakterisiert $a_{\star} = 40 \ \rm dB$ ein Übertragungssystem mit der Kabellänge $l = 2\ \rm km$.
Bereits an dieser Stelle soll darauf hingewiesen werden, dass die obige Näherung $a_{\rm K}(f) \approx \alpha_2 \cdot \sqrt{f} \cdot l$ nur für Koaxialkabel zulässig ist, da bei diesen die Koeffizienten $\alpha_0$und $\alpha_1$ vernachlässigt werden können.
Für eine symmetrische Zweidrahtleitung sind die Koeffizienten $\alpha_0$und $\alpha_1$ sehr viel gößer und obige Näherung ist unzulässig.
Impulsantwort eines Koaxialkabels
Wir etrachten wir nun die Koaxialkabel–Impulsantwort, die bei einem Binärsystem $(R_{\rm B} = 1/T)$ wie folgt lautet:
- $$h_{\rm K}(t) = \frac{ a_{\rm \star \hspace{0.01cm}(Np)}/T}{ \sqrt{2 \pi^2 \cdot (t/T)^3}}\hspace{0.1cm} \cdot {\rm exp} \left[ - \frac{a_{\rm \star \hspace{0.01cm}(Np)}^2}{2 \pi \cdot t/T}\hspace{0.1cm}\right] \hspace{0.05cm}.$$
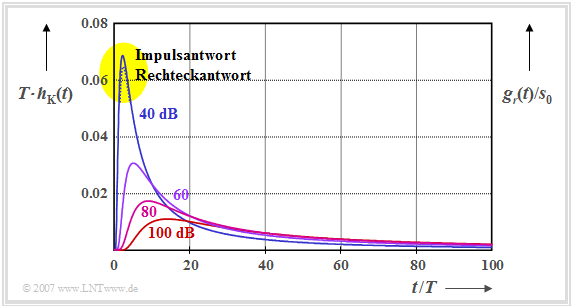
Dieser Zeitverlauf ist hier für charakteristische Kabeldämpfungen $(a_{\rm \star})$ zwischen $40 \ \rm dB$ und $100 \ \rm dB$ dargestellt. Beachten Sie die Umrechnung $\rm 1 \ Np = 8.686 \ dB.$
Man erkennt aus dieser Zeitbereichsdarstellung:
- Bereits mit der relativ kleinen charakteristischen Kabeldämpfung $a_{\rm \star} = 40 \ \rm dB$ erstreckt sich die Impulsantwort über mehr als $100$ Symboldauern $(T)$.
- Je größer $a_{\rm \star}$ gewählt wird, desto breiter und niedriger wird die Impulsantwort. Das Integral über $h_{\rm K}(t)$ von Null bis Unendlich ist für alle Kurven gleich, da stets $H_{\rm K}(f=0) = 1$ gilt.
- Der Empfangsgrundimpuls $g_r(t) = g_s(t) \star h_{\rm K}(t)$ ist nahezu formgleich mit $h_{\rm K}(t)$. Die rechte Ordinatenachse zeigt $g_r(t)/s_0$, wenn $g_s(t)$ ein NRZ–Rechteckimpuls mit Höhe $s_0$ und Dauer $T$ ist.
- Für $a_{\rm \star} \ge 60 \ \rm dB$ sind $h_{\rm K}(t)$ und $g_r(t)$ bei geeigneter Normierung innerhalb der Zeichengenauigkeit nicht zu unterscheiden. Für $a_{\rm \star} = 40 \ \rm dB$ erkennt man eine kleine Differenz an der Spitze (gelbe Hinterlegung); $g_r(t)/s_0$ ist hier minimal kleiner als $T \cdot h_{\rm K}(t)$.
- Mit der charakteristischen Dämpfung $a_{\rm \star} = 40 \ \rm dB$ beträgt die Impulsamplitude am Kabelende allerdings weniger als $7\%$ der Eingangsamplitude. Bei $60 \ \rm dB$ bzw. $100 \ \rm dB$ sinkt dieser Wert auf $3\%$ bzw. $2\%$.
In der Aufgabe 3.1 wird die Koaxialkabel–Impulsantwort
eingehend analysiert. Wir verweisen hier auch auf das interaktive Applet Zeitverhalten von Kupferkabeln.
Voraussetzungen für das gesamte dritte Hauptkapitel
Betrachten wir nochmals das Blockschaltbild eines Übertragungssystems, wobei wir einen stark verzerrendem Kanal voraussetzen, wie er beispielsweise bei leitungsgebundener Übertragung vorliegt.
Aufgrund des in der Grafik rot hervorgehobenen Kanalfrequenzgangs $H_{\rm K}(f)$ ergeben sich auch für die anderen Systemkomponenten gewisse Einschränkungen:
- Der Empfangsgrundimpuls $g_r(t) = g_s(t) \star h_{\rm K}(t)$ erstreckt sich über Hunderte von Bits (siehe letzte Seite). Deshalb kann das Empfangsfilter $H_{\rm E}(f)$ nicht als Matched–Filter angesetzt werden, da so die Dauer des Detektionsgrundimpulses $g_d(t)$ gegenüber $g_r(t)$ nochmals etwa verdoppelt würde.
- Vielmehr muss $H_{\rm E}(f)$ die enormen Dämpfungsverzerrungen ($\alpha_2$–Term) und Phasenverzerrungen ($\beta_2$–Term) des koaxialen Kanals $H_{\rm E}(f)$ kompensieren, insbesondere dann, wenn von einem einfachen Schwellenwertentscheider ausgegangen wird.
- Diese lineare Form der Signalentzerrung kann zwar durch aufwändigere Entscheiderstrategien – zum Beispiel Entscheidungsrückkopplung, Korrelationsempfänger oder Viterbi–Empfänger – unterstützt werden. Bei leitungsgebundener Übertragung kann aber aufgrund der sehr starken Verzerrungen auf eine lineare Signalentzerrung ⇒ entzerrendes Empfangsfilter $H_{\rm E}(f)$ nicht vollständig verzichtet werden.
- Das Rauschen $n(t)$ wird weiterhin als additiv, weiß und gaußverteilt (AWGN) angesetzt, was bei einem Koaxialkabel gerechtfertigt ist. Bei einer Zweidrahtleitung ist das Nebensprechen von benachbarten Kupferadern die dominante Störung, wie im Kapitel ISDN (Integrated Services Digital Network) im Buch „Beispiele von Nachrichtensystemen” ausführlich dargelegt wird.
$\text{Fazit:}$ Wir betrachten in den folgenden Kapiteln die binäre bipolare redundanzfreie Übertragung, wobei die Bitrate $R_{\rm B} = 1/T$ beträgt. Dabei wird stets vorausgesetzt:
- Der Sendegrundimpuls $g_s(t)$ ist NRZ–rechteckförmig mit Amplitude $s_0$ und Dauer $T$. Somit ist das Sendesignal $s(t)$ zu allen Zeiten gleich $\pm s_0$ und die Spektralfunktion lautet: $G_s(f) = s_0 \cdot T \cdot {\rm si}(\pi f T)$.
- Eine Aufteilung der Entzerrung auf Sender und Empfänger entsprechend der Wurzel–Wurzel–Charakteristik macht bei leitungsgebundener Übertragung keinen Sinn. Es würden bereits beim Sender zu starke Impulsinterferenzen auftreten.
Aufgaben zum Kapitel
Aufgabe 3.1: Impulsantwort des Koaxialkabels
Aufgabe 3.1Z: Frequenzgang des Koaxialkabels