Exercise 3.10: Rayleigh Fading

Zur Rayleigh-WDF

Häufig beschreibt man ein Bandpassübertragungssystem im sogenannten äquivalenten Tiefpassbereich. Diese Darstellung führt entsprechend dem Kapitel „Bandpassartige Signale” im Buch Signaldarstellung zu einem komplexen Signal:

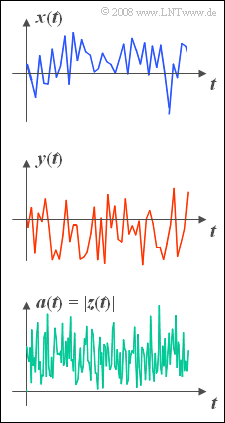
$$z(t)=x(t)+ {\rm j} \cdot y(t).$$

Der Realteil $x(t)$ kennzeichnet hierbei die Inphasekomponente und der Imaginärteil $y(t)$ die Quadraturkomponente.

Bei einem Mobilfunksystem, bei dem zwischen dem mobilen Teilnehmer und der Basisstation keine Sichtverbindung besteht, gelangt somit das Funksignal ausschließlich auf indirekten Wegen (Brechung, Streuung, Reflexion usw.) zum Empfänger. In diesem Fall ist folgendes Modell anwendbar:

Der Realteil $x(t)$ und auch der Imaginärteil $y(t)$ sind jeweils gaußverteilt und mittelwertfrei.
$x(t)$ und $y(t)$ besitzen jeweils die gleiche Streuung $\sigma$ und sind voneinander unabhängig.
Innere Bindungen der Signale $x(t)$ und $y(t)$ aufgrund des Dopplereffekts sollen hier nicht beachtet werden.

Das komplexe Signal $z(t)$ kann man auch nach Betrag und Phase darstellen:

$$ z(t)= a(t)\cdot {\rm e}^{{\rm j} \phi(t)}.$$

Aufgrund der Symmetrie bezüglich $x(t)$ und $y(t)$ ist die Phase $\phi(t)$ gleichverteilt.
Dagegen ist der Betrag $a(t) = |z(t)|$ rayleighverteilt, was zu der Namensgebung „Rayleighfading” geführt hat.
Als weitere Größe definieren wir noch die Momentanleistung

$$ p(t)=x^{\rm 2}(t)+y^{\rm 2}( t)=a^{\rm 2}(t).$$

Die Zufallsgröße $p$ ist hier (einseitig) exponentialverteilt. Deren WDF lautet für $p>0$:

$$f_p(p)=\frac{1}{2\sigma^{\rm 2}}\cdot {\rm e}^{ -p/(\sigma^{\rm 2})}.$$

Für alle negativen $p$–Werte gilt natürlich $f_p(p)= 0$, da $p$ eine Leistung kennzeichnet.

Hinweise:

Die Aufgabe gehört zum Kapitel Weitere Verteilungen.
Insbesondere wird Bezug genommen auf die Seite Rayleighverteilung.
Die Streuungen der beiden Gaußschen Zufallsgrößen $x$ und $y$ seien jeweils $\sigma = 1$.
Alle Größen sind deshalb als normiert zu verstehen.

Fragebogen

	Kleine Momentanleistungen sind wahrscheinlicher als große.
	Die Phase $\phi(t) = \pi/2$ bedeutet auch „Imaginärteil $y(t) = 0$”.
	Die Phase $\phi(t) = -\pi/2$ bedeutet auch „Realteil $x(t) = 0$”.

${\rm Pr}(p(t) > 4) \ = \ $

${\rm Pr}(a(t) > 2) \ = \ $

$f_a(a = 1)\ = \ $

Musterlösung

Solution

(1) Richtig sind der erste und der dritte Lösungsvorschlag:

Die erste Aussage trifft aufgrund der Exponentialverteilung für $p(t)$ zu.
Ein Phasenwinkel $\phi(t) = \pm \pi/2 (\pm 90^\circ)$ bedeutet, dass der Realteil $x(t) = 0$ ist.
Bei positivem Imaginärteil ⇒ $y(t) > 0$ ist der Phasenwinkel $\phi(t) = +90^\circ$, bei negativem Imaginärteil beträgt der Phasenwinkel $\phi(t) = -90^\circ$.

(2) Mit $\sigma = 1$ gilt für die WDF der Momentanleistung:

$$f_p(p)= {\rm 1}/{\rm 2}\cdot{\rm e}^{-p/\rm 2}.$$

Die gesuchte Wahrscheinlichkeit ist demnach:

$${\rm Pr}(p(t) > 4) = \int_{\rm 4}^{\infty}{1}/{2}\cdot{\rm e}^{-p/\rm 2}\,{\rm d} p={\rm e}^{\rm -2} \rm \hspace{0.15cm}\underline{=0.135}.$$

(3) Da $p(t) =a^2(t)$ gilt und zudem $a(t) < 0$ nicht möglich ist, ist das Ereignis $a(t) > 2$ identisch mit dem Ereignis $p(t) > 4$.

Es ergibt sich die gleiche Wahrscheinlichkeit ${\rm Pr}(a(t) > 2) \hspace{0.15cm}\underline{=0.135}$ wie unter (2) berechnet.

(4) Allgemein gilt:

$$f_a(a)=\frac{f_p(p)}{|g'(p)|}\Bigg |_{\, p=h(a)}.$$

Die Transformationskennlinie lautet:

$$g\hspace{0.05cm}'(p)=\frac{ {\rm d} a}{ {\rm d} p}=\frac{1}{2 \cdot \sqrt{p}}.$$

Diese ist stets positiv. Daraus folgt für die Rayleigh–WDF:

$$f_a(a)=\sqrt {p}\cdot {\rm e}^{ -p/\rm 2}\Big|_{ p=a^{\rm 2}}= a\cdot {\rm e}^{\, -a^{\rm 2}/\rm 2}.$$

Für $a = 1$ ergibt sich somit der Wert $f_a(a = 1)= {\rm e}^{-0.5}\hspace{0.15cm}\underline{=0.607} $.