Examples of Binary Block Codes

Single Parity–check Codes

Der Single Parity–check Code (SPC) fügt zu dem Informationsblock $\underline{u}= (u_1, u_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, u_k)$ ein Prüfbit (englisch: Parity ) $p$ hinzu:

Verschiedene Single Parity–check Codes $(n = k + 1)$

$$\underline{u} = (u_1, u_2,\hspace{0.05cm} \text{...} \hspace{0.05cm} , u_k) \hspace{0.3cm}$$

$$\Rightarrow \hspace{0.3cm} \underline{x} = (x_1, x_2,\hspace{0.05cm}\text{...} \hspace{0.05cm} , x_n) = (u_1, u_2,\hspace{0.05cm} \text{...}\hspace{0.05cm} , u_k, p) \hspace{0.05cm}.$$

Die Grafik zeigt drei Coder–Beispiele mit

$|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 4 \ (k = 2)$,

$|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 8 \ (k = 3)$,

$|\hspace{0.05cm}\mathcal{C}\hspace{0.05cm}| = 16 \ (k = 4)$.

Dieser sehr einfache Code kann wie folgt charakterisiert werden:

Aus $n = k + 1$ folgt für die Coderate $R = k/n = (n-1)/n$ und für die Redundanz $1-R = 1/n$. Für $k = 2$ ergibt sich zum Beispiel die Coderate $2/3$ und die relative Redundanz beträgt $33.3\%$.

Das Prüfbit erhält man durch die Modulo–2–Addition. Darunter versteht man die Addition im Galoisfeld zur Basis $2$ ⇒ $\rm GF(2)$, sodass $1 \oplus 1 = 0$ ergibt:

\[p = u_1 \oplus u_2 \oplus \text{...} \hspace{0.05cm} \oplus u_k \hspace{0.05cm}.\]

Damit enthält jedes gültige Codewort $\underline{x}$ eine gerade Anzahl von Einsen. Ausgedrückt mit $\oplus$ bzw. in vereinfachter Schreibweise gemäß der zweiten Gleichung lautet diese Bedingung:

\[ x_1 \oplus x_2 \oplus \text{...} \hspace{0.05cm} \oplus x_n = 0 \hspace{0.05cm}, \hspace{0.5cm}{\rm oder:}\hspace{0.5cm} \sum_{i=1}^{n} \hspace{0.2cm} x_i = 0\hspace{0.05cm} , \hspace{0.3cm} {\rm Addition\hspace{0.15cm} in \hspace{0.15cm} GF(2)} \hspace{0.05cm}. \]

Für $k = 2$ ⇒ $n = 3$ ergeben sich die folgenden vier Codeworte, wobei das Prüfbit $p$ jeweils durch einen kleinen Pfeil markiert ist:

\[\underline{x}_0 = (0, 0_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_1 = (0, 1_{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_2 = (1, 0 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 1)\hspace{0.05cm}, \hspace{0.2cm} \underline{x}_3 = (1, 1 _{\hspace{0.05cm} \rightarrow}\hspace{0.05cm} 0)\hspace{0.05cm}.\]

Dieser Code $\mathcal{C} = \big \{ (0, 0, 0), \ (0, 1, 1), \ (1, 0, 1), \ (1, 1, 0) \big \}$ ist linear, da die Summe zweier beliebiger Codeworte wieder ein gültiges Codewort ergibt, zum Beispiel

$$\underline{x}_1 \oplus \underline{x}_2 = \underline{x}_3.$$

Für beliebiges $k$ ⇒ $n = k+1$ unterscheidet sich jedes Codewort von allen anderen an einer geraden Anzahl von Positionen. Die minimale Distanz des Codes ist also

$$d_{\rm min} = 2.$$

$\text{Definition:}$ Jeder $\text{Single Parity–check Code (SPC)}$ lässt sich formal wie folgt beschreiben:

\[\mathcal{C} = \{ \underline{x} \in {\rm GF}(2^n)\hspace{-0.15cm}: \hspace{0.15cm}{\rm mit \hspace{0.15cm}geradzahliger\hspace{0.15cm} Anzahl\hspace{0.15cm} von\hspace{0.15cm} Einsen\hspace{0.15cm} in \hspace{0.15cm} } \underline{x} \}\hspace{0.05cm}.\]

Mit der allgemeinen Codebezeichnung $(n, \ k, \ d_{\rm min})$ lässt sich jeder Single Parity–check Code auch mit $\text{SPC }(n, \ n-1, \ 2)$ benennen.
Die obere Grafik zeigt somit den $\text{SPC (3, 2, 2)}$, den $\text{SPC (4, 3, 2)}$ und den $\text{SPC (5, 4, 2)}$.

Der digitale Kanal ändert möglicherweise das Codewort $\underline{x}= (x_1, x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, x_n)$ in das Empfangswort $\underline{y}= (y_1, y_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, y_n)$. Mit dem Fehlervektor $\underline{e}= (e_1, e_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, e_n)$ gilt:

$$\underline{y}= \underline{x} \oplus \underline{e}.$$

Zur Decodierung des Single Parity–check Codes bildet man das so genannte Syndrom:

\[s = y_1 \oplus y_2 \oplus \hspace{0.05cm}\text{...} \hspace{0.05cm} \oplus y_n = \sum_{i=1}^{n} \hspace{0.2cm} y_i \hspace{0.1cm} \in \hspace{0.2cm} \{0, 1 \} \hspace{0.05cm}.\]

Das Ergebnis $s=1$ weist dann auf (mindestens) einen Bitfehler innerhalb des Codewortes hin, während $s=0$ wie folgt zu interpretieren ist:

Die Übertragung war fehlerfrei, oder:
Die Anzahl der Bitfehler ist geradzahlig.

Mögliche Empfangswerte beim $\text{SPC (4, 3, 2)}$

$\text{Beispiel 1:}$ Wir betrachten den $\text{SPC (4, 3, 2)}$ und gehen davon aus, dass das Nullwort gesendet wurde. Die Tabelle zeigt alle Möglichkeiten, dass $f$ Bit verfälscht werden und gibt das jeweilige Syndrom $s \in \{0, 1\}$ an.

Für das BSC–Modell mit der Verfälschungswahrscheinlichkeit $\varepsilon = 1\%$ ergeben sich dann folgende Wahrscheinlichkeiten:

Das Informationswort wird richtig decodiert (blaue Hinterlegung):

\[{\rm Pr}(\underline{v} = \underline{u}) = {\rm Pr}(\underline{y} = \underline{x}) = (1 - \varepsilon)^n = 0.99^4 \approx 96\,\%\hspace{0.05cm}.\]

Der Decoder erkennt, dass Übertragungsfehler aufgetreten sind (grüne Hinterlegung):

\[{\rm Pr}(s=1) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=1 \atop f \hspace{0.1cm}{\rm ungerade} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} = {4 \choose 1} \cdot 0.01 \cdot 0.99^3 + {4 \choose 3} \cdot 0.01^3 \cdot 0.99 \approx 3.9\,\%\hspace{0.05cm}.\]

Das Informationswort wird falsch decodiert (rote Hinterlegung):

\[{\rm Pr}(\underline{v} \ne \underline{u}) \hspace{-0.1cm} = \hspace{-0.1cm} \sum_{f=2 \atop f \hspace{0.1cm}{\rm gerade} }^{n} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} = 1 - {\rm Pr}(\underline{v} = \underline{u}) - {\rm Pr}(s=1)\approx 0.1\,\%\hspace{0.05cm}.\]

Wir verweisen hier auf das interaktive Applet Binomial- und Poissonverteilung. Die hier gewonnenen Ergebnisse werden auch in der Aufgabe A1.5 nochmals diskutiert.

$\text{Beispiel 2:}$ Eine Fehlerkorrektur des Single Parity–check Codes ist beim BSC–Modell nicht möglich im Unterschied zum BEC–Kanal (Binary Erasure Channel).

Bei diesem werden Bitfehler ausgeschlossen. Ist nur ein Bit ausgelöscht $($englisch: Erasure, $\rm E)$, so ist aufgrund der Tatsache „die Anzahl der Einsen im Codewort ist gerade” auch eine Fehlerkorrektur möglich, zum Beispiel für den $\text{SPC (5, 4, 2)}$:

\[\underline{y} = (1, 0, {\rm E}, 1, 1) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (1, 0, 1, 1, 1) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (1, 0, 1, 1) = \underline{u}\hspace{0.05cm},\] \[\underline{y}=(0, 1, 1, {\rm E}, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (0, 1, 1, 0, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (0, 1, 1, 0) = \underline{u}\hspace{0.05cm},\] \[\underline{y} = (0, 1, 0, 1, {\rm E}) \hspace{0.2cm}\Rightarrow\hspace{0.2cm}\underline{z} = (0, 1, 0, 1, 0) \hspace{0.2cm}\Rightarrow\hspace{0.2cm} \underline{v} = (0, 1, 0, 1) = \underline{u}\hspace{0.05cm}.\]

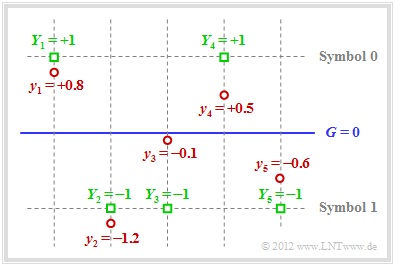
$\text{Beispiel 3:}$ Auch beim AWGN–Kanal ist Fehlerkorrektur möglich, wenn man Soft Decision anwendet. Für das Folgende gehen wir von bipolarer Signalisierung aus:

Zur Verdeutlichung von „Soft Decision” bei AWGN

$x=0$ ⇒ $\tilde{x}= +1$, sowie
$x=1$ ⇒ $\tilde{x}= -1$.

Die Grafik verdeutlicht den hier dargelegten Sachverhalt:

Beispielsweise lautet der Empfangsvektor (rote Punkte):

\[\underline{y} = (+0.8, -1.2, -0.1, +0.5, -0.6) \hspace{0.05cm}.\]

Bei harter Entscheidung (Schwelle $G = 0$, nur die Vorzeichen werden ausgewertet) würde man zu folgendem binären Ergebnis kommen $($grüne Quadrate $Y_i = y_i/ \vert y_i \vert)$:

\[\underline{Y} = (+1, -1, -1, +1, -1) \hspace{0.05cm}.\]

In Symbolschreibweise ergibt sich daraus $(0, 1, 1, 0, 1)$, was kein gültiges Codewort des $\text{SPC (5, 4, 2)}$ ist ⇒ Syndrom $s = 1$. Also müssen ein, drei oder fünf Bit verfälscht worden sein.

Die Wahrscheinlichkeit für drei oder fünf Bitfehler ist allerdings um Größenordnungen kleiner als diejenige für einen einzigen Fehler. Die Annahme „ein Bitfehler” ist deshalb nicht abwegig.

Da der Empfangswert $y_3$ sehr nahe an der Schwelle $G = 0$ liegt, geht man davon aus, dass genau dieses Bit verfälscht wurde.

Damit fällt bei Soft Decision die Entscheidung für $\underline{z} = (0, 1, 0, 0, 1)$ ⇒ $\underline{v} = (0, 1, 0, 0)$.
Die Blockfehlerwahrscheinlichkeit ${\rm Pr}(\underline{v} \ne \underline{u})$ ist so am geringsten.

Wiederholungscodes

$\text{Definition:}$ Ein $\text{Wiederholungscode}$ (englisch: Repetition Code, $\rm RC)$ ist ein linearer binärer $(n, \, k)$–Blockcode der Form

\[\mathcal{C} = \big \{ \underline{x} \in {\rm GF}(2^n)\text{:} \ \ x_i = x_j \hspace{0.15cm}{\rm f\ddot{u}r \hspace{0.15cm}alle\hspace{0.25cm} } i, j = 1, \hspace{0.05cm} \text{...} \hspace{0.05cm}, n \big \}.\]

Der Codeparameter $n$ bezeichnet die Codelänge. Unabhängig von $n$ gilt stets $k = 1$.
Entsprechend existieren nur die zwei Codeworte $(0, 0, \hspace{0.05cm} \text{...} \hspace{0.05cm} , 0)$ und $(1, 1, \hspace{0.05cm}\text{...}\hspace{0.05cm} , 1)$, die sich in $n$ Binärstellen unterscheiden.
Daraus folgt für die minimale Distanz $d_{\rm min} = n$.

Verschiedene Wiederholungscodes (Repetition Codes)

Die Grafik zeigt Wiederholungscodes für

$n=3$,
$n=4$,
$n=5$.

Ein solcher Wiederholungscode weist folgende Eigenschaften auf:

Dieser $(n, \, 1, \, n)$–Blockcode besitzt die sehr kleine Coderate $R = 1/n$, ist also nur für die Übertragung bzw. Speicherung kleiner Dateien geeignet.
Andererseits ist der Wiederholungscode sehr robust.
Insbesondere beim BEC–Kanal (Binary Erasure Channel) genügt ein einziges richtig übertragenes Bit an beliebiger Position (alle anderen Bit können ausgelöscht sein), um das Informationswort richtig zu decodieren.

$\text{Beispiel 4: Decodierung und Fehlerwahrscheinlichkeiten beim BSC–Kanal}$

Es gelte der BSC–Kanal mit $\varepsilon = 10\%$. Die Decodierung basiere auf dem Majoritätsprinzip.

Bei ungeradem $n$ können $e=n-1$ Bitfehler erkannt und $t=(n-1)/2$ Bitfehler korrigiert werden. Damit ergibt sich für die Wahrscheinlichkeit der korrekten Decodierung der Informationsbits $u$:

\[{\rm Pr}(v = u) = \sum_{f=0 }^{(n-1)/2} {n \choose f} \cdot \varepsilon^{f} \cdot (1 - \varepsilon)^{n-f} \hspace{0.05cm}.\]

Die nachfolgenden Zahlenwerte gelten für $n = 5$. Das heißt: Es sind $t = 2$ Bitfehler korrigierbar:

\[{\rm Pr}(v = u) = (1 - \varepsilon)^5 + 5 \cdot \varepsilon \cdot (1 - \varepsilon)^4 + 10 \cdot \varepsilon^2 \cdot (1 - \varepsilon)^3 \approx 99.15\,\%\]

\[\Rightarrow\hspace{0.3cm}{\rm Pr}(v \ne u) = 1- {\rm Pr}(v = u) \approx 0.85\,\%\hspace{0.05cm}.\]

Bei geradem $n$ können dagegen nur $t=n/2-1$ Fehler korrigiert werden. Erhöht man $n$ von $5$ auf $6$, so sind weiterhin auch nur zwei Bitfehler innerhalb eines Codewortes korrigierbar. Einen dritten Bitfehler kann man zwar nicht korrigieren, aber zumindest erkennen:

\[{\rm Pr}({\rm nicht\hspace{0.15cm} korrigierbarer\hspace{0.15cm} Fehler}) = {6 \choose 3} \cdot \varepsilon^{3} \cdot (1 - \varepsilon)^{3}= 20 \cdot 0.1^{3} \cdot 0.9^{3}\approx 1.46\,\%\hspace{0.05cm}. \]

Ein (unerkannter) Decodierfehler $(v \ne u)$ ergibt sich erst, wenn innerhalb des 6 Bit–Wortes vier oder mehr Bit verfälscht wurden. Als Näherung unter der Annahme, dass fünf oder sechs Bitfehler sehr viel unwahrscheinlicher sind als vier, gilt:

\[{\rm Pr}(v \ne u) \approx {6 \choose 4} \cdot \varepsilon^{4} \cdot (1 - \varepsilon)^{2}= 0.122\,\%\hspace{0.05cm}.\]

Interessant ist, dass beim $\text{RC(6, 1, 6)}$ die Wahrscheinlichkeit ${\rm Pr}(v = u)$ für eine mögliche und richtige Decodierung mit $98.42\%$ kleiner ist als beim $\text{RC (5, 1, 5)}$. Für letzteren gilt:

$${\rm Pr}(v = u) = 1- 0.00122 \approx 99.88\%.$$

$\text{Beispiel 5: Leistungsfähigkeit des Wiederholungscodes beim AWGN–Kanal}$

Wir betrachten nun den AWGN–Kanal. Bei uncodierter Übertragung $($oder dem Wiederholungscode mit $n=1)$ ist der Empfangswert $y = \tilde{x}+\eta$, wobei $\tilde{x} \in \{+1, -1\}$ das Informationsbit bei bipolarer Signalisierung bezeichnet und $\eta$ den Rauschterm. Um Verwechslungen mit dem Codeparameter $n$ zu vermeiden, haben wir das Rauschen umbenannt: $n → \eta$.

Für die Fehlerwahrscheinlichkeit gilt mit dem komplementären Gaußschen Fehlerintegral ${\rm Q}(x)$

\[{\rm Pr}(v \ne u) = {\rm Q}(\sqrt{\rho}) \hspace{0.05cm},\]

wobei folgende physikalische Größen zu verwenden sind:

das Signal–zu–Rauschleistungsverhältnis $\rho= 1/\sigma^2 = 2 \cdot E_{\rm S}/N_0$,

die Energie $E_{\rm S}$ pro Codesymbol ⇒ „Symbolenergie”,

die normierte Streuung $\sigma$ des Rauschens, gültig für das bipolare Informationsbit $\tilde{x} \in \{+1, -1\}$, und

die konstante (einseitige) Rauschleistungsdichte $N_0$ des AWGN–Rauschens.

Bei einem $(n, 1, n)$–Wiederholungscode ergibt sich dagegen für den Eingangswert des Maximum–Likelihood–Decoders $y \hspace{0.04cm}' = \tilde{x} \hspace{0.04cm}'+\eta \hspace{0.04cm}'$ mit folgenden Eigenschaften:

Fehlerwahrscheinlichkeit des Wiederholungscodes beim AWGN–Kanal

\[\tilde{x} \hspace{0.04cm}' =\sum_{i=1 }^{n} \tilde{x}_i \in \{ +n, -n \}\hspace{0.2cm} \Rightarrow\hspace{0.2cm} n{\rm -fache \hspace{0.15cm}Amplitude}\]

\[\hspace{4.8cm} \Rightarrow\hspace{0.2cm}n^2{\rm -fache \hspace{0.15cm}Leistung}\hspace{0.05cm},\]

\[\eta\hspace{0.04cm}' = \sum_{i=1 }^{n} \eta_i\hspace{0.2cm} \Rightarrow\hspace{0.2cm} n{\rm -fache \hspace{0.15cm}Varianz:\hspace{0.15cm} } \sigma^2 \rightarrow n \cdot \sigma^2\hspace{0.05cm},\]

\[\rho\hspace{0.04cm}' = \frac{n^2}{n \cdot \sigma^2} = n \cdot \rho \hspace{0.2cm} \Rightarrow\hspace{0.2cm}{\rm Pr}(v \ne u) = {\rm Q}(\sqrt{n \cdot \frac{2E_{\rm S} }{N_0} } )\hspace{0.05cm}.\]

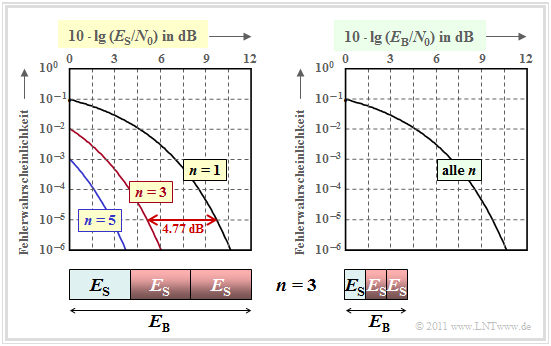
Die Fehlerwahrscheinlichkeit in doppelt logarithmischer Darstellung zeigt die linke Grafik. Als Abszisse ist $10 \cdot \lg \, (E_{\rm S}/N_0)$ aufgetragen. Die Energie pro Bit $(E_{\rm B})$ ist $n$ mal größer als die Symbolenergie $E_{\rm S}$, wie im Schaubild für $n=3$ verdeutlicht.
Diese Kurvenschar kann wie folgt interpretiert werden:

Trägt man die Fehlerwahrscheinlichkeit über der Abszisse $10 \cdot \lg \, (E_{\rm S}/N_0)$ auf, so ergibt sich durch $n$–fache Wiederholung gegenüber uncodierter Übertragung $(n=1)$ eine signifikante Verbesserung.

Die Kurve für den Wiederholungsfaktor $n$ erhält man durch Linksverschiebung um $10 \cdot \lg \, n$ (in dB) gegenüber der Vergleichskurve. Der Gewinn beträgt $4.77 \ {\rm dB} \ (n = 3)$ bzw. $\approx 5 \ {\rm dB} \ (n = 5)$.

Allerdings ist ein Vergleich bei konstantem $E_{\rm S}$ nicht fair, da man mit dem Repetition Code $\text{RC (5, 1, 5)}$ für die Übertragung eines Informationsbits eine um den Faktor $n$ größere Energie aufwendet als bei uncodierter Übertragung: $E_{\rm B} = E_{\rm S}/{R} = n \cdot E_{\rm S}\hspace{0.05cm}.$

Aus der rechten Grafik erkennt man, dass alle Kurven genau übereinander liegen, wenn auf der Abszisse $10 \cdot \lg \, (E_{\rm B}/N_0)$ aufgetragen wird.

$\text{Fazit bezüglich Wiederholungscodes beim AWGN–Kanal:}$

Die Fehlerwahrscheinlichkeit ist bei fairem Vergleich unabhängig vom Wiederholungsfaktor $n$: ${\rm Pr}(v \ne u) = {\rm Q}\left (\sqrt{2E_{\rm B} /{N_0} } \right ) \hspace{0.05cm}.$

Beim AWGN–Kanal ist durch einen Wiederholungscode kein Codiergewinn zu erzielen.

Hamming–Codes

Richard Wesley Hamming hat 1962 eine Klasse binärer Blockcodes angegeben, die sich durch die Anzahl $m = 2, 3, \text{...} $ der zugesetzten Parity Bits unterscheiden. Für diese Codeklasse gilt:

Die Codelänge ergibt sich stets zu $n = 2^m -1$. Möglich sind demzufolge beim Hamming–Code auch nur die Längen $n = 3$, $n = 7$, $n = 15$, $n = 31$, $n = 63$, $n = 127$, $n = 255$, usw.

Ein Informationswort besteht aus $k = n-m$ Bit. Die Coderate ist somit gleich

\[R = \frac{k}{n} = \frac{2^m - 1 - m}{2^m - 1} \in \{1/3, \hspace{0.1cm}4/7,\hspace{0.1cm}11/15,\hspace{0.1cm}26/31,\hspace{0.1cm}57/63, \hspace{0.1cm}120/127,\hspace{0.1cm}247/255, \hspace{0.05cm} \text{...} \hspace{0.05cm} \}\hspace{0.05cm}.\]

Alle Hamming–Codes weisen die minimale Distanz $d_{\rm min} = 3$ auf. Bei größerer Codelänge $n$ erreicht man $d_{\rm min} = 3$ schon mit weniger Redundanz, also bei größerer Coderate $R$.

Aus der Angabe $d_{\rm min} = 3$ folgt weiter, dass hier $e = d_{\rm min} -1 =2$ Fehler erkannt werden können und man $t = (d_{\rm min} -1)/2 = 1$ Fehler korrigieren kann.

Der Hamming–Code $\text{HC (3, 1, 3)}$ ist identisch mit dem Wiederholungscode $\text{RP (3, 1, 3)}$ und lautet:

\[\mathcal{C} = \big \{ (0, 0, 0) \hspace{0.05cm}, (1, 1, 1) \big \}\hspace{0.05cm}. \]

Bei systematischer Codierung sind die ersten $k$ Stellen eines jeden Hamming–Codewortes $\underline{x}$ identisch mit dem Informationswort $\underline{u}$. Anschließend folgen dann die $m = n-k$ Paritätsbit:

\[\underline{x} = ( x_1, x_2,\hspace{0.05cm}\text{...} \hspace{0.05cm}, x_n) = ( u_1, u_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_k, p_1, p_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, p_{n-k}) \hspace{0.05cm}.\]

Verdeutlichung des $\text{(7, 4, 3)}$–Hamming–Codes

$\text{Beispiel 6: Paritätsgleichungen des (7, 4, 3)-Hamming-Codes}$
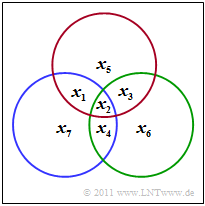
Der $\text{(7, 4, 3)}$–Hamming–Code wird durch das dargestellte Schaubild verdeutlicht. Daraus kann man die drei Bedingungen ableiten:

\[x_1 \oplus x_2 \oplus x_3 \oplus x_5 \hspace{-0.1cm} = \hspace{-0.1cm} 0 \hspace{0.05cm},\]

\[x_2 \oplus x_3 \oplus x_4 \oplus x_6 \hspace{-0.1cm} = \hspace{-0.1cm} 0 \hspace{0.05cm},\]

\[x_1 \oplus x_2 \oplus x_4 \oplus x_7 \hspace{-0.1cm} = \hspace{-0.1cm} 0 \hspace{0.05cm}. \]

Im Schaubild kennzeichnet der rote Kreis die erste Prüfgleichung, der grüne die zweite und der blaue die letzte.
In jedem Kreis muss die Anzahl der Einsen geradzahlig sein.

Zuordnung $\underline{u} → \underline{x}$ des systematischen $\text{(7, 4, 3)}$–Hamming–Codes

Bei systematischer Codierung des $\text{(7, 4, 3)}$–Hamming–Codes

\[x_1 = u_1 ,\hspace{0.2cm} x_2 = u_2 ,\hspace{0.2cm} x_3 = u_3 ,\hspace{0.2cm} x_4 = u_4 ,\hspace{0.2cm} x_5 = p_1 ,\hspace{0.2cm} x_6 = p_2 ,\hspace{0.2cm} x_7 = p_3 \]

lauten die Bestimmungsgleichungen der drei Prüfbit, wie aus dem Schaubild hervorgeht:

\[p_1 =u_1 \oplus u_2 \oplus u_3 \hspace{0.05cm},\]

\[p_2 = u_2 \oplus u_3 \oplus u_4 \hspace{0.05cm},\]

\[p_3 = u_1 \oplus u_2 \oplus u_4 \hspace{0.05cm}.\]

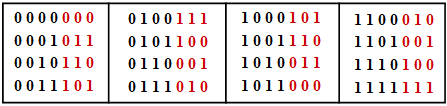
Die Tabelle zeigt die $2^k = 16$ zulässigen Codeworte des systematischen $\text{(7, 4, 3)}$–Codes:

$$\underline{x} = ( x_1, x_2, x_3, x_4, x_5, x_6, x_7) = ( u_1, u_2, u_3, u_4, p_1, p_2, p_3).$$

Das Informationswort $\underline{u} =( u_1, u_2, u_3, u_4)$ ist schwarz dargestellt und die Prüfbits $p_1$, $p_2$ und $p_3$ rot.
Man erkennt anhand dieser Tabelle, dass sich jeweils zwei der $16$ möglichen Codeworte in mindestens $d_{\rm min} = 3$ Binärwerten unterscheiden.

Später wird die Decodierung linearer Blockcodes noch ausführlich behandelt. Das folgende Beispiel soll die Decodierung des Hamming–Codes eher intuitiv erklären.

$\text{Beispiel 7: Paritätsgleichungen des (7, 4, 3)-Hamming-Codes}$

Wir gehen weiter vom systematischen $\text{(7, 4, 3)}$–Code aus und betrachten das Empfangswort $\underline{y} = ( y_1, y_2, y_3, y_4, y_5, y_6, y_7)$. Zur Decodierung bilden wir die drei Paritätsgleichungen

\[ y_1 \oplus y_2 \oplus y_3 \oplus y_5 \hspace{-0.1cm}= \hspace{-0.1cm} 0 \hspace{0.05cm},\hspace{0.5cm}{\rm (I)} \]

\[y_2 \oplus y_3 \oplus y_4 \oplus y_6 \hspace{-0.1cm}= \hspace{-0.1cm}0 \hspace{0.05cm},\hspace{0.5cm}{\rm (II)} \]

\[y_1 \oplus y_2 \oplus y_4 \oplus y_7 \hspace{-0.1cm}= \hspace{-0.1cm} 0\hspace{0.05cm}. \hspace{0.5cm}{\rm (III)}\]

Unter der Voraussetzung, dass in jedem Codewort höchstens ein Bit verfälscht wird, gelten dann die folgenden Aussagen. Im Folgenden bezeichnet $\underline{v}$ das Decodierergebnis; dieses sollte stets mit $\underline{u} = (1, 0, 1, 0)$ übereinstimmen:

Das Empfangswort $\underline{y} = (1, 0, 1, 0, 0, 1, 1)$ erfüllt alle drei Paritätsgleichungen. Das heißt, dass kein einziger Übertragungsfehler aufgetreten ist ⇒ $\underline{y} = \underline{x}$ ⇒ $\underline{v} = \underline{u} = (1, 0, 1, 0)$.

Werden zwei der drei Paritätsgleichungen erfüllt wie zum Beispiel für das empfangene Wort $\underline{y} =(1, 0, 1, 0, 0, 1, 0)$, so wurde ein Paritätsbit verfälscht und es gilt auch hier $\underline{v} = \underline{u} = (1, 0, 1, 0)$.

Mit $\underline{y} = (1, 0, 1, 1, 0, 1, 1)$ wird nur die Gleichung $\rm (I)$ erfüllt und die beiden anderen nicht. Somit kann man die Verfälschung des vierten Binärsymbols korrigieren, und es gilt auch hier $\underline{v} = \underline{u} = (1, 0, 1, 0)$.

Ein Übertragungsfehler des zweiten Bits ⇒ $\underline{y} = (1, 1, 1, 0, 0, 1, 1)$ führt dazu, dass alle drei Paritätsgleichungen nicht erfüllt werden. Auch dieser Fehler lässt sich eindeutig korrigieren da nur $u_2$ in allen Gleichungen vorkommt.

Aufgaben zum Kapitel

Aufgabe 1.5: SPC (5, 4) und BEC–Modell

Aufgabe 1.5Z: SPC (5, 4) vs. RC (5, 1)

Aufgabe 1.6: Zum (7, 4)–Hamming–Code

Examples of Binary Block Codes

Contents

Single Parity–check Codes

Wiederholungscodes

Hamming–Codes

Aufgaben zum Kapitel