Exercise 1.5Z: Sinc-shaped Impulse Response

• Return to book

$\rm sinc$–shaped impulse response

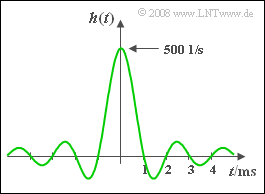
The impulse response of a linear time-invariant (and non-causal) system was determined as follows (see graph):

$$h(t) = 500\hspace{0.1cm}{ {\rm s}}^{-1}\cdot{\rm sinc}\big[{t}/({ 1\hspace{0.1cm}{\rm ms}})\big] .$$

The output signals  $y(t)$ should be computed if various cosine oscillations of different frequency  $f_0$  are applied to the input:

$$x(t) = 4\hspace{0.05cm}{\rm V}\cdot {\rm cos}(2\pi \cdot f_0 \cdot t ) .$$

Please note:

• The exercise belongs to the chapter  Some Low-Pass Functions in Systems Theory.
• The solution can be found in the time domain or in the frequency domain. In the sample solution you will find both approaches.
• The following definite integral is given:

$$\int_{ 0 }^{ \infty } \frac{\sin(u) \cdot \cos(a \cdot u)}{u} \hspace{0.15cm}{\rm d}u = \left\{ \begin{array}{c} \pi/2 \\ \pi/4 \\ 0 \\ \end{array} \right.\quad \quad \begin{array}{c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c}{ |a| < 1,} \\{ |a| = 1,} \\ { |a| > 1.} \\ \end{array}$$

Questions

1

Compute the frequency response  $H(f)$  of the LTI system. What is the equivalent bandwidth and the direct signal (DC) transmission factor?

$\Delta f \ =\ $ $\ \rm kHz$

$H(f = 0) \ =\ $

2

What is the signal value of the output signal  $y(t)$  at time  $t = 0$  if the input is cosine-shaped and of frequency  $\underline{f_0 = 1\ \rm kHz}$?

$y(t = 0) \ = \ $ $\ \rm V$

3

What is the signal value of the output signal  $y(t)$  at time  $t = 0$  if the input is cosine-shaped and of frequency  $\underline{f_0 = 0.1\ \rm kHz}$?

$y(t = 0) \ =\ $ $\ \rm V$

4

What is the signal value of the output signal  $y(t)$  at timee  $t = 0$  if the input is cosine-shaped and of frequency  $\underline{f_0 = 0.5\ \rm kHz}$?

$y(t = 0) \ = \ $ $\ \rm V$

Solution

Solution

(1)  A comparison with the equations on the page  [[Linear_and_Time_Invariant_Systems/Some_Low-Pass_Functions_in_Systems_Theory#Ideal_low-pass_filter_–_Rectangular-in-frequency |Ideal low-pass filter]] or applying the  inverse Fourier transformation  shows that  $H(f)$  is an ideal low-pass filter:

$$H(f) = \left\{ \begin{array}{c} \hspace{0.25cm}K \\ K/2 \\ 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < \Delta f/2,} \\ {\left| \hspace{0.005cm}f\hspace{0.05cm} \right| = \Delta f/2,} \\ {\left|\hspace{0.005cm} f \hspace{0.05cm} \right| > \Delta f/2.} \\ \end{array}$$

• The equidistant zero-crossings of the impulse response occur at an interval of  $Δt = 1 \ \rm ms$ .
• From this it follows that the equivalent bandwidth is  $Δf \rm \underline{ = 1 \ \rm kHz}$. 
• If  $K = 1$ was true, then  $h(0) = Δf = 1000 \cdot \rm 1/s$  should hold.
• Because of the given  $h(0) = 500 \cdot{\rm 1/s} = Δf/2$  the direct signal (DC) transmission factor thus is  $K = H(f = 0) \; \rm \underline{= 0.5}$.

(2)  This problem is most easily solved in the spectral domain.

• For the output spectrum the following holds:   $Y(f) = X(f)\cdot H(f) .$
• $X(f)$  consists of two Dirac functions at  $± f_0$ each with weight  $A_x/2 =2 \hspace{0.08cm}\rm V$.
• For  $f = f_0 = 1 \ {\rm kHz} > Δf/2$ , however  $H(f) = 0$ holds, such that  $Y(f) = 0$  and hence also   $y(t) = 0$    ⇒   $\underline{y(t = 0) = 0}$.

The solution in the time domain is based on convolution:

$$y(t) = x (t) * h (t) = \int_{ - \infty }^{ + \infty } {h ( \tau )} \cdot x ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$

• At time  $t = 0$  the following is obtained considering the symmetry of the cosine function:

$$y(t = 0 ) = \frac{A_x \cdot \Delta f}{2} \cdot \int_{ - \infty }^{ + \infty } {\rm si} ( \pi \cdot \Delta f \cdot \tau ) \cdot {\rm cos}(2\pi \cdot f_0 \cdot \tau ) \hspace{0.1cm}{\rm d}\tau.$$

• With the substitution  $u = π · Δf · τ$ , this can also be formulated as follows:

$$y(t = 0 ) = \frac{A_x }{\pi} \cdot \int_{ 0 }^{ \infty } \frac{\sin(u) \cdot \cos(a \cdot u)}{u} \hspace{0.15cm}{\rm d}u .$$

• Here, the constant is  $a = 2f_0/Δf = 2$. With this value, the given integral yields zero:   $y(t = 0 ) = {A_y } = 0.$

(3)  The frequency response has the value  $K = 0.5$ at  $f = f_0 = 100 \ \rm Hz$  according to the calculations for subtask  (1) . Therefore,

$$A_y = A_x/2 = 2\ \rm V$$ is obtained.

• The same result is obtained by convolution according to the above equation.
• For  $a = 2f_0/Δf = 0.2$  the integral is equal to  $π/2$  and one obtains

$$y(t = 0 ) = {A_y } = \frac{A_x}{\pi} \cdot \frac{\pi}{2} = \frac{A_x}{2} \hspace{0.15cm}\underline{= 2\,{\rm V}}.$$

(4)  The transition from the band-pass to the band-stop is exactly at  $f = 0.5 \ \rm kHz$  and for this singular location the following holds:

$$H(f = f_0) = K/2.$$

• Thus, the amplitude of the output signal is only half as large as calculated in subtask  (3) , namely  $A_y \; \underline{= 1 \, \rm V}$.
• The same result is obtained with $a = 2f_0/Δf = 1$  by convolution.