Exercise 1.8: Variable Edge Steepness
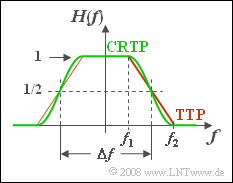
Two low-pass filters with variable edge steepnesses are compared with each other. For frequencies $|f| ≤ f_1$ , $H(f) = 1$ holds in both cases. In contrast, all frequencies $|f| ≥ f_2$ are suppressed entirely.
In the range $f_1 ≤ |f| ≤ f_2$ the frequency responses are defined by the following equations:
- Trapezoidal low-pass filter (TTP):
- $$H(f) = \frac{f_2 - |f|}{f_2 - f_1} ,$$
- Raised-cosine low-pass filter (CRTP):
- $$H(f) = \cos^2 \left(\frac{|f|- f_1}{f_2 - f_1} \cdot\frac{\pi}{2} \right).$$
Alternative system parameters for both low-pass filters are
- the equivalent bandwidth $Δf$ defined by the equal-area rectangle, and also
- the roll-off factor (in frequency domain):
- $$r=\frac{f_2 - f_1}{f_2 + f_1} .$$
Throughout the task, $Δf = 10 \ \rm kHz$ and $r = 0.2$ hold true.
The impulse responses are with equivalent impulse duration $Δt = 1/Δf = 0.1 \ \rm ms$:
- $$h_{\rm TTP}(t) = \frac{1}{\Delta t} \cdot {\rm si}(\pi \cdot \frac{t}{\Delta t} )\cdot {\rm si}(\pi \cdot r \cdot \frac{t}{\Delta t} ),$$
- $$h_{\rm CRTP}(t) = \frac{1}{\Delta t} \cdot {\rm si}(\pi \cdot \frac{t}{\Delta t} )\cdot \frac {\cos(\pi \cdot r \cdot t / \Delta t )}{1 - (2 \cdot r \cdot t/\Delta t )^2}.$$
Please note:
- The exercise belongs to the chapter Some Low-Pass Functions in Systems Theory.
- In particular, reference is made to the pages Trapezoidal low-pass filter and Raised-cosine low-pass filter.
- You can check your results with the interactive applet Frequency response and impulse respond .
Questions
Solution
- For both low-pass filters, the integral over $H(f)$ is equal to $f_1 + f_2$.
- Thus, due to $H(f = 0 = 1)$ Approach 2 is correct: $\Delta f = f_1 + f_2.$
(2) Setzt man die unter (1) gefundene Beziehung in die Definitionsgleichung des Rolloff–Faktors ein, so erhält man
- $${f_2 - f_1} = r \cdot \Delta f = {2\,\rm kHz}, \hspace{0.5cm} {f_2 + f_1} = {10\,\rm kHz}.$$
- Durch Addition bzw. Subtraktion beider Gleichungen ergeben sich die so genannten "Eckfrequenzen" zu
- $$f_1 \underline{= 4 \ \rm kHz},$$
- $$f_2 \underline{= 6 \ \rm kHz}.$$
(3) Richtig sind die Lösungsvorschläge 1 und 4:
- Die erste $\rm si$–Funktion von $h_{\rm TTP}(t)$ führt zu Nullstellen im Abstand $\Delta t$ (siehe auch Gleichung auf der Angabenseite).
- Die zweite $\rm si$–Funktion bewirkt Nullstellen bei Vielfachen von $5 · \Delta t$.
- Da diese exakt mit den Nullstellen der ersten $\rm si$–Funktion zusammenfallen, gibt es keine zusätzlichen Nullstellen.
- Der Sonderfall $r = 0$ entspricht dem idealen rechteckförmigen Tiefpass mit $\rm si$–förmiger Impulsantwort. Diese klingt extrem langsam ab.
- Die $\rm si^2$–förmige Impulsantwort des Dreiecktiefpasses $($Sonderfall für $r = 1)$ fällt asymptotisch mit $1/t^2$, also schneller als mit $r = 0.2$.
(4) Richtig sind hier die Vorschläge 1, 2 und 4:
- Die Impulsantwort $h_{\rm CRTP}(t)$ des Cosinus-Rolloff-Tiefpasses hat aufgrund der si–Funktion ebenfalls Nullstellen im Abstand $\Delta t$.
- Die Cosinusfunktion hat Nullstellen zu folgenden Zeitpunkten:
- $${\cos(\pi \cdot r \cdot {t}/{ \Delta t} )} = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}r \cdot {t}/{ \Delta t} = \pm 0.5, \pm 1.5, \pm 2.5, \text{...} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {t}/{ \Delta t} = \pm 2.5, \pm 7.5, \pm 12.5, ... $$
- $$\Rightarrow \hspace{0.3cm} {t}/{ \Delta t} = \pm 2.5, \pm 7.5, \pm 12.5, \text{...}. $$
- Die Nullstelle des Zählers bei $t / \Delta t = 2.5$ wird allerdings durch den ebenfalls verschwindenden Nenner zunichte gemacht.
- Die weiteren Nullstellen bei $7.5, 12.5,\text{...} $ bleiben dagegen bestehen.
- Auch hier führt $r = 0$ zum Rechtecktiefpass und damit zur $\rm si$–förmigen Impulsantwort.
- Dagegen klingt die Impulsantwort des Cosinus–Quadrat–Tiefpasses $($Sonderfall für $r = 1)$ extrem schnell ab.
- Dieser wird in der Aufgabe 1.8Z eingehend untersucht.