Exercise 2.9: Symmetrical Distortions

Transmitter and receiver spectrum in the equivalent low-pass region

The source signal made up of two components

$$q(t) = A_1 \cdot \cos(2 \pi f_1 t ) + A_2 \cdot \cos(2 \pi f_2 t )$$

is amplitude modulated and transmitted through a linearly distorting transmission channel. The carrier frequency is $f_{\rm T}$ and the added DC component $A_{\rm T}$. Thus, a Double-sideband amplitude moduluation $\rm (DSB–AM)$ with carrier is present.

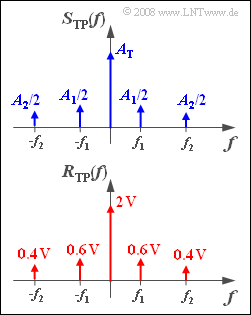
The upper graph shows the spectrum $S_{\rm TP}(f)$ of the equivalent low-pass signal in schematic form. This means that the lengths of the Dirac lines drawn do not correspond to the actual values of $A_{\rm T}$, $A_1/2$ and $A_2/2$ .

The spectral function $R(f)$ of the received signal was measured. In the lower graph we can observe the equivalent low-pass spectrum $R_{\rm TP}(f)$ calculated from this.

The channel frequency response is characterised with sufficient accuracy with a few auxiliary values:

$$ H_{\rm K}(f = f_{\rm T}) = 0.5,$$

$$H_{\rm K}(f = f_{\rm T} \pm f_1) = 0.4,$$

$$ H_{\rm K}(f = f_{\rm T} \pm f_2) = 0.2 \hspace{0.05cm}.$$

Hints:

This exercise belongs to the chapternbsp; Envelope Demodulation.
Particular reference is made to the page Description using the equivalent low-pass signal.

Questions

$A_{\rm T} \ = \hspace{0.17cm} $

$\ \rm V$

$A_1 \ = \ $

$\ \rm V$

$A_2 \ = \ $

$\ \rm V$

	No distortion.
	Linear distortions.
	Nonlinear distortions.

	$r_{\rm TP}(t)$ is always real,
	$r_{\rm TP}(t)$ is always greater than or equal to zero,
	the phase function $ϕ(t)$ can take on the values $0^\circ$ and $180^\circ$ .

	No distortion.
	Linear distortions.
	Nonlinear distortions.

Solution

(1) On the basis of the graphs on the exercise page, the following statements can be made:

$${A_{\rm T}} \cdot 0.5 = 2 \,{\rm V}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}A_{\rm T} \hspace{0.15cm}\underline {= 4 \,{\rm V}},$$

$${A_{\rm 1}}/{2} \cdot 0.4 = 0.6\,{\rm V}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}A_{\rm 1} \hspace{0.15cm}\underline {= 3 \,{\rm V}},$$

$${A_{\rm 2}}/{2} \cdot 0.2 = 0.4\,{\rm V}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}A_{\rm 2} \hspace{0.15cm}\underline {= 4 \,{\rm V}}\hspace{0.05cm}.$$

(2) Answer 3 is correct:

The resulting modulation depth is $m = (A_1 + A_2)/A_T = 1.75$.
This leads to strong nonlinear distortion when using an envelope demodulator.
A distortion factor cannot be specified because the source signal contains two frequency components.

(3) Answers 1 and 2 are correct:

The Fourier retransform of $R_{\rm TP}(f)$ gives us the result:

$$ r_{\rm TP}(t) = 2 \,{\rm V} + 1.2 \,{\rm V} \cdot \cos(2 \pi f_1 t ) + 0.8 \,{\rm V} \cdot \cos(2 \pi f_2 t )\hspace{0.05cm}.$$

This function is always real and non-negative.
Thus, $ϕ(t) = 0$. holds simultaneously, whereas $ϕ(t) = 180^\circ$ is not possible.

(4) A comparison of the two signals

$$q(t) = 3 \,{\rm V} \cdot \cos(2 \pi f_1 t ) + 4 \,{\rm V} \cdot \cos(2 \pi f_2 t ),$$

$$ v(t) = 0.4 \cdot 3 \,{\rm V} \cdot \cos(2 \pi f_1 t ) + 0.2 \cdot 4 \,{\rm V} \cdot \cos(2 \pi f_2 t )$$

shows, that linear distortions now arise – attenuation distortions to be precise ⇒ Answer 2.

Here, the channel $H_{\rm K}(f)$ has the positive effect, that instead of irreversible nonlinear distortions, linear distortions occur that can be eliminated by a downstream filter.
This is due to the fact that the higher attenuation of the source signal $q(t)$ compared to the carrier signal $z(t)$ lowers the modulation depth from n $m = 1.75$ to $m = (0.4 · 3 \ \rm V + 0.2 · 4 \ \rm V)/(0.5 · 4 \ \rm V) = 1$ .