Two-Dimensional Random Variables

1 # OVERVIEW OF THE FOURTH MAIN CHAPTER #
2 Properties and examples
3 Joint PDF
4 Two-dimensional CDF
5 PDF and CDF for statistically independent components
6 PDF and CDF for statistically dependent components
7 Expected values of two-dimensional random variables
8 Correlation coefficient
9 Korrelationsgerade
10 Aufgaben zum Kapitel

# OVERVIEW OF THE FOURTH MAIN CHAPTER #

Now random variables with statistical bindings are treated and illustrated by typical examples. After the general description of two-dimensional random variables, we turn to the autocorrelation function (ACF), the cross correlation function (CCF) and the associated spectral functions (PSD, CPSD) .

Specifically, it covers:

the statistical description of 2D random variables using the (joint) PDF,
the difference between statistical dependence and correlation, ???
the classification features stationarity and ergodicity of stochastic processes,
the definitions of autocorrelation function (ACF) and power spectral density (PSD),
the definitions of cross correlation function and cross power spectral density, and
the numerical determination of all these quantities in the two- and multi-dimensional cases.

For more information on Two-Dimensional Random Variables, as well as tasks, simulations, and programming exercises, see

Chapter 5: Two-dimensional random variables (program "zwd")
Chapter 9: Stochastic Processes (program "sto")

of the practical course "Simulation Methods in Communications Engineering". This (former) LNT course at the TU Munich is based on

the teaching software package LNTsim ⇒ Link refers to the German ZIP–version of the program,
Internship Guide – Part A ⇒ Link refers to the German PDF–version with chapter 5: pages 81-97,
the Internship Guide – Part B ⇒ Link refers to the German PDF–version with chapter 9: pages 207-228.

Properties and examples

As a transition to the correlation functions we now consider two random variables $x$ and $y$, between which statistical bindings(???) exist. Each of the two random variables can be described on its own with the introduced characteristic quantities

corresponding to the second main chapter ⇒ Discrete Random Variables
but the third main chapter ⇒ Continuous Random Variables.

$\text{Definition:}$ To describe the correlations between two variables $x$ and $y$ it is convenient to combine the two components into one two-dimensional random variable $(x, y)$ }.

The individual components can be signals such as the real– and imaginary parts of a phase modulated signal.
But there are a variety of 2D–random variables in other domains as well, as the following example will show

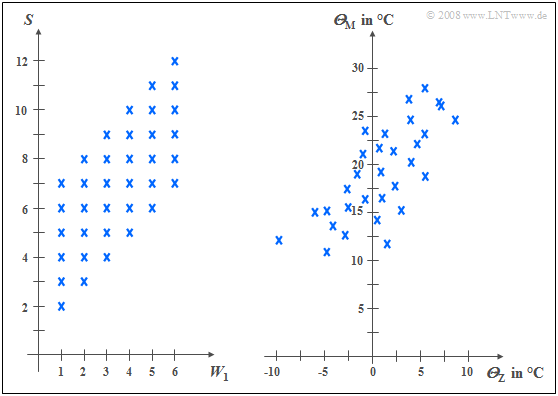
$\text{Example 1:}$ The left diagram is from the random experiment "Throwing two dice". Plotted to the right is the number of the first die $(W_1)$, plotted to the top is the sum $S$ of both dice. The two components here are each discrete random variables between which there are statistical dependencies(???):

If $W_1 = 1$, then $S$ can only take values between $2$ and $7$ and each with equal probability.
In contrast, for $W_1 = 6$ all values between $7$ and $12$ are possible, also with equal probability.

Two examples of statistically dependent random variables

In the right graph, the maximum temperatures of the $31$ days in May 2002 of Munich (to the top) and the Zugspitze (to the right) are contrasted. Both random variables are continuous in value:

although the measurement points are about $\text{100 km}$ apart, and on the Zugspitze, due to the different altitudes $($nearly $3000$ versus $520$ meters$)$ is on average about $20$ degrees colder than in Munich, one recognizes nevertheless a certain statistical dependence between the two random variables ${\it Θ}_{\rm M}$ and ${\it Θ}_{\rm Z}$.
If it is warm in Munich, then pleasant temperatures are also more likely to be expected on the Zugspitze. However, the relationship is not deterministic: The coldest day in May 2002 was a different day in Munich than the coldest day on the Zugspitze.

Joint PDF

We restrict ourselves here mostly to continuous random variables. However, sometimes the peculiarities of two-dimensional discrete random variables are discussed in more detail. Most of the characteristics previously defined for one-dimensional random variables can be easily extended to two-dimensional variables.

$\text{Definition:}$ The probability density function of the two-dimensional random variable at the location $(x_\mu, y_\mu)$ ⇒ joint PDF is an extension of the one-dimensional PDF $(∩$ denotes logical AND operation$)$:

$$f_{xy}(x_\mu, \hspace{0.1cm}y_\mu) = \lim_{\left.{\delta x\rightarrow 0 \atop {\delta y\rightarrow 0} }\right. }\frac{ {\rm Pr}\big [ (x_\mu - {\rm \Delta} x/{\rm 2} \le x \le x_\mu + {\rm \Delta} x/{\rm 2}) \cap (y_\mu - {\rm \Delta} y/{\rm 2} \le y \le y_\mu +{\rm \Delta}y/{\rm 2}) \big] }{ {\rm \delta} \ x\cdot{\rm \Delta} y}.$$

$\rm Note$:

If the 2D–random variable is discrete, the definition must be slightly modified:
For the lower range limits in each case, the "≤" sign must then be replaced by the "<" sign according to the page CDF for discrete random variables

.

Using this (joint) WDF $f_{xy}(x, y)$ statistical dependencies within the two-dimensional random variable $(x, y)$ are also fully captured in contrast to the two one-dimensional density functions ⇒ marginal probability density functions:

$$f_{x}(x) = \int _{-\infty}^{+\infty} f_{xy}(x,y) \,\,{\rm d}y ,$$

$$f_{y}(y) = \int_{-\infty}^{+\infty} f_{xy}(x,y) \,\,{\rm d}x .$$

These two marginal density functions $f_x(x)$ and $f_y(y)$

provide only statistical information about the individual components $x$ and $y$, respectively,
but not about the bindings between them.

Two-dimensional CDF

$\text{Definition:}$ The 2D distribution function like the 2D WDF, is merely a useful extension of the one-dimensional distribution function (CDF):

$$F_{xy}(r_{x},r_{y}) = {\rm Pr}\big [(x \le r_{x}) \cap (y \le r_{y}) \big ] .$$

The following similarities and differences between the 1D CDF and the 2D CDF emerge:

The functional relationship between two-dimensional PDF and two-dimensional VTF is given by integration as in the one-dimensional case, but now in two dimensions. For continuous random variables:

$$F_{xy}(r_{x},r_{y})=\int_{-\infty}^{r_{y}} \int_{-\infty}^{r_{x}} f_{xy}(x,y) \,\,{\rm d}x \,\, {\rm d}y .$$

Inversely, the probability density function can be given from the distribution function by partial differentiation to $r_{x}$ and $r_{y}$ :

$$f_{xy}(x,y)=\frac{{\rm d}^{\rm 2} F_{xy}(r_{x},r_{y})}{{\rm d} r_{x} \,\, {\rm d} r_{y}}\Bigg|_{\left.{r_{x}=x \atop {r_{y}=y}}\right.}.$$

Relative to the distribution function $F_{xy}(r_{x}, r_{y})$ the following limits apply:

$$F_{xy}(-\infty,-\infty) = 0,$$

$$F_{xy}(r_{\rm x},+\infty)=F_{x}(r_{x} ),$$

$$F_{xy}(+\infty,r_{y})=F_{y}(r_{y} ) ,$$

$$F_{xy} (+\infty,+\infty) = 1.$$

In the limiting case $($infinitely large $r_{x}$ and $r_{y})$ Thus, for the 2D VTF, the value $1$. From this, we obtain the normalization condition for the 2D WDF:

$$\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f_{xy}(x,y) \,\,{\rm d}x \,\,{\rm d}y=1 . $$

$\text{Conclusion:}$ Note the significant difference between one-dimensional and two-dimensional random variables:

For one-dimensional random variables, the area under the PDF always yields the value $1$.
For two-dimensional random variables, the PDF volume is always equal $1$.

PDF and CDF for statistically independent components

For statistically independent components $x$ and $y$ the following holds for the joint probability according to the elementary laws of statistics if $x$ and $y$ are continuous in value:

$${\rm Pr} \big[(x_{\rm 1}\le x \le x_{\rm 2}) \cap( y_{\rm 1}\le y\le y_{\rm 2})\big] ={\rm Pr} (x_{\rm 1}\le x \le x_{\rm 2}) \cdot {\rm Pr}(y_{\rm 1}\le y\le y_{\rm 2}) .$$

For this, independent components can also be written:

$${\rm Pr} \big[(x_{\rm 1}\le x \le x_{\rm 2}) \cap(y_{\rm 1}\le y\le y_{\rm 2})\big] =\int _{x_{\rm 1}}^{x_{\rm 2}}f_{x}(x) \,{\rm d}x\cdot \int_{y_{\rm 1}}^{y_{\rm 2}} f_{y}(y) \, {\rm d}y.$$

$\text{Definition:}$ It follows that for statistical independence the following condition must be satisfied with respect to the 2D–probability density function:

$$f_{xy}(x,y)=f_{x}(x) \cdot f_y(y) .$$

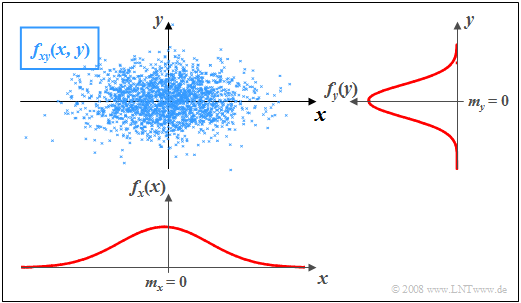
$\text{Example 2:}$ In the graph, the instantaneous values of a two-dimensional random variable are plotted as points in the $(x, y)$–plane.

Ranges with many points, which accordingly appear dark, indicate large values of the 2D–WDF $f_{xy}(x, y)$.
In contrast, the random variable $(x, y)$ has relatively few components in rather bright areas.

Statistically independent components: $f_{xy}(x,y)$, $f_{x}(x)$ and $f_{y}(y)$

The graph can be interpreted as follows:

The marginal probability densities $f_{x}(x)$ and $f_{y}(y)$ already indicate that both $x$ and $y$ are Gaussian and zero mean, and that the random variable $x$ has a larger standard deviation than $y$ .
$f_{x}(x)$ and $f_{y}(y)$ however, do not provide information on whether or not statistical bindings exist for the random variable $(x, y)$ .
However, using the 2D WDF $f_{xy}(x,y)$ one can see that there are no statistical bindings between the two components $x$ and $y$ here.
With statistical independence, any cut through $f_{xy}(x, y)$ parallel to $y$-axis yields a function that is equal in shape to the edge–WDF $f_{y}(y)$. Similarly, all cuts parallel to $x$-axis are equal in shape to $f_{x}(x)$.

This fact is equivalent to saying that in this example $f_{xy}(x, y)$ can be represented as the product of the two marginal probability densities: $f_{xy}(x,y)=f_{x}(x) \cdot f_y(y) .$

PDF and CDF for statistically dependent components

If there are statistical bindings between $x$ and $y$, then different cuts parallel to $x$– and $y$–axis, respectively, yield different, non-shape equivalent functions. In this case, of course, the joint–WDF cannot be described as a product of the two (one-dimensional) marginal probability densities either.

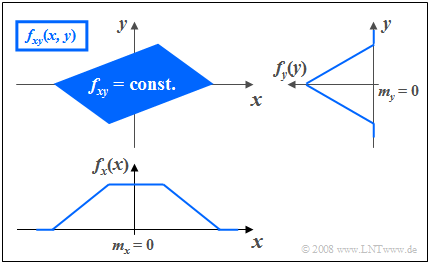
Statistically dependent components: $f_{xy}(x,y)$, $f_{x}(x)$, $f_{y}(y)$

$\text{Example 3:}$ The graph shows the instantaneous values of a two-dimensional random variable in the $(x, y)$–plane, where now, unlike $\text{Example 2}$ there are statistical bindings between $x$ and $y$ .

The 2D–random variable takes all 2D–values with equal probability in the parallelogram drawn in blue.
No values are possible outside the parallelogram.

One recognizes from this representation:

Integration over $f_{xy}(x, y)$ parallel to $x$–axis leads to the triangular marginal density $f_{y}(y)$, integration parallel to $y$–axis to the trapezoidal WDF $f_{x}(x)$.
From the 2D WDF $f_{xy}(x, y)$ it can already be guessed that for each $x$–value on statistical average a different $y$–value is to be expected.
This means that here the components $x$ and $y$ are statistically dependent on each other.

Expected values of two-dimensional random variables

A special case of statistical dependence is correlation.

$\text{Definition:}$ Under correlation one understands a linear dependence between the individual components $x$ and $y$.

Correlated random variables are thus always also statistically dependent.
But not every statistical dependence implies correlation at the same time

.

To quantitatively capture correlation, one uses various expected values of the 2D random variable $(x, y)$.

These are defined analogously to the one-dimensional case.

according to Chapter 2 (for discrete value random variables).
bzw. Chapter 3 (for continuous value random variables):

$\text{Definition:}$ For the (non-centered) moments the relation holds:

$$m_{kl}={\rm E}\big[x^k\cdot y^l\big]=\int_{-\infty}^{+\infty}\hspace{0.2cm}\int_{-\infty}^{+\infty} x\hspace{0.05cm}^{k} \cdot y\hspace{0.05cm}^{l} \cdot f_{xy}(x,y) \, {\rm d}x\, {\rm d}y.$$

Thus, the two linear means are $m_x = m_{10}$ and $m_y = m_{01}.$

$\text{definition:}$ The $m_x$ and $m_y$ related central moments respectively are:

$$\mu_{kl} = {\rm E}\big[(x-m_{x})\hspace{0.05cm}^k \cdot (y-m_{y})\hspace{0.05cm}^l\big] .$$

In this general definition equation, the variances $σ_x^2$ and $σ_y^2$ of the two individual components are included by $\mu_{20}$ and $\mu_{02}$ respectively.

$\text{Definition:}$ Of particular importance is the covariance $(k = l = 1)$, which is a measure of the linear statistical dependence between the random variables $x$ and $y$ :

$$\mu_{11} = {\rm E}\big[(x-m_{x})\cdot(y-m_{y})\big] = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} (x-m_{x}) \cdot (y-m_{y})\cdot f_{xy}(x,y) \,{\rm d}x \, {\rm d}y .$$

In the following, we also denote the covariance $\mu_{11}$ in part by $\mu_{xy}$, if the covariance refers to the random variables $x$ and $y$

Notes:

The covariance $\mu_{11}=\mu_{xy}$ is related to the non-centered moment $m_{11} = m_{xy} = {\rm E}\big[x \cdot y\big]$ as follows:

$$\mu_{xy} = m_{xy} -m_{x }\cdot m_{y}.$$

This equation is enormously advantageous for numerical evaluations, since $m_{xy}$, $m_x$ and $m_y$ can be found from the sequences $〈x_v〉$ and $〈y_v〉$ in a single run.
On the other hand, if one were to calculate the covariance $\mu_{xy}$ according to the above definition equation, one would have to find the mean values $m_x$ and $m_y$ in a first run and could then only calculate the expected value ${\rm E}\big[(x - m_x) \cdot (y - m_y)\big]$ in a second run.

Example 2D expected values

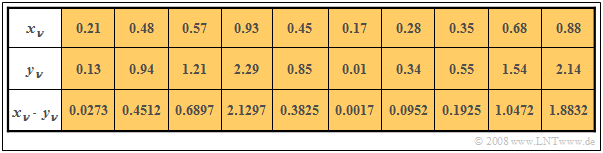
$\text{Example 4:}$ In the first two rows of the table, the respective first elements of two random sequences $〈x_ν〉$ and $〈y_ν〉$ are entered. In the last row, the respective products $x_ν - y_ν$ are given.

By averaging over the ten sequence elements in each case, one obtains

$$m_x =0.5,\ \ m_y = 1, \ \ m_{xy} = 0.69.$$

This directly results in the value for the covariance:

$$\mu_{xy} = 0.69 - 0.5 · 1 = 0.19.$$

Without knowledge of the equation $\mu_{xy} = m_{xy} - m_x\cdot m_y$ one would have had to first determine the mean values $m_x$ and $m_y$ in the first run,
in order to then determine the covariance $\mu_{xy}$ as the expected value of the product of the mean-free variables in a second run.

Correlation coefficient

With statistical independence of the two components $x$ and $y$ the covariance $\mu_{xy} \equiv 0$. This case has already been considered in $\text{Example 2}$ on the WDF and VTF for statistically independent components page.

But the result $\mu_{xy} = 0$ is also possible for statistically dependent components $x$ and $y$ namely when they are uncorrelated, i.e. linearly independent .
The statistical dependence is then not of first order, but of higher order, for example corresponding to the equation $y=x^2.$

One speaks of complete correlation when the (deterministic) dependence between $x$ and $y$ is expressed by the equation $y = K · x$ . Then the covariance is given by:

$\mu_{xy} = σ_x · σ_y$ with positive value of $K$,
$\mu_{xy} = - σ_x · σ_y$ with negative $K$–value.

Therefore, instead of covariance, one often uses the so-called correlation coefficient as a descriptive variable.

$\text{Definition:}$ The correlation coefficient is the quotient of the covariance $\mu_{xy}$ and the product of the rms values $σ_x$ and $σ_y$ of the two components:

$$\rho_{xy}=\frac{\mu_{xy} }{\sigma_x \cdot \sigma_y}.$$

The correlation coefficient $\rho_{xy}$ has the following properties:

Because of normalization, $-1 \le ρ_{xy} ≤ +1$ always holds.
If the two random variables $x$ and $y$ are uncorrelated, then $ρ_{xy} = 0$.
For strict linear dependence between $x$ and $y$ is $ρ_{xy}= ±1$ ⇒ complete correlation.
A positive correlation coefficient means that when $x$ is larger, on statistical average $y$ is also larger than when $x$ is smaller.
In contrast, a negative correlation coefficient expresses that $y$ becomes smaller on average as $x$ increases.

Gaussian 2D WDF with correlation

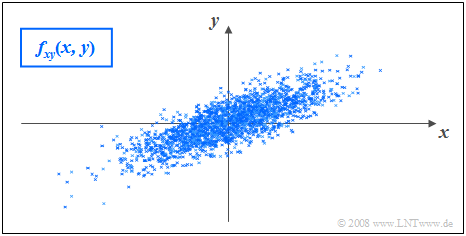
$\text{Example 5:}$ The following conditions apply:

The considered components $x$ and $y$ each have a Gaussian WDF.
The two scatterers are different $(σ_y < σ_x)$.
The correlation coefficient is $ρ_{xy} = 0.8$.

Unlike the Example 2 with statistically independent components ⇒ $ρ_{xy} = 0$ $($drotz $σ_y < σ_x)$ one recognizes that here with larger $x$-value on statistical average also $y$ is larger than with smaller $x$.

Korrelationsgerade

Gaußsche 2D WDF mit Korrelationsgerade

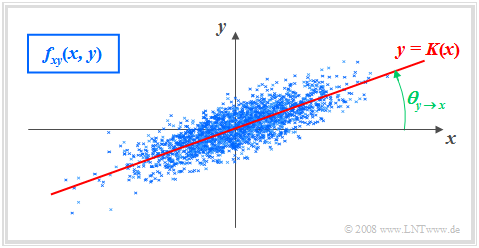
$\text{Definition:}$ Als Korrelationsgerade bezeichnet man die Gerade $y = K(x)$ in der $(x, y)$–Ebene durch den „Mittelpunkt” $(m_x, m_y)$. Manchmal wird diese Gerade auch Regressionsgerade genannt.

Die Korrelationsgerade besitzt folgende Eigenschaften:

Die mittlere quadratische Abweichung von dieser Geraden – in $y$–Richtung betrachtet und über alle $N$ Punkte gemittelt – ist minimal:

$$\overline{\varepsilon_y^{\rm 2} }=\frac{\rm 1}{N} \cdot \sum_{\nu=\rm 1}^{N}\; \;\big [y_\nu - K(x_{\nu})\big ]^{\rm 2}={\rm Minimum}.$$

Die Korrelationsgerade kann als eine Art „statistische Symmetrieachse“ interpretiert werden. Die Geradengleichung lautet:

$$y=K(x)=\frac{\sigma_y}{\sigma_x}\cdot\rho_{xy}\cdot(x - m_x)+m_y.$$

Der Winkel, den die Korrelationsgerade zur $x$–Achse einnimmt, beträgt:

$$\theta_{y\hspace{0.05cm}\rightarrow \hspace{0.05cm}x}={\rm arctan}\ (\frac{\sigma_{y} }{\sigma_{x} }\cdot \rho_{xy}).$$

Durch diese Nomenklatur soll deutlich gemacht werden, dass es sich hier um die Regression von $y$ auf $x$ handelt.

Die Regression in Gegenrichtung – also von $x$ auf $y$ – bedeutet dagegen die Minimierung der mittleren quadratischen Abweichung in $x$–Richtung.

Das interaktive Applet Korrelationskoeffizient und Regressionsgerade verdeutlicht, dass sich im Allgemeinen $($falls $σ_y \ne σ_x)$ für die Regression von $x$ auf $y$ ein anderer Winkel und damit auch eine andere Regressionsgerade ergeben wird:

$$\theta_{x\hspace{0.05cm}\rightarrow \hspace{0.05cm} y}={\rm arctan}\ (\frac{\sigma_{x}}{\sigma_{y}}\cdot \rho_{xy}).$$