General Description of Linear Block Codes

1 Linear codes and cyclic codes
2 Code definition by the parity-check matrix
3 Code definition by the generator matrix
4 Identical Codes
5 Systematische Codes
6 Zusammenhang zwischen Generator– und Prüfmatrix
7 Generatormatrix vs. Prüfmatrix bei systematischen Codes
8 Darstellung von SPC und RC als duale Codes
9 Einige Eigenschaften des (7, 4, 3)–Hamming–Codes
10 Aufgaben zum Kapitel

Linear codes and cyclic codes

All codes mentioned so far,

the single parity-check code,
the repetition code and
the Hamming code

are linear. Now the definition of linearity valid for binary block codes is added.

$\text{Definition:}$ A linear binary block code $\mathcal{C}$ is a set of $2^k$ code words $\underline{x}= (x_1, x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, x_n)$, where the (modulo 2) sum of any two code words $\underline{x}$ and $\underline{x}\hspace{0.05cm}'$ again gives a valid code word:

\[\underline{x}, \underline{x}\hspace{0.05cm}' \in {\rm GF}(2^n),\hspace{0.3cm} \underline{x}, \underline{x}\hspace{0.05cm}' \in \mathcal{C} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\underline{x} + \underline{x}\hspace{0.05cm}' \in \mathcal{C} \hspace{0.05cm}.\]

This condition must also be satisfied for $\underline{x} = \underline{x}\hspace{0.05cm}'$ .

Hint: For the remainder of this book, modulo addition will no longer be expressed by the modulo addition sign to simplify notation, but by the conventional plus sign.

$\text{Example 1:}$ We consider two $\text{(3, 2)}$ block codes:

\[\mathcal{C}_1 = \{ (0, 0, 0) \hspace{0.05cm}, (0, 1, 1) \hspace{0.05cm},(1, 0, 1) \hspace{0.05cm},(1, 1, 0) \}\hspace{0.05cm},\]

\[\mathcal{C}_2 = \{ (0, 0, 0) \hspace{0.05cm}, (0, 1, 1) \hspace{0.05cm},(1, 1, 0) \hspace{0.05cm},(1, 1, 1) \hspace{0.05cm}.\]

You can see:

The code $\mathcal{C}_1$ is linear, since the modulo 2 addition of any two code words always yields also a valid code word, e.g. $(0, 1, 1) + (1, 0, 1) = (1, 1, 0)$.

The above definition also applies to the modulo 2 addition of a code word with itself, for example. $(0, 1, 1) + (0, 1, 1) = (0, 0, 0)$
⇒ Each linear code contains the all-zero word $\underline{0}$.

Although the last condition is satisfied, $\mathcal{C}_2$ is not a linear code. Indeed, for this code, for example: $(0, 1, 1) + (1, 1, 0) = (1, 0, 1)$. This is not a valid code word of $\mathcal{C}_2$.

In the following, we restrict ourselves exclusively to linear codes, since nonlinear codes are of secondary importance for practical use.

$\text{Definition:}$ A linear block code $\mathcal{C}$ is called cyclic if every cyclic shift of a code word $\underline{x}$ (to the left or right) results in a valid code word:

\[\underline{x}= (x_1, x_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, x_n) \in \mathcal{C} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\underline{x}\hspace{0.05cm}'= (x_n, x_1, \hspace{0.05cm}\text{...} \hspace{0.05cm} \hspace{0.05cm}, x_{n-1}) \in \mathcal{C} \hspace{0.05cm}.\]

Code table of the systematic $\text{(7, 4, 3)}$ Hamming codes;
black: $k= 4$ Information bits, rot: $n-k = 3$ parity-check bits

$\text{Example 2:}$

You can see from the table for the $\text{HC (7, 4, 3)}$ that it is linear and cyclic.
A valid code word results even if all bits are inverted: $0 ↔ 1$.
Also the $\underline{0}$–word ($n$ times a "zero") and the $\underline{1}$–word ($n$ times a "one") are allowed with this code.

Code definition by the parity-check matrix

$\text{(7, 4, 3)}$ Hamming code

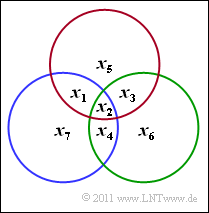
We consider the $\text{(7, 4, 3)}$ Hamming code with code words $\underline{x}$ of length $n=7$, consisting of.

$k = 4$ information bits $x_1$, $x_2$, $x_3$, $x_4$, and
$m = n-k = 3$ parity-check bits $x_5$, $x_6$, $x_7$.

Thus, the parity-check equations are:

\[x_1 + x_2 + x_3 + x_5 = 0 \hspace{0.05cm},\]

\[x_2 + x_3 + x_4 + x_6 = 0 \hspace{0.05cm},\]

\[x_1 + x_2 + x_4 + x_7 = 0 \hspace{0.05cm}. \]

In matrix notation, this set of equations reads:

\[{ \boldsymbol{\rm H}} \cdot \underline{x}^{\rm T}= \underline{0}^{\rm T} \hspace{0.05cm}. \]

In this equation are used:

the parity-check matrix ${ \boldsymbol{\rm H}}$ with $m = n-k = 3$ rows and $n = 7$ columns:

\[{ \boldsymbol{\rm H}} = \begin{pmatrix} 1 &1 &1 &0 &1 & 0 & 0\\ 0 &1 &1 &1 &0 & 1 & 0\\ 1 &1 &0 &1 &0 & 0 & 1 \end{pmatrix}\hspace{0.05cm},\]

the code word $\underline{x}= (x_1, x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm}, x_7)$ of length $n = 7$,

the all-zero vector $\underline{0} = (0, 0, 0)$ of length $m = 3$.

By transposing, the row vectors $\underline{x}$ and $\underline{0}$ become the corresponding column vectors $\underline{x}^{\rm T}$ and $\underline{0}^{\rm T}$.

$\text{(6, 3, 3)}$ block code

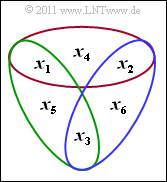
$\text{Example 3:}$ The graph illustrates the $m = 3$ parity-check equations of a code $\mathcal{C}$ with code parameters $n = 6$ and $k = 3$ in the order red, green and blue. Thus, it is not a Hamming code $(n \ne 2^m-1)$.

According to the equation $\boldsymbol{\rm H} \cdot \underline{x}^{\rm T}= \underline{0}^{\rm T}$ the parity-check matrix is:

\[ \boldsymbol{\rm H} = \begin{pmatrix} 1 &1 &0 &1 &0 & 0\\ 1 &0 &1 &0 &1 & 0\\ 0 &1 &1 &0 &0 & 1 \end{pmatrix}\hspace{0.05cm}.\]

The $2^k = 8$ code words in systematic realization are (with the parity-check bits to the right of the small arrow):

\[\underline{x}_0 = (0, 0, 0_{\hspace{0.01cm} \rightarrow} 0, 0, 0)\hspace{0.05cm}, \hspace{0.5cm} \underline{x}_1 = (0, 0, 1_{\hspace{0.01cm} \rightarrow}0, 1, 1)\hspace{0.05cm},\hspace{0.5cm} \underline{x}_2 = (0, 1, 0_{\hspace{0.01cm} \rightarrow}1, 0, 1)\hspace{0.05cm},\hspace{0.5cm}\underline{x}_3 = (0, 1, 1_{\hspace{0.01cm} \rightarrow}1, 1, 0)\hspace{0.05cm}, \] \[\underline{x}_4 = (1, 0, 0_{\hspace{0.01cm} \rightarrow} 1, 1, 0)\hspace{0.05cm}, \hspace{0.5cm} \underline{x}_5 = (1, 0, 1_{\hspace{0.01cm} \rightarrow}1, 0, 1)\hspace{0.05cm},\hspace{0.5cm} \underline{x}_6 = (1, 1, 0_{\hspace{0.01cm} \rightarrow}0, 1, 1)\hspace{0.05cm}, \hspace{0.5cm} \underline{x}_7 = (1, 1, 1_{\hspace{0.01cm} \rightarrow}0, 0, 0)\hspace{0.05cm}.\]

It can be seen from these specifications:

The number of columns $\boldsymbol{\rm H}$ is equal to the code length $n$.

The number of lines of $\boldsymbol{\rm H}$ is equal to the number $m = n-k$ of parity-check equations.

From $\boldsymbol{\rm H} \cdot \underline{x}^{\rm T}= \underline{0}^{\rm T} $ it therefore does not follow that all codewords contain an even number of ones.

Code definition by the generator matrix

The check matrix $\boldsymbol{\rm H}$ of a $(n, k)$–block code has $m = n-k$ rows and $n$ columns. However, the same code can be described by the matrix $\boldsymbol{\rm G}$ with also $n$ columns, but $k$ rows:

$\text{Definition:}$ A linear binary block code $\mathcal{C}$ can be characterized by the check matrix' $\boldsymbol{\rm H}$ or with the generator matrix' $\boldsymbol{\rm G}$ as follows:

\[\mathcal{C} = \{ \underline{x} \in {\rm GF}(2^n)\text{:} \hspace{0.2cm}{ \boldsymbol{\rm H} } \cdot \underline{x}^{\rm T}= \underline{0}^{\rm T} \}\hspace{0.05cm},\]

\[\mathcal{C} = \{ \underline{x} \in {\rm GF}(2^n)\hspace{0.05cm}, \hspace{0.1cm}\underline{u} \in {\rm GF}(2^k)\text{:} \hspace{0.2cm}\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G} } \}\hspace{0.05cm}.\]

Before we turn to the properties of the generator matrix, we describe the generation of the code words with an example.

$\text{Example 4:}$ We consider a linear $(5, 3)$ block code with the generator matrix (again, this is not a Hamming code)

\[ \boldsymbol{\rm G} = \begin{pmatrix} 1 &1 &0 &1 &1\\ 0 &1 &0 &1 &0\\ 0 &1 &1 &1 &0 \end{pmatrix} = \begin{pmatrix} \underline{g}_1\\ \underline{g}_2\\ \underline{g}_3\\ \end{pmatrix} \hspace{0.05cm}.\]

Thus, the information words $\underline{u}= (u_1, u_2, u_3)$ are assigned to the code words $\underline{x}= (x_1, x_2, x_3, x_4, x_5)$ according to the following equations.
The following always applies $\underline{x} = \underline{u} \cdot \boldsymbol{\rm G}$:

\[\underline{u}_0 = (0, 0, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_0 = (0, 0, 0, 0, 0) \hspace{0.05cm},\]

\[\underline{u}_1 = (0, 0, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_1 = (0, 1, 1, 1, 0) \hspace{0.1cm}= \hspace{0.1cm}\underline{g}_3\hspace{0.05cm},\]

\[\underline{u}_2 = (0, 1, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_2 = (0, 1, 0, 1, 0)\hspace{0.1cm}= \hspace{0.1cm} \underline{g}_2\hspace{0.05cm},\]

\[\underline{u}_3 = (0, 1, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_3 = (0, 0, 1, 0, 0) \hspace{0.1cm}= \hspace{0.1cm} \underline{g}_2+\underline{g}_3\hspace{0.05cm},\]

\[\underline{u}_4 = (1, 0, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_4 = (1, 1, 0, 1, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{g}_1 \hspace{0.05cm},\]

\[\underline{u}_5 =(1, 0, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_5 = (1, 0, 1, 0, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{g}_1+\underline{g}_3\hspace{0.05cm},\]

\[\underline{u}_6 = (1, 1, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_6 = (1, 0, 0, 0, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{g}_1+\underline{g}_2\hspace{0.05cm},\]

\[\underline{u}_7 =(1, 1, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}_7 = (1, 1, 1, 1, 1) \hspace{0.1cm}= \hspace{0.1cm} \underline{g}_1+ \underline{g}_2+\underline{g}_3\hspace{0.05cm}.\]

Notes:

The basis vectors used here for the calculation $\underline{g}_1$, $\underline{g}_2$ and $\underline{g}_3$ – each with length $n = 5$ – correspond to the $k = 3$ rows of the generator matrix $\boldsymbol{\rm G}$.
This code is neither suitable for error correction nor for error detection because of $d_{\rm min} = 1$ . Nevertheless, this code is also considered exemplarily on the next pages, because the coding results are well interpretable.
At this point we would like to draw your attention to the applet Gram–Schmidt process for the book "Digital Signal Transmission", which teaches the calculation of basis functions, although in a different context than the one used here.

Identical Codes

The vectors used in $\text{Example 4}$ on the last page $\underline{g}_1$, $\underline{g}_2$, ... , $\underline{g}_k$ are the basis vectors of the linear block code. $\mathcal{C}$.

The code itself can be viewed as a $k$–dimensionaler subspace of $\text{GF}(2^n)$ .
The basis vectors $\underline{g}_1$, $\underline{g}_2$, ... , $\underline{g}_k$ are linearly independent.

However, the subspace $\mathcal{C}$ is not only spanned by the basis vectors

\[\underline{g}_1 = (1, 1, 0, 1, 1) \hspace{0.05cm},\hspace{0.3cm} \underline{g}_2 = (0, 1, 0, 1, 0) \hspace{0.05cm},\hspace{0.3cm} \underline{g}_3 = (0, 1, 1, 1, 0) \hspace{0.05cm}\]

but other basis vectors $\underline{g}\hspace{0.05cm}'_1$, $\underline{g}\hspace{0.05cm}'_2$ and $\underline{g}\hspace{0.05cm}'_3$ are equally suitable as long as linear independence is guaranteed between them.

$\text{Example 5:}$ We compare the code $\mathcal{C}$ of $\text{Example 4}$ with a second code $\mathcal{C}\hspace{0.05cm}'$. The generator matrices are:

\[ \boldsymbol{\rm G} = \begin{pmatrix} \underline{g}_1\\ \underline{g}_2\\ \underline{g}_3\\ \end{pmatrix}= \begin{pmatrix} 1 &1 &0 &1 &1\\ 0 &1 &0 &1 &0\\ 0 &1 &1 &1 &0 \end{pmatrix}\hspace{0.05cm},\hspace{0.3cm} \boldsymbol{\rm G}\hspace{0.05cm}' = \begin{pmatrix} \underline{g}\hspace{0.05cm}'_1\\ \underline{g}\hspace{0.05cm}'_2\\ \underline{g}\hspace{0.05cm}'_3\\ \end{pmatrix}= \begin{pmatrix} 1 &0 &0 &0 &1\\ 0 &1 &0 &1 &0\\ 0 &0 &1 &0 &0 \end{pmatrix}\hspace{0.05cm}.\]

The two codes are identical: They contain the exact same code words; only a different assignment applies.
During the transition from $\boldsymbol{\rm G}$ to $\boldsymbol{\rm G}\hspace{0.05cm}'$, the following allowed operations were performed:

\[\underline{g}\hspace{0.05cm}'_1 = \underline{g}_1 + \underline{g}_2 \hspace{0.05cm},\hspace{0.3cm} \underline{g}\hspace{0.05cm}'_2 = \underline{g}_2 \hspace{0.05cm},\hspace{0.3cm} \underline{g}\hspace{0.05cm}'_3 = \underline{g}_2 + \underline{g}_3 \hspace{0.05cm}.\]

The corresponding code $\mathcal{C}'$ is obtained by the equation $\underline{x}' = \underline{u} \cdot \boldsymbol{\rm G}'$:

\[\underline{u}_0 = (0, 0, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_0 = (0, 0, 0, 0, 0) \hspace{0.1cm}= \hspace{0.1cm} \underline{x}_0 \hspace{0.05cm},\]

\[\underline{u}_1 = (0, 0, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_1 = (0, 0, 1, 0, 0) \hspace{0.1cm}= \hspace{0.1cm}\underline{x}_3\hspace{0.05cm},\]

\[\underline{u}_2 = (0, 1, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_2 = (0, 1, 0, 1, 0) \hspace{0.1cm}= \hspace{0.1cm} \underline{x}_2\hspace{0.05cm},\]

\[\underline{u}_3 = (0, 1, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_3 = (0, 1, 1, 1, 0) \hspace{0.1cm}= \hspace{0.1cm} \underline{x}_1\hspace{0.05cm},\]

\[\underline{u}_4 = (1, 0, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_4 = (1, 0, 0, 0, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{x}_6 \hspace{0.05cm},\]

\[\underline{u}_5 =(1, 0, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_5 = (1, 0, 1, 0, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{x}_5\hspace{0.05cm},\]

\[\underline{u}_6 = (1, 1, 0)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_6 = (1, 1, 0, 1, 1)\hspace{0.1cm}= \hspace{0.1cm} \underline{x}_4\hspace{0.05cm},\]

\[\underline{u}_7 = (1, 1, 1)\hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm}'_7 = (1, 1, 1, 1, 1) \hspace{0.1cm}= \hspace{0.1cm} \underline{x}_7\hspace{0.05cm}.\]

The corresponding code words $\underline{x}_i = \underline{u}_i \cdot \boldsymbol{\rm G}$ of the code $\mathcal{C}$ ⇒ generator matrix $\boldsymbol{\rm G}$ are give in $\text{Example 4}$ (previous page).

$\text{Conclusion:}$ The code tables of $\text{Example 4}$ and $\text{Example 5}$ make clear:

$\mathcal{C}$ and $\mathcal{C}\hspace{0.05cm}'$ contain the same code words. They are thus identical codes and both have the same capability of correction(see next page).

$\mathcal{C}\hspace{0.05cm}'$ is now a systematic code since the first $k$ binary digits of each codeword $\underline{x}\hspace{0.05cm}'_i$ match the binary digits of the information word.

Systematische Codes

Die Eigenschaft "systematisch" soll nun noch in mathematischer Form angegeben werden.

$\text{Definition:}$ Bei einem $\text{systematischen }(n, k)–\text{Blockcode} \ \ \mathcal{C}$ beinhaltet jedes Codewort $\underline{x}$ explizit das Informationswort $\underline{u}$.

Das heißt, es gilt: $\underline{u} = (u_1, u_2, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_k) \hspace{0.3cm} \rightarrow\hspace{0.3cm} \underline{x}\hspace{0.05cm} = (u_1, u_2, ... \hspace{0.05cm}, u_k, x_{k+1}, \hspace{0.05cm}\text{...}\hspace{0.05cm}, x_n)\hspace{0.05cm}.$

Die Generatormatrix hat in diesem Fall die Form $\boldsymbol{\rm G_{\rm sys} } =\left({ \boldsymbol{\rm I}_{\rm k} \ ; \ \boldsymbol{\rm P} }\right)$ mit der $k×k$–Einheitsmatrix $\boldsymbol{\rm I}_{\rm k}$ und einer geeignet zu wählenden $(n-1)×k$–Matrix $\boldsymbol{\rm P}$.

Für das $\text{Beispiel 5}$ auf der letzten Seite kann also auch geschrieben werden:

\[ \boldsymbol{\rm G_{sys}} =\left({ \boldsymbol{\rm I}}_3 \: ; \: { \boldsymbol{\rm P}}\right)\hspace{0.3cm}{\rm mit}\hspace{0.3cm} { \boldsymbol{\rm I_{3}}} = \begin{pmatrix} 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \end{pmatrix}\hspace{0.3cm}{\rm und}\hspace{0.3cm} { \boldsymbol{\rm P}} = \begin{pmatrix} 0 &1 \\ 1 &0 \\ 0 &0 \end{pmatrix}\hspace{0.05cm}.\]

Erfreulich aus Sicht der Kanalcodierung ist, dass für jeden Code $\mathcal{C}$ ein systematischer (identischer oder zumindest äquivalenter) Code $\mathcal{C}_{\rm sys}$ gefunden werden kann.

Beim identischen systematischen Code beinhalten $\underline{x}$ und $\underline{x}_{\rm sys}$ die gleichen Codeworte, nur die Zuordnung $\underline{u} → \underline{x}$ ist unterschiedlich. Man kommt durch folgende Manipulationen bezüglich der Generatormatrix $\boldsymbol{\rm G}$ von einem Blockcode $\mathcal{C}$ zum identischen systematischen Code $\mathcal{C}_{\rm sys}$:

Vertauschen oder Permutieren der Zeilen,

Multiplizieren aller Zeilen mit einem konstanten Vektor ungleich $\underline{0}$,

Ersetzen einer Zeile durch eine Linearkombination zwischen dieser Zeile und einer anderen.

$\text{Ohne Beweis:}$ Ein $\text{identischer systematischer Code }\mathcal{C}_{\rm sys}$ kann immer dann gefunden werden, wenn zu einer Generatormatrix $\boldsymbol{\rm G}$ eine Matrix $\boldsymbol{\rm A}$ existiert, so dass $\boldsymbol{\rm G}_{\rm sys} = \boldsymbol{\rm A} \cdot \boldsymbol{\rm G}$ gilt.

Ist dies nicht möglich, so findet man zumindest durch Vertauschen oder Permutieren der Spalten von $\boldsymbol{\rm G}$ einen äquivalenten systematischen Code:

\[\mathcal{C}_{\rm sys} = {\rm \pi} (\mathcal{C})\hspace{0.3cm}{\rm mit}\hspace{0.3cm}{\rm \pi}():\hspace{0.15cm}{\rm Permutationsoperator}\hspace{0.05cm}.\]

Die Codes $\mathcal{C}$ und $\mathcal{C}_{\rm sys}$ beinhalten dann zwar andere Codeworte, aber sie zeigen gleiche Eigenschaften. Beispielsweise weist $\mathcal{C}_{\rm sys}$ in diesem Fall die gleiche minimale Hamming–Distanz $d_{\rm min}$ auf wie der Code $\mathcal{C}$.

$\text{Beispiel 6:}$ Wir betrachten die Generatormatrizen

\[ \boldsymbol{\rm G} = \begin{pmatrix} 1 &1 &0 &0 \\ 0 &0 &1 &1 \end{pmatrix}\hspace{0.3cm}{\rm und}\hspace{0.3cm} \boldsymbol{\rm G_{sys} } = \begin{pmatrix} 1 &0 &1 &0 \\ 0 &1 &0 &1 \end{pmatrix}\hspace{0.05cm}.\]

Die Analyse zeigt:

Die zugehörigen Codes $\mathcal{C}$ und $\mathcal{C}_{\rm sys}$ beinhalten unterschiedliche Codeworte und sind somit auch nicht identisch:

\[\mathcal{C} = \big \{ (0, 0, 0, 0) \hspace{0.05cm}, (0, 0, 1, 1) \hspace{0.05cm},(1, 1, 0, 0) \hspace{0.05cm},(1, 1, 1, 1) \big \}\hspace{0.05cm},\]

\[\mathcal{C}_{\rm sys}= \big \{ (0, 0, 0, 0) \hspace{0.05cm}, (0, 1, 0, 1) \hspace{0.05cm},(1, 0, 1, 0) \hspace{0.05cm},(1, 1, 1, 1) \big \}\hspace{0.05cm}.\]

Aber sie sind äquivalent: $\boldsymbol{\rm G}_{\rm sys}$ ergibt sich aus $\boldsymbol{\rm G}$ durch Vertauschen der zweiten und dritten Spalte.
Es handelt sich in beiden Fällen um einen $\text{(4, 2, 2)}$–Blockcode ⇒ $d_{\rm min} = 2$.

Zusammenhang zwischen Generator– und Prüfmatrix

Zur Definition dieser beiden Beschreibungsmatrizen gehen wir von folgenden Gleichungen aus:

\[\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{x}^{\rm T} = { \boldsymbol{\rm G}}^{\rm T} \cdot \underline{u}^{\rm T} \hspace{0.05cm}, \hspace{0.8cm} { \boldsymbol{\rm H}} \cdot \underline{x}^{\rm T} = { \boldsymbol{\rm 0}}\hspace{0.05cm}.\]

Verknüpft man diese zwei Gleichungen, so erhält man:

\[{ \boldsymbol{\rm H}} \cdot { \boldsymbol{\rm G}}^{\rm T} \cdot \underline{u}^{\rm T} = \underline{0}\hspace{0.5cm} \forall \hspace{0.15cm}\underline{u} \in {\rm GF}(2^k)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} { \boldsymbol{\rm H}} \cdot { \boldsymbol{\rm G}}^{\rm T} = { \boldsymbol{\rm 0}} \hspace{0.05cm}.\]

Anzumerken ist, dass in diesen Gleichungen

$\underline{0}$ einen Zeilenvektor mit $k$ Elementen bezeichnet und
$\boldsymbol{\rm 0}$ eine Matrix mit $m$ Zeilen und $k$ Spalten angibt,

wobei alle Elemente von $\underline{0}$ und $\boldsymbol{\rm 0}$ identisch Null sind.

$\text{Beispiel 7:}$ Wir betrachten wie im $\text{Beispiel 4}$ den $\text{(5, 3)}$–Blockcode

\[\mathcal{C} = \big \{ \hspace{0.15cm} ( \hspace{0.05cm} 0, 0, 0, 0, 0) \hspace{0.05cm},\]

\[ \hspace{0.6cm}( \hspace{0.05cm} 0, 1, 1, 1, 0) \hspace{0.05cm},\]

\[ \hspace{0.6cm}( \hspace{0.05cm}0, 1, 0, 1, 0) \hspace{0.05cm},\]

\[ \hspace{0.6cm}( \hspace{0.05cm}0, 0, 1, 0, 0) \hspace{0.05cm},\]

\[ \hspace{0.6cm}( \hspace{0.05cm} 1, 1, 0, 1, 1) \hspace{0.05cm},\]

\[ \hspace{0.6cm}( \hspace{0.05cm}1, 0, 1, 0, 1) \hspace{0.05cm},\]

\[ \hspace{0.6cm}( \hspace{0.05cm}1, 0, 0, 0, 1) \hspace{0.05cm},\]

\[ \hspace{0.6cm}(\hspace{0.05cm}1, 1, 1, 1, 1) \big \}\hspace{0.05cm}.\]

Aus $n= 5$ und $k = 3$ folgt für die Anzahl der Prüfgleichungen $m = 2$. Durch Analyse der möglichen Codeworte erhält man folgende Ergebnisse:

\[x_1 \oplus x_5 = 0 \hspace{0.05cm},\hspace{0.5cm} x_2 \oplus x_4 = 0\hspace{1cm} \Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm H} } = \begin{pmatrix} 1 &0 &0 &0 &1\\ 0 &1 &0 &1 &0 \end{pmatrix}\]

\[\Rightarrow \hspace{0.3cm} { \boldsymbol{\rm H} } \cdot { \boldsymbol{\rm G} }^{\rm T} = \begin{pmatrix} 1 &0 &0 &0 &1\\ 0 &1 &0 &1 &0 \end{pmatrix} \begin{pmatrix} 1 &0 &0 \\ 1 &1 &1 \\ 0 &0 &1 \\ 1 &1 &1 \\ 1 &0 &0 \end{pmatrix} = \begin{pmatrix} 0 &0 &0 \\ 0 &0 &0 \end{pmatrix}\hspace{0.05cm}.\]

Die Nullmatrix besteht hier aus $m = 2$ Zeilen und $k = 3$ Spalten. Beispielsweise gilt für das Element in der ersten Zeile und der ersten Spalte:

\[1 \cdot 1 \hspace{0.05cm}\oplus \hspace{0.05cm} 0 \cdot 1 \hspace{0.05cm}\oplus \hspace{0.05cm} 0 \cdot 0 \hspace{0.05cm}\oplus \hspace{0.05cm} 0 \cdot 1 \hspace{0.05cm}\oplus \hspace{0.05cm} 1 \cdot 1 = 0 \hspace{0.05cm}.\]

Generatormatrix vs. Prüfmatrix bei systematischen Codes

Im allgemeinen Fall können $\boldsymbol{\rm G}$ und $\boldsymbol{\rm H}$ nicht direkt ineinander umgerechnet werden, schon allein aufgrund der unterschiedlichen Dimensionen von Generatormatrix $(k \times n)$ und Prüfmatrix $(m \times n)$.

$\text{Ohne Beweis:}$ Der Rechengang vereinfacht sich, wenn die $(k \times n)$ –Generatormatrix in systematischer Form vorliegt: $ \boldsymbol{\rm G_{sys} } =\left({ \boldsymbol{\rm I} }_k \: ; \: { \boldsymbol{\rm P} }\right)$. Dann folgt aus $\boldsymbol{\rm H} \cdot \boldsymbol{\rm G}^{\rm T} = \boldsymbol{\rm 0}$ für die $(m \times n)$–Prüfmatrix mit $m = n-k$:

\[{ \boldsymbol{\rm H} } =\left( - { \boldsymbol{\rm P} }^{\rm T} \: ; \: { \boldsymbol{\rm I} }_m \right) \hspace{0.05cm}.\]

Diese Gleichung gilt allgemein, also auch im nichtbinären Fall. Da wir uns im gesamten ersten Hauptkapitel auf binäre Codes beschränken ⇒ $\mathcal{C} \in \text{GF}(2^n)$, gilt $ - \boldsymbol{\rm P} = +\boldsymbol{\rm P}$, und man erhält die Form, die wir im Weiteren verwenden.

\[{ \boldsymbol{\rm H} } =\left( - { \boldsymbol{\rm P} }^{\rm T} \: ; \: { \boldsymbol{\rm I} }_m \right)=\left( { \boldsymbol{\rm P} }^{\rm T} \: ; \: { \boldsymbol{\rm I} }_m \right)\hspace{0.05cm}. \]

$\text{Beispiel 8:}$ Wir betrachten weiterhin den beispielhaften $\text{(5, 3)}$–Blockcode, gehen aber nun von der systematischen Generatormatrix $\boldsymbol{\rm G}_{\rm sys}$ aus, die wir im $\text{Beispiel 5}$ ermittelt haben:

\[ \boldsymbol{\rm G_{sys} } = \begin{pmatrix} 1 &0 &0 &0 &1\\ 0 &1 &0 &1 &0\\ 0 &0 &1 &0 &0 \end{pmatrix} =\left({ \boldsymbol{\rm I} }_3 \: ; \: { \boldsymbol{\rm P} }\right) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} { \boldsymbol{\rm I_3} }= \begin{pmatrix} 1 &0 &0 \\ 0 &1 &0\\ 0 &0 &1 \end{pmatrix}, \hspace{0.3cm} { \boldsymbol{\rm P} }= \begin{pmatrix} 0 &1 \\ 1 &0\\ 0 &0 \end{pmatrix} \hspace{0.3cm}\Rightarrow\hspace{0.3cm} { \boldsymbol{\rm P}^{\rm T} } = \begin{pmatrix} 0 &1 &0\\ 1 &0 &0 \end{pmatrix}\hspace{0.05cm}.\]

Damit erhält man für die Prüfmatrix

\[{ \boldsymbol{\rm H} } =\left({ \boldsymbol{\rm P} }^{\rm T} \: ; \: { \boldsymbol{\rm I} }_2 \right) = \begin{pmatrix} 0 &1 &0 &1 &0\\ 1 &0 &0 &0 &1 \end{pmatrix} \hspace{0.05cm},\]

und es ergibt sich folgende Codetabelle:

\[\underline{u}_0 = (0, 0, 0)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_0 = (0, 0, 0, 0, 0) \hspace{0.05cm},\hspace{0.8cm}\underline{u}_4 = (1, 0, 0)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_4 = (1, 0, 0, 0, 1) \hspace{0.05cm},\]

\[\underline{u}_1 = (0, 0, 1)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_1 = (0, 0, 1, 0, 0) \hspace{0.05cm},\hspace{0.8cm}\underline{u}_5 =(1, 0, 1)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_5 = (1, 0, 1, 0, 1)\hspace{0.05cm},\]

\[\underline{u}_2 =(0, 1, 0)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_2 = (0, 1, 0, 1, 0) \hspace{0.05cm},\hspace{0.8cm}\underline{u}_6 =(1, 1, 0)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_6 = (1, 1, 0, 1, 1)\hspace{0.05cm},\]

\[\underline{u}_3 = (0, 1, 1)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_3 = (0, 1, 1, 1, 0) \hspace{0.05cm},\hspace{0.8cm}\underline{u}_7 = (1, 1, 1)\hspace{0.2cm} \rightarrow\hspace{0.2cm} \underline{x}\hspace{0.05cm}_7 = (1, 1, 1, 1, 1) \hspace{0.05cm}.\]

Zusammen mit dem Vektor $\underline{x} = (u_1, u_2, u_3, p_1, p_2) = (x_1, x_2, x_3, x_4, x_5)$ lauten dann die Prüfbits:

\[p_1 = u_2 \hspace{0.05cm},\hspace{0.2cm}p_2 = u_1 \hspace{0.05cm},\]

und die entsprechenden Prüfgleichungen des Decoders:

\[x_2 + x_4 = 0 \hspace{0.05cm},\hspace{0.2cm}x_1 + x_5 = 0 \hspace{0.05cm}.\]

Man erkennt aus diesen Gleichungen und auch aus obiger Codetabelle:

Dieser Code bietet gegenüber einem Übertragungsfehler hinsichtlich des dritten Bits $(x_3 = u_3)$ keinen Schutz.
Damit ist natürlich weder eine Fehlererkennung und noch weniger Fehlerkorrektur möglich.
Gleiches gilt aber auch für den nichtsystematischen Code entsprechend $\text{Beispiel 7}$ auf der letzten Seite.

Darstellung von SPC und RC als duale Codes

Nun sollen für die bereits im Kapitel Beispiele binärer Blockcodes behandelten Codes noch jeweils die Generatormatrix $\boldsymbol{\rm G}$ und die Prüfmatrix $\boldsymbol{\rm H}$ angegeben werden. Die Codelänge sei für die folgenden Beispiele stets $n = 5$, doch lassen sich die Ergebnisse auch für andere Codelängen in gleicher Weise interpretieren. Es gilt für

den Single–Parity–check Code ⇒ $\text{SPC (5, 4)}$:

\[{ \boldsymbol{\rm H}} = \begin{pmatrix} 1 &1 &1 &1 &1 \end{pmatrix} \hspace{0.05cm},\hspace{0.5cm}{ \boldsymbol{\rm G}} = \begin{pmatrix} 1 &0 &0 &0 &1\\ 0 &1 &0 &0 &1\\ 0 &0 &1 &0 &1\\ 0 &0 &0 &1 &1 \end{pmatrix} \hspace{0.05cm};\]

den Wiederholungscode (Repetition Code) ⇒ $\text{RC (5, 1)}$:

\[{ \boldsymbol{\rm G}} = \begin{pmatrix} 1 &1 &1 &1 &1 \end{pmatrix} \hspace{0.05cm},\hspace{0.5cm}{ \boldsymbol{\rm H}} = \begin{pmatrix} 1 &0 &0 &0 &1\\ 0 &1 &0 &0 &1\\ 0 &0 &1 &0 &1\\ 0 &0 &0 &1 &1 \end{pmatrix} \hspace{0.05cm}.\]

Die jeweils erste Gleichung lässt sich einfach aus der jeweiligen Definition herleiten und die abgeleitete Gleichung folgt aus der Beziehung $\boldsymbol{\rm H} \cdot \boldsymbol{\rm G}^{\rm T} = \boldsymbol{\rm 0}$.

Aus den obigen Matrizen kann verallgemeinert werden:

Die Generatormatrix des $\text{RC (5, 1)}$ ist identisch mit der Prüfmatrix des $\text{SPC (5, 4)}$. Es handelt sich jeweils um $(5 \times 1)$–Matrizen.

Die Prüfmatrix des $\text{RC (5, 1)}$ ist identisch mit der Generatormatrix des $\text{SPC (5, 4)}$. Diese beiden Matrizen haben jeweils $5$ Spalten und $4$ Zeilen.

Dieser Sachverhalt ergibt sich, weil es sich hier um so genannte "duale Codes" handelt. Zur Erklärung benötigen wir noch zwei Definitionen:

$\text{Definition:}$ Zwei lineare Codes $\mathcal{C}$ und $\mathcal{C}\hspace{0.05cm}'$, beide aus ${\rm GF}(2^n)$, sind orthogonal, wenn alle Codeworte $\underline{x} \in \mathcal{C}$ zu allen Codeworten $\underline{x}\hspace{0.05cm}' \in \mathcal{C}\hspace{0.05cm}'$ orthogonal sind. Man bezeichnet dann $\mathcal{C}$ und $\mathcal{C}\hspace{0.05cm}'$ als duale Codes.

$\text{Definition:}$ Zwei Codeworte $\underline{x} \in{\rm GF}(2^n)$ und $\underline{x\hspace{0.05cm}'} \in {\rm GF}(2^n)$ sind immer dann zueinander orthogonal, wenn das innere Produkt verschwindet:

\[\big \langle \underline{x} \cdot \underline{x}\hspace{0.05cm}' \big \rangle = \sum_{i=1 }^{n} x_i \cdot x\hspace{0.05cm}'_i = 0 \hspace{0.05cm}, \hspace{0.5cm} \left \langle \underline{x} \cdot \underline{x}\hspace{0.05cm}' \right \rangle \in {\rm GF}(2^n) \hspace{0.05cm}.\]

Wegen der Produktbildung in ${\rm GF}(2^n)$ sind auch folgende Codewort–Paare zueinander orthogonal:

\[\left \langle \hspace{0.05cm}(0, 1, 1, 0) \hspace{0.05cm}, \hspace{0.5cm} (1, 1, 1, 0) \hspace{0.05cm} \right \rangle = 0\hspace{0.05cm},\hspace{0.2cm} \left \langle \hspace{0.1cm}(0, 1, 1, 0) \hspace{0.05cm}, \hspace{0.2cm} (0, 1, 1, 0) \hspace{0.1cm}\right \rangle = 0\hspace{0.05cm}.\]

Der Code $\mathcal{C}$ spannt einen $k$–dimensionalen Untervektorraum in ${\rm GF}(2^n)$ auf.
Der Untervektorraum des dualen Codes $\mathcal{C}\hspace{0.05cm}'$ ist zu diesem orthogonal und weist die Dimension $n-k$ auf.
Damit gilt: ${\rm dim} \{ \mathcal{C} \} + {\rm dim} \{ \mathcal{C}\hspace{0.05cm}' \} = n\hspace{0.05cm}.$

Einige Eigenschaften des (7, 4, 3)–Hamming–Codes

Fassen wir die bisherigen Ergebnisse dieses Kapitels am Beispiel des systematischen Hamming–Codes nochmals zusammen, der bereits im Kapitel Beispiele binärer Blockcodes ausführlich beschrieben wurde. Dieser $\text{(7, 4, 3)}$–Code ist gekennzeichnet durch

Codeworte des $\text{HC (7, 4, 3)}$

die Anzahl der Prüfgleichungen $m = 3$,
die Codelänge $n = 2^m-1 = 7$,
die Informationswortlänge $k = n-m = 4$,
die Anzahl $2^k =16$ der Codeworte (Dimension),
die Rate $R= k/n = 4/7$,
die minimale Distanz $d_{\rm min} = 3$ $($unabhängig von $m$, $n$ und $k)$.

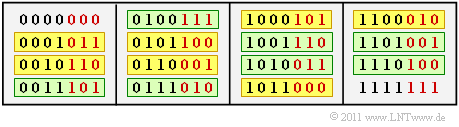
In obiger Tabelle sind die $2^4 = 16$ Codeworte angegeben
(schwarz: vier Informationsbits, rot: drei Prüfbits).

Man erkennt daraus:

Der Code beinhaltet sowohl das Null–Wort $(0000000)$ als auch das Eins–Wort $(1111111)$.
Es gibt sieben Codeworte, die sich aus $(0001011)$ jeweils durch zyklische Verschiebung ergeben (alle gelb hinterlegt).
Es gibt sieben Codeworte, die sich aus $(0011101)$ jeweils durch zyklische Verschiebung ergeben (alle grün hinterlegt).
Zu jedem Codewort existiert auch das "negierte" Codewort, zum Beispiel gibt es neben $(0001011)$ auch das Codewort $(1110100)$.
Die Prüfmatrix kann wie folgt geschrieben werden:

\[{ \boldsymbol{\rm H}} = \begin{pmatrix} 1 &1 &1 &0 &1 &0 &0\\ 0 &1 &1 &1 &0 &1 &0\\ 1 &1 &0 &1 &0 &0 &1 \end{pmatrix}=\left({ \boldsymbol{\rm P}}^{\rm T} \: ; \: { \boldsymbol{\rm I}}_3 \right)\hspace{0.8cm} \Rightarrow\hspace{0.8cm}{ \boldsymbol{\rm P}}^{\rm T} = \begin{pmatrix} 1 &1 &1 &0 \\ 0 &1 &1 &1 \\ 1 &1 &0 &1 \end{pmatrix}\hspace{0.05cm},\hspace{0.2cm}{ \boldsymbol{\rm I}}_3 = \begin{pmatrix} 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \end{pmatrix}\hspace{0.05cm}.\]

Dementsprechend gilt für die Generatormatrix:

\[{ \boldsymbol{\rm G}} =\left({ \boldsymbol{\rm I}}_4 \: ; \: { \boldsymbol{\rm P}}\right) = \begin{pmatrix} 1 &0 &0 &0 &1 &0 &1\\ 0 &1 &0 &0 &1 &1 &1\\ 0 &0 &1 &0 &1 &1 &0\\ 0 &0 &0 &1 &0 &1 &1 \end{pmatrix}\hspace{0.05cm}.\]