Exercise 4.08: Decision Regions at Three Symbols

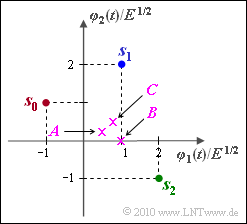
Signal space constellations with $M = 3$ symbols

We consider a signal space constellation in two-dimensional space $(N = 2)$ with the signal set:

$$\boldsymbol{ s }_0 = (-1, 1)\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ s }_1 = (1, 2)\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ s }_2 = (2, -1)\hspace{0.05cm},$$

in each case referred to the normalization value $\sqrt {E}$.

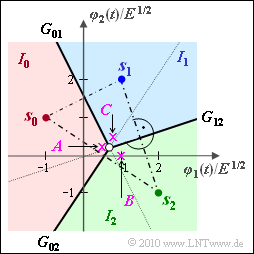
The decision regions $I_0$, $I_1$ and $I_2$ are sought, with the following considerations:

The region $I_i$ should contain the signal space point $\boldsymbol{s}_i$ ($i = 0, 1, 2$).
The signals $\boldsymbol{s}_0$, $\boldsymbol{s}_1$ and $\boldsymbol{s}_2$ are equally probable.
The regions are to be determined in such a way that the smallest error probability results for the AWGN channel.

With these preconditions, the decision boundaries $G_{\it ik}$ between regions $I_i$ and $I_k$ are respectively straight lines exactly midway between $\boldsymbol{s}_i$ and $\boldsymbol{s}_k$ $(i = 0, 1, 2; \ \ k = 0, 1, 2; \ \ i ≠ k)$.

With crosses in the above graph are three received values

$$\boldsymbol{ A } = (0.50, \hspace{0.1cm}0.25)\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ B } = (1, \hspace{0.1cm}0)\hspace{0.05cm}, \hspace{0.2cm} \boldsymbol{ C } = (0.75, \hspace{0.1cm}0.50)$$

each of which is to be assigned to a region $I_i$ in subtask (5).

Notes:

The exercise belongs to the chapter "Approximation of the Error Probability".

To simplify the notation, the following is used:

$$x = {\varphi_1(t)}/{\sqrt{E}}\hspace{0.05cm}, \hspace{0.2cm} y = {\varphi_2(t)}/{\sqrt{E}}\hspace{0.05cm}.$$

Questions

Solution

Decision regions

(1) Solution 1 is correct:

The connecting line between the signal points $\boldsymbol{s}_0 = (–1, 1)$ and $\boldsymbol{s}_1 = (1, 2)$ has the gradient $1/2$ (see diagram).
The decision boundary intersects the connecting line at $(\boldsymbol{s}_0 + \boldsymbol{s}_1)/2 = (0, 1.5)$ and has the slope $2$ (rotation of the connecting line by $90^\circ$).
From this follows: $y = 1.5 - 2 x \hspace{0.05cm}.$

(2) Solution 3 is correct:

The connecting line between $\boldsymbol{s}_0 = (–1, 1)$ and $\boldsymbol{s}_2 = (2, 1)$ has the slope $–2/3$ and intersects the decider boundary $G_{\rm 02}$ (with the slope $3/2$) at $(0.5, 0)$.
From this follows: $y = {3}/{2} \left ( x - {1}/{2} \right ) = -{3}/{4} + {3}/{2} \cdot x\hspace{0.05cm}.$

(3) Here solution 2 is applicable:

The line connecting $\boldsymbol{s}_1 = (1, 2)$ and $\boldsymbol{s}_2 = (2, \, –1)$ intersects the decision boundary $G_{\rm 12}$ at $(1.5, 0.5)$ and has slope $–3$.
Consequently, the slope of $G_{\rm 12} = 1/3$ and the equation of the decision boundary $G_{\rm 12}$ is:

$$y - {1}/{2} = {1}/{3} \cdot \left ( x - {3}/{2} \right ) = {x}/{3} - {1}/{2}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}y = {x}/{3} \hspace{0.05cm}.$$

(4) The graph already shows that the correct answer is YES.

The intersection of $G_{\rm 01}$ and $G_{\rm 12}$ (white circle) is at $(9/14, 3/14)$, because of

$${3}/{2} - 2 x = {x}/{3} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} {3}/{2} = {7}/{3} \cdot x \hspace{0.3cm} \Rightarrow \hspace{0.3cm} y = {3}/{14} \hspace{0.05cm}.$$

The straight line $G_{\rm 02}$ also passes through this point:

$$y(x = {9}/{14}) =-{3}/{4} + {3}/{2} \cdot x = -{3}/{4} + {3}/{2} \cdot {9}/{14} =\frac{-21+27}{28}= {3}/{14} \hspace{0.05cm}.$$

(5) According to the graph all statements mentioned are correct.

	$y = 3/2 \, -2 \cdot x$,
	$y = x/3$,
	$y = \, -3/4 + 3/2 \cdot x$.

	$\boldsymbol{A} = (0.5, 0.25)$ belongs to region $I_0$.
	$\boldsymbol{B} = (1, 0)$ belongs to region $I_2$.
	$\boldsymbol{C} = (0.75, 0.5)$ belongs to region $I_1$.

	Yes.
	No.