Exercise 1.1: ISDN Supply Lines

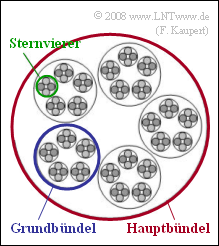
Main bundle, basic bundle, and star quad

In ISDN (Integrated Services Digital Network) the final branch (near the subscriber) is connected to a local exchange (OVSt) by a copper twisted pair, whereby two twisted pairs are twisted into a so-called star quad. Several such star quads are then combined to form a basic bundle, and several basic bundles are combined to form a main bundle (see graphic).

In the network of Deutsche Telekom (formerly: Deutsche Bundespost), mostly copper lines with 0.4 mm core diameter are found, for whose attenuation and phase function the following equations are given in [PW95]:

$$\frac{a_{\rm K}(f)}{\rm dB} = \left [ 5.1 + 14.3 \cdot \left (\frac{f}{\rm MHz}\right )^{0.59}\right ]\cdot\frac{l}{\rm km} \hspace{0.05cm},$$

$$\frac{b_{\rm K}(f)}{\rm rad} = \left [ 32.9 \cdot \frac{f}{\rm MHz} + 2.26 \cdot \left (\frac{f}{\rm MHz}\right )^{0.5}\right ]\cdot\frac{l}{\rm km} \hspace{0.05cm}.$$

Here $l$ denotes the line length.

Notes:

The exercise belongs to the chapter "General Description of ISDN".
In particular, reference is made to the section "Network infrastructure for ISDN".
Further information on the attenuation of copper lines can be found in the chapter "Properties of Electrical Cables" of the book "Linear and Time Invariant Systems".
[PW95] refers to the following publication: Pollakowski, P.; Wellhausen, H.-W.: Eigenschaften symmetrischer Ortsanschlusskabel im Frequenzbereich bis 30 MHz. Deutsche Telekom AG, Forschungs- und Technologiezentrum Darmstadt, 1995.

Questions

$N \ = \ $

	The two transmission directions interfere with each other.
	Crosstalk noise may occur.
	Intersymbol interference occurs.

$l \ = \ $

$\ \rm km$

$a_{\rm K}(f = 120 \ \rm kHz) \ = \ $

$\ \rm dB$

$b_{\rm K}(f = 120 \ \rm kHz) \ = \ $

$\ \rm rad$

Solution

(1) Two-wire transmission is used in the connection area. The possible connections are equal to the number of pairs in the main cable: $\underline{N = 50}$.

(2) Solutions 1 and 2 are correct:

Two-wire transmission requires a directional separation method, namely the so-called fork circuit. This has the task that at receiver $\rm A$ only the transmitted signal of subscriber $\rm B$ arrives, but not the own transmitted signal. This is generally quite successful with narrowband signals – for example, speech – but not completely.
Due to inductive and capacitive couplings, crosstalk can occur from the twin wire located in the same star quad, whereby near-end crosstalk (i.e. the interfering transmitter and the interfered receiver are located together) leads to greater impairments than far-end crosstalk.
On the other hand, the last solution is not applicable. Intersymbol interference – i.e. the mutual interference of neighboring symbols – can certainly occur, but it is not related to two-wire transmission. The reason for this are rather (linear) distortions due to the specific attenuation and phase curves.

(3) The DC signal attenuation by a factor of $4$ can be expressed as follows:

$$a_{\rm K}(f = 0) = 20 \cdot {\rm lg}\,\,(4) = 12.04\,{\rm dB}\hspace{0.05cm}.$$

With the given coefficient $\text{5.1 dB/km}$, this gives the line length $l = 12.04/5.1\hspace{0.15cm}\underline{ = 2.36 \ \rm km}$.

(4) Using the given equations and $ l = 2.36 \ \rm km$, we obtain:

$$a_{\rm K}(f = 120\,{\rm kHz})= (5.1 + 14.3 \cdot 0.12^{\hspace{0.05cm}0.59}) \cdot 2.36\,{\rm dB} \hspace{0.15cm}\underline{\approx 21.7\,{\rm dB}}\hspace{0.05cm},$$

$$b_{\rm K}(f = 120\,{\rm kHz}) = (32.9 \cdot 0.12 + 2.26 \cdot 0.12^{\hspace{0.05cm}0.5}) \cdot 2.36\,{\rm rad}\hspace{0.15cm}\underline{ \approx 11.2\,{\rm rad}}\hspace{0.05cm}.$$