Exercise 2.15Z: Block Error Probability once more

• Return to book

Binominal probabilities

Using a Reed–Solomon code with the correctability  $t$  and  "Bounded Distance Decoding"  $\rm$  $\rm (BDD)$  is obtained with

• the code word length  $n$  and

• the symbol falsification probability  $\varepsilon_{\rm S}$

for the block error probability:

$${\rm Pr(block\:error)} = \sum_{f = t + 1}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} \hspace{0.05cm}.$$

In this exercise,  the block error probability for the  $\rm RSC \, (7, \, 3, \, 5)_8$  and various  $\varepsilon_{\rm S}$  values shall be calculated and approximated.

• The above equation is reminiscent of the  "Biomial Distribution". 

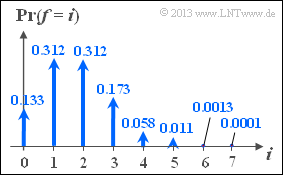
• The graph shows the probabilities of the binomial distribution for parameters  $n = 7$  ("code word length") and  $\varepsilon_{\rm S} = 0.25$  ("symbol falsification probability").

Hints:

• This exercise belongs to the chapter  "Error Probability and Application Areas".

• For checking,  you can use the interactive HTML5/JavaScript applet  "Binomial and Poisson Distribution".

Questions

1

What is the block error probability for  $\varepsilon_{\rm S} = 10^{-1}$?

$\rm Pr(block\:error) \ = \ $ $\ \cdot 10^{-2}$

2

What is the block error probability for  $\varepsilon_{\rm S} =10^{-2}$?

$\rm Pr(block\:error) \ = \ $ $\ \cdot 10^{-5}$

3

What result is obtained for  $\varepsilon_{\rm S} =10^{-2}$,  considering only the term  $f = t + 1$ ?

$\rm Approximation \text{:} \hspace{0.2cm} Pr(block\:error) \ \approx \ $ $\ \cdot 10^{-5}$

4

What result is obtained approximately for  $\varepsilon_{\rm S} = 10^{-3}$?

$\rm Pr(block\:error) \ \approx \ $ $\ \cdot 10^{-8}$

5

What  $\varepsilon_{\rm S}$  is needed for the block error probability  $10^{-10}$?

$\varepsilon_{\rm S} \ = \ $ $\ \cdot 10^{-4}$

Solution

Solution

(1)  For the  $\rm RSC \, (7, \, 3, \, 5)_8$,  because  $d_{\rm min} = 5 \ \Rightarrow \ t = 2$  gives the block error probability:

$${\rm Pr(block\:error)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \sum_{f = 3}^{7} {7 \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{7-f}$$

$$\Rightarrow \hspace{0.3cm}{\rm Pr(block\:error)} ={7 \choose 3} \cdot 0.1^3 \cdot 0.9^4 + {7 \choose 4} \cdot 0.1^4 \cdot 0.9^3 + {7 \choose 5} \cdot 0.1^5 \cdot 0.9^2+ {7 \choose 6} \cdot 0.1^6 \cdot 0.9+ {7 \choose 7} \cdot 0.1^7 \hspace{0.05cm}.$$

• According to this calculation,  five terms would have to be considered.  However,  since

$${\rm Pr(block\:error)} = \sum_{f = 0}^{n} {n \choose f} \cdot {\varepsilon_{\rm S}}^f \cdot (1 - \varepsilon_{\rm S})^{n-f} = 1$$

is also valid,  the following calculation is faster:

$${\rm Pr(block\:error)} =1 - \big [ {7 \choose 0} \cdot 0.9^7 + {7 \choose 1} \cdot 0.1 \cdot 0.9^6 + {7 \choose 2} \cdot 0.1^2 \cdot 0.9^5 \big ] =1 - \big [ 0.4783 + 0.3720 + 0.1240 \big ] \hspace{0.15cm} \underline{= 2.57 \cdot 10^{-2}} \hspace{0.05cm}.$$

(2)  Analogous to the subtask  (1)  one obtains here:

$${\rm Pr(block\:error)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} 1 - \big [ 0.99^7 + 7 \cdot 0.01 \cdot 0.99^6 + 21 \cdot 0.01^2 \cdot 0.99^5 \big ] =1 - \big [ 0.9321 + 0.0659 + 0.0020 \big ] \approx 0 \hspace{0.05cm}.$$

• This means:   For the probability  $\varepsilon_{\rm S} = 0.01$  the simplified calculation is very error-prone,  because a value close to  $1$  results for the bracket expression.

• The full calculation yields here:

$${\rm Pr(block\:error)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {7 \choose 3} \cdot 0.01^3 \cdot 0.99^4 + {7 \choose 4} \cdot 0.01^4 \cdot 0.99^3 + {7 \choose 5} \cdot 0.01^5 \cdot 0.99^2+ {7 \choose 6} \cdot 0.01^6 \cdot 0.99+ {7 \choose 7} \cdot 0.01^7$$

$$\Rightarrow \hspace{0.3cm}{\rm Pr(block\:error)}= 10^{-6} \cdot \big [ 33.6209 + 0.3396 + 0.0021 + ... \big ] \hspace{0.15cm} \underline{ \approx 3.396 \cdot 10^{-5}} \hspace{0.05cm}.$$

(3)  From the sample solution to the subtask  (2)  the result can be read directly:

$${\rm Pr(block\:error)} \hspace{0.15cm} \underline{ \approx 3.362 \cdot 10^{-5}} \hspace{0.05cm}.$$

• The relative error is about  $-1\%$.

• The minus sign indicates that this is only an approximation and not a bound:  The approximate value is slightly smaller than the actual value.

(4)  Restricting to the relevant term  $(f = 3)$,  we get  $\varepsilon_{\rm S} = 0.001$:

$${\rm Pr(block\:error)} \approx {7 \choose 3} \cdot [10^{-3}]^3 \cdot 0.999^4 \hspace{0.15cm} \underline{ \approx 3.49 \cdot 10^{-8}} \hspace{0.05cm}.$$

• The relative error here is only about  $-0.1\%$.

(5)  According to the derived approximation,  the following holds for the considered code:

$${\rm Pr(block\:error)} \approx {7 \choose 3} \cdot {\varepsilon_{\rm S}}^3 = 35 \cdot {\varepsilon_{\rm S}}^3\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Pr(block\:error)} = 10^{-10}: \hspace{0.4cm} {\varepsilon_{\rm S}} = \big ( \frac{10^{-10}}{35} \big )^{1/3} = 2.857^{1/3} \cdot 10^{-4} \hspace{0.15cm} \underline{ \approx 1.42 \cdot 10^{-4}}\hspace{0.05cm}.$$