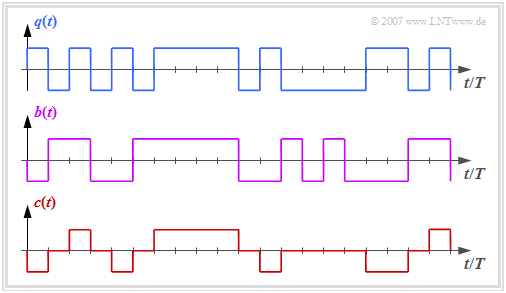
Principle of Pseudo-Ternary Coding

Open Applet in new Tab   Deutsche Version Öffnen

Applet Description

Das Applet behandelt die Eigenschaften der bekanntesten Pseudoternärcodes, nämlich:

1.   Bipolarcode erster Ordnung bzw.  $\rm AMI$–Code  (von: Alternate Mark Inversion),  gekennzeichnet durch die Parameter  $N_{\rm C} = 1, \ K_{\rm C} = +1$,
2.   Duobinärcode,  $(\rm DUOB)$,  Codeparameter:  $N_{\rm C} = 1, \ K_{\rm C} = -1$,
3.   Bipolarcode zweiter Ordnung  $(\rm BIP2)$,  Codeparameter:  $N_{\rm C} = 2, \ K_{\rm C} = +1$.

Am Eingang liegt die redundanzfreie binäre bipolare Quellensymbolfolge  $\langle \hspace{0.05cm}q_\nu \hspace{0.05cm}\rangle \ \in \{+1, -1\}$   ⇒   Rechtecksignal  $q(t)$  an.  Verdeutlicht wird die Generierung

• der binär–vorcodierten Folge  $\langle \hspace{0.05cm}b_\nu \hspace{0.05cm}\rangle \ \in \{+1, -1\}$,  dargestellt durch das ebenfalls redundanzfreie binäre bipolare Rechtecksignal  $b(t)$,
• der pseudoternären Codefolge  $\langle \hspace{0.05cm}c_\nu \hspace{0.05cm}\rangle \ \in \{+1,\ 0, -1\}$,  dargestellt durch das redundante ternäre bipolare Rechtecksignal  $c(t)$,
• das gleichermaßen redundante ternäre Sendesignal  $s(t)$, gekennzeichnet durch die Amplitudenkoeffizienten  $a_\nu $,  und den (Sende–) Grundimpuls  $g(t)$:

$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g( t - \nu \cdot T)\hspace{0.05cm}.$$

Der Grundimpuls  $g(t)$  –  im Applet  "Rechteck",  "Nyquist" und  "Wurzel–Nyquist"  –  bestimmt nicht nur die Form des Sendesignals, sondern auch den Verlauf

• der Autokorrelationsfunktion  $\rm (AKF)$  $\varphi_s (\tau)$  und
• des zugehörigen Leistungsdichtespektrums  $\rm (LDS)$  ${\it \Phi}_s (f)$.

Das Applet zeigt auch, dass das gesamte Leistungsdichtespektrum  ${\it \Phi}_s (f)$ aufgeteilt werden kann in den Anteil  ${\it \Phi}_a (f)$, der die statistischen Bindungen der Amplitudenkoeffizienten  $a_\nu$   berücksichtigt, und das Energiedichtespektrum $ {\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f) = |G(f)|^2 $, gekennzeichnet durch die Impulsform  $g(t)$.

Anmerkung:   Im Applet wird kein Unterschied zwischen den Codersymbolen  $c_\nu \in \{+1,\ 0, -1\}$  und den Amplitudenkoeffizienten  $a_\nu \in \{+1,\ 0, -1\}$  gemacht.  Dabei sollte nicht vergessen werden, dass die  $a_\nu$  stets Zahlenwerte sind, während für die Codersymbole auch die Notation  $c_\nu \in \{\text{Plus},\ \text{Null},\ \text{Minus}\}$  zulässig wäre.

General description of the pseudo-multilevel codes

In symbolwise coding,  each incoming source symbol  $q_\nu$  generates an encoder symbol  $c_\nu$,  which depends not only on the current input symbol  $q_\nu$  but also on the  $N_{\rm C}$  preceding symbols  $q_{\nu-1}$, ... , $q_{\nu-N_{\rm C}} $.   $N_{\rm C}$  is referred to as the  "order"  of the code.

Typical for symbolwise coding is that

• the symbol duration  $T$  of the encoded signal  (and of the transmitted signal)  matches the bit duration  $T_{\rm B}$  of the binary source signal,  and

• encoding and decoding do not lead to major time delays,  which are unavoidable when block codes are used.
  
  

The  "pseudo-multilevel codes"  – better known as  "partial response codes"  –  are of special importance.  In the following,  only  "pseudo-ternary codes"   ⇒   level number  $M = 3$  are considered. 

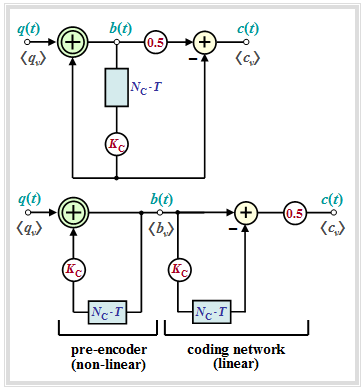
• These can be described by the block diagram corresponding to the left graph. 
• In the right graph an equivalent circuit is given,  which is very suitable for an analysis of these codes.

Block diagram  (above)  and equivalent circuit  (below)  of a pseudo-ternary encoder

One can see from the two representations:

• The pseudo-ternary encoder can be split into the  "non-linear pre-encoder"  and the  "linear coding network",  if the delay by  $N_{\rm C} \cdot T$  and the weighting by  $K_{\rm C}$  are drawn twice for clarity  – as shown in the right equivalent figure.

• The  "non-linear pre-encoder"  obtains the precoded symbols  $b_\nu$,  which are also binary,  by a modulo–2 addition  ("antivalence")  between the symbols  $q_\nu$  and  $K_{\rm C} \cdot b_{\nu-N_{\rm C}} $: 

$$q_\nu \in \{-1, +1\},\hspace{0.1cm} K_{\rm C} \in \{-1, +1\}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}b_\nu \in \{-1, +1\}\hspace{0.05cm}.$$

• Like the source symbols  $q_\nu$,  the symbols  $b_\nu$  are statistically independent of each other.  Thus,  the pre-encoder does not add any redundancy.  However,  it allows a simpler realization of the decoder and prevents error propagation after a transmission error.
  

• The actual encoding from binary  $(M_q = 2)$  to ternary  $(M = M_c = 3)$  is done by the  "linear coding network"  by the conventional subtraction

$$c(t) ={1}/{2} \cdot \big [b(t) - K_{\rm C} \cdot b(t- N_{\rm C}\cdot T)\big] \in \{-1, \ 0, +1\}\hspace{0.05cm},$$

which can be described by the following  "impulse response"  resp.  "transfer function"  with respect to the input signal  $b(t)$  and the output signal  $c(t)$: 

$$h_{\rm C}(t) = {1}/{2} \cdot \big [\delta(t) - K_{\rm C} \cdot \delta(t- N_{\rm C}\cdot T)\big] \ \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ H_{\rm C}(f) ={1}/{2} \cdot \left [1 - K_{\rm C} \cdot {\rm e}^{- {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}N_{\rm C}\hspace{0.05cm}\cdot \hspace{0.05cm}T}\right]\hspace{0.05cm}. $$

• The relative redundancy is the same for all pseudo-ternary codes.  Substituting  $M_q=2$,  $M_c=3$  and  $T_c =T_q$  into the  "general definition equation",  we obtain

$$r_c = 1- \frac{R_q}{R_c} = 1- \frac{T_c}{T_q} \cdot \frac{{\rm log_2}\hspace{0.05cm} (M_q)}{{\rm log_2} \hspace{0.05cm}(M_c)} = 1- \frac{T_c}{T_q \cdot {\rm log_2} \hspace{0.05cm}(M_c)}\hspace{0.5cm}\Rightarrow \hspace{0.5cm} r_c = 1 -1/\log_2\hspace{0.05cm}(3) \approx 36.9 \%\hspace{0.05cm}.$$

The  $\text{transmitted signal of all pseudo-ternary codes}$  is always represented as follows:

$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g( t - \nu \cdot T)\hspace{0.05cm}.$$

• The property of the current pseudo-ternary code is reflected in the statistical bonds between the  $a_\nu$  In all cases  $a_\nu \in \{-1, \ 0, +1\}$.
• The basic transmitting pulse  $g(t)$  provides on the one hand the required energy, but has also influence on the statistical bonds within the signal.
• In addition to the NRZ rectangular pulse  $g_{\rm R}(t)$ can be selected in the program: 

• the Nyquist impulse   ⇒   impulse response of the raised cosine low-pass with rolloff factor $r$:

$$g_{\rm Nyq}(t)={\rm const.} \cdot \frac{\cos(\pi \cdot r\cdot t/T)}{1-(2\cdot r\cdot t/T)^2} \cdot {\rm si}(\pi \cdot t/T) \ \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ G_{\rm Nyq}(f),$$

• the root Nyquist impulse   ⇒   impulse response of the root raised cosine lowpass with rolloff factor $r$:

$$g_{\sqrt{\rm Nyq} }(t)\ \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\ \ \ G_{\sqrt{\rm Nyq} }(f)={\rm const.} \cdot \sqrt{G_{\rm Nyq}(f)} .$$

Eigenschaften des AMI-Codes

Die Pseudoternärcodes unterscheiden sich in den Parametern  $N_{\rm C}$  und  $K_{\rm C}$.  Der bekannteste Vertreter ist der  Bipolarcode erster Ordnung  mit den Codeparametern  $N_{\rm C} = 1$  und  $K_{\rm C} = 1$, der auch unter der Bezeichnung  AMI–Code  (von: Alternate Mark Inversion) bekannt ist.

AMI– und HDB3–Codierung, jeweils dargestellt mit Rechtecksignalen

Dieser wird zum Beispiel bei  ISDN  (Integrated Services Digital Networks) auf der so genannten  $S_0$–Schnittstelle eingesetzt.

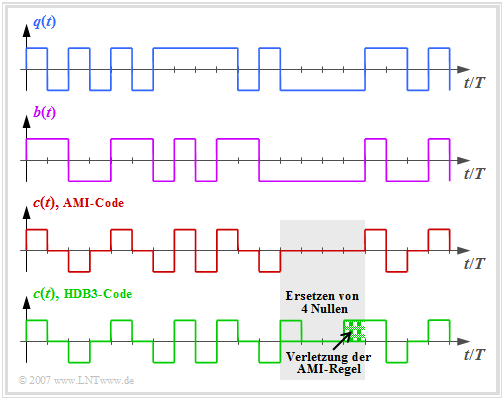
Die Grafik zeigt oben das binäre Quellensignal  $q(t)$. Im zweiten und dritten Diagramm sind dargestellt:

• das ebenfalls binäre Signal  $b(t)$  nach dem Vorcodierer, und
• das Codersignal  $c(t) = s(t)$  des AMI–Codes.

Man erkennt das einfache AMI–Codierprinzip:

• Jeder Binärwert "-1" von  $q(t)$   ⇒   Symbol  $\rm L$  wird durch den ternären Koeffizienten  $a_\nu = 0$  codiert.
  
• Der Binärwert "+1" von  $q(t)$   ⇒   Symbol  $\rm H$  wird alternierend mit  $a_\nu = +1$  und  $a_\nu = -1$  dargestellt.
  
  

Damit wird sichergestellt, dass im AMI–codierten Signal keine langen "+1"– und auch keine keine langen "–1"–Sequenzen enthalten sind, was bei einem gleichsignalfreien Kanal zu Problemen führen würde.

Dagegen ist das Auftreten langer Nullfolgen durchaus möglich, bei denen über einen längeren Zeitraum keine Taktinformation übertragen wird.

Um dieses zweite Problem zu vermeiden, wurden einige modifizierte AMI–Codes entwickelt, zum Beispiel der B6ZS–Code  und der HDB3–Code:

• Beim HDB3–Code  (grüne Kurve in obiger Grafik) werden vier aufeinanderfolgende Nullen im AMI–codierten Signal durch eine Teilsequenz ersetzt, die die AMI–Codierregel verletzt.
  

• Im grau hinterlegten Bereich ist dies die Folge "+ 0 0 +", da das letzte Symbol vor der Ersetzung ein "Minus" war.
  

• Damit ist beim HDB3–Code die Anzahl aufeinanderfolgender Nullen auf  $3$  begrenzt und beim  B6ZS–Code  auf  $5$.
• Der Decoder erkennt diese Codeverletzung und ersetzt "+ 0 0 +" wieder durch "0 0 0 0".
  

Zur AKF–Berechnung eines Digitalsignals

In der Versuchsdurchführung werden einige Größen und Zusamenhänge verwendet, die hier kurz eräutert werden sollen:

•   Das (zeitlich unbegrenzte) Digitalsignal beinhaltet sowohl die Quellenstatistik $($Amplitudenkoeffizienten  $a_\nu$)  als auch die Sendeimpulsform  $g(t)$:

$$s(t) = \sum_{\nu = -\infty}^{+\infty} a_\nu \cdot g ( t - \nu \cdot T)\hspace{0.05cm}.$$

•   Ist  $s(t)$  die Musterfunktion eines stationären und ergodischen Zufallsprozesses, so gilt für die  Autokorrelationsfunktion  $\rm (AKF)$:

$$\varphi_s(\tau) = {\rm E}\big [s(t) \cdot s(t + \tau)\big ] = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot\varphi^{^{\bullet} }_{gs}(\tau - \lambda \cdot T)\hspace{0.05cm}.$$

•   Diese Gleichung beschreibt die Faltung der diskreten AKF  $\varphi_a(\lambda) = {\rm E}\big [ a_\nu \cdot a_{\nu + \lambda}\big]$  der Amplitudenkoeffizienten mit der Energie–AKF des Grundimpulses:

$$\varphi^{^{\bullet} }_{g}(\tau) = \int_{-\infty}^{+\infty} g ( t ) \cdot g ( t + \tau)\,{\rm d} t \hspace{0.05cm}.$$

• Der Punkt soll darauf hinweisen, dass  $\varphi^{^{\bullet} }_{g}(\tau)$  die Einheit einer Energie besitzt, während  $\varphi_s(\tau)$  eine Leistung angibt und  $\varphi_a(\lambda)$  dimensionslos ist.

Zur LDS-Berechnung eines Digitalsignals

Die Entsprechungsgröße zur AKF ist im Frequenzbereich das Leistungsdichtespektrum  $\rm (LDS)$  ${\it \Phi}_s(f)$, das mit  $\varphi_s(\tau)$  über das Fourierintegral fest verknüpft ist:

$$\varphi_s(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} {\it \Phi}_s(f) = \int_{-\infty}^{+\infty} \varphi_s(\tau) \cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \tau} \,{\rm d} \tau \hspace{0.05cm}.$$

• Das Leistungsdichtespektrum  ${\it \Phi}_s(f)$  kann unter Berücksichtigung der Dimensionsbereinigung  $(1/T)$  als Produkt zweier Funktionen dargestellt werden:

$${\it \Phi}_s(f) = {\it \Phi}_a(f) \cdot {1}/{T} \cdot |G_s(f)|^2 \hspace{0.05cm}.$$

• Der erste Term  ${\it \Phi}_a(f)$  ist dimensionslos und beschreibt die spektrale Formung des Sendesignals durch die statistischen Bindungen der Quelle:
  

$$\varphi_a(\lambda) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm}{\it \Phi}_a(f) = \sum_{\lambda = -\infty}^{+\infty}\varphi_a(\lambda)\cdot {\rm e}^{- {\rm j}\hspace{0.05cm} 2 \pi f \hspace{0.02cm} \lambda \hspace{0.02cm}T} = \varphi_a(0) + 2 \cdot \sum_{\lambda = 1}^{\infty}\varphi_a(\lambda)\cdot\cos ( 2 \pi f \lambda T) \hspace{0.05cm}.$$

• ${\it \Phi^{^{\hspace{0.08cm}\bullet}}_{g}}(f)$  berücksichtigt die spektrale Formung durch  $g(t)$. Je schmaler dieser ist, desto breiter ist  $\vert G(f) \vert^2$  und um so größer ist damit der Bandbreitenbedarf:

$$\varphi^{^{\hspace{0.05cm}\bullet}}_{g}(\tau) \hspace{0.4cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet \hspace{0.4cm} {\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f) = |G(f)|^2 \hspace{0.05cm}.$$

• Das Energiedichtespektrum ${\it \Phi^{^{\hspace{0.08cm}\bullet}}_{g}}(f)$  hat die Einheit  $\rm Ws/Hz$  und das Leistungsdichtespektrum  ${\it \Phi_{s}}(f)$  nach der Division durch den Symbolabstand  $T$  die Einheit  $\rm W/Hz$.

Leistungsdichtespektrum des AMI-Codes

Der Frequenzgang des linearen Codiernetzwerks eines Pseudoternärcodes lautet allgemein:

$$H_{\rm C}(f) = {1}/{2} \cdot \big [1 - K_{\rm C} \cdot {\rm e}^{-{\rm j}\hspace{0.03cm}\cdot \hspace{0.03cm} 2\pi\hspace{0.03cm}\cdot \hspace{0.03cm}f \hspace{0.03cm}\cdot \hspace{0.03cm} N_{\rm C}\hspace{0.03cm}\cdot \hspace{0.03cm}T} \big] ={1}/{2} \cdot \big [1 - K \cdot {\rm e}^{-{\rm j}\hspace{0.03cm}\cdot \hspace{0.03cm} \alpha} \big ]\hspace{0.05cm}.$$

Damit ergibt sich für das Leistungsdichtespektrum (LDS) der Amplitudenkoeffizienten  $(K$  und  $\alpha$  sind Abkürzungen entsprechend obiger Gleichung$)$:

$$ {\it \Phi}_a(f) = | H_{\rm C}(f)|^2 = \frac{\big [1 - K \cos (\alpha) + {\rm j}\cdot K \sin (\alpha) \big ] \big [1 - K \cos (\alpha) - {\rm j}\cdot K \sin (\alpha) \big ] }{4} = \text{...} = {1}/{4} \cdot \big [2 - 2 \cdot K \cdot \cos (\alpha) \big ] $$

Leistungsdichtespektrum des AMI-Codes

$$ \Rightarrow \hspace{0.3cm}{\it \Phi}_a(f) = | H_{\rm C}(f)|^2 = {1}/{2} \cdot \big [1 - K_{\rm C} \cdot \cos (2\pi f N_{\rm C} T)\big ] \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm} \varphi_a(\lambda \cdot T)\hspace{0.05cm}.$$

Insbesondere erhält man für das Leistungsdichtespektrum (LDS) des AMI–Codes $(N_{\rm C} = K_{\rm C} = 1)$:

$${\it \Phi}_a(f) = {1}/{2} \cdot \big [1 - \cos (2\pi f T)\big ] = \sin^2 (\pi f T)\hspace{0.05cm}.$$

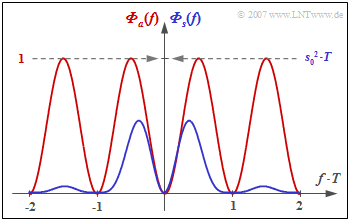
Die Grafik zeigt

• das LDS  ${\it \Phi}_a(f)$  der Amplitudenkoeffizienten (rote Kurve), und
  
• das LDS  ${\it \Phi}_s(f)$  des gesamten Sendesignals (blau), gültig für NRZ–Rechteckimpulse.
  

Man erkennt aus dieser Darstellung

• die Gleichsignalfreiheit des AMI–Codes, da  ${\it \Phi}_a(f = 0) = {\it \Phi}_s(f = 0) = 0$  ist,
  
• die Leistung  $P_{\rm S} = s_0^2/2$  des AMI–codierten Sendesignals (Integral über  ${\it \Phi}_s(f)$  von  $- \infty$  bis  $+\infty$).

Hinweise:

• Das LDS von HDB3– und B6ZS–Code weicht von dem des AMI–Codes nur unwesentlich ab.
  
• Die hier behandelte Thematik können Sie sich mit dem interaktiven Applet  Signale, AKF und LDS der Pseudoternärcodes  verdeutlichen.

Eigenschaften des Duobinärcodes

Leistungsdichtespektrum des Duobinärcodes

Der Duobinärcode ist durch die Codeparameter  $N_{\rm C} = 1$  und  $K_{\rm C} = -1$  festgelegt. Damit ergibt sich für das Leistungsdichtespektrum (LDS) der Amplitudenkoeffizienten bzw. für das LDS des Sendesignals:

$${\it \Phi}_a(f) ={1}/{2} \cdot \big [1 + \cos (2\pi f T)\big ] = \cos^2 (\pi f T)\hspace{0.05cm},$$

$$ {\it \Phi}_s(f) = s_0^2 \cdot T \cdot \cos^2 (\pi f T)\cdot {\rm si}^2 (\pi f T)= s_0^2 \cdot T \cdot {\rm si}^2 (2 \pi f T) \hspace{0.05cm}.$$

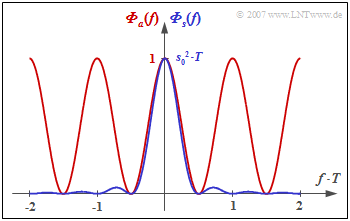
Die Grafik zeigt das Leistungsdichtespektrum

• der Amplitudenkoeffizienten   ⇒   ${\it \Phi}_a(f)$  als rote Kurve,
  
• des gesamten Sendsignals   ⇒   ${\it \Phi}_s(f)$  als blaue Kurve.
  
  

In der zweiten Grafik sind die Signale  $q(t)$,  $b(t)$  und  $c(t) = s(t)$  skizziert. Wir verweisen hier wieder auf das Applet  Signale, AKF und LDS der Pseudoternärcodes, das auch die Eigenschaften des Duobinärcodes verdeutlicht.

Signale bei Duobinärcodierung

Aus diesen Darstellungen geht hervor:

• Beim Duobinärcode können beliebig viele Symbole mit gleicher Polarität ("+1" bzw. "–1") direkt aufeinanderfolgen.
• Deshalb gilt  ${\it \Phi}_a(f = 0)=1$  und  ${\it \Phi}_s(f = 0) = 1/2 \cdot s_0^2 \cdot T$.
  
• Dagegen tritt beim Duobinärcode die alternierende Folge " ... , +1, –1, +1, –1, +1, ... " nicht auf, die hinsichtlich Impulsinterferenzen besonders störend ist.
• Deshalb gilt beim Duobinärcode:  ${\it \Phi}_s(f = 1/(2T) = 0$.
  
• Das Leistungsdichtespektrum  ${\it \Phi}_s(f)$  des pseudoternären Duobinärcodes ist identisch mit dem LDS bei redundanzfreier Binärcodierung mit halber Rate $($Symboldauer  $2T)$.
  

Exercises

• First, select the number  $(1,\ 2, \text{...} \ )$  of the task to be processed.  The number  "$0$"  corresponds to a "Reset":  Same setting as at program start.
• A task description is displayed.  The parameter values are adjusted.  Solution after pressing "Show Solution".

(1)  Consider and interpret the binary pre–coding of the  $\text{AMI}$  code using the source symbol sequence  $\rm C$  assuming  $b_0 = +1$.

• The modulo–2 addition can also be taken as "antivalence".  It holds  $b_{\nu} = +1$,  if  $q_{\nu}$  and  $b_{\nu - 1}$  differ, otherwise set  $b_{\nu} = -1$ :

  $b_1 = (q_1 = +1)\ {\rm XOR}\ (b_0= +1) = -1,\ \ b_2 = (q_2 = -1)\ {\rm XOR}\ (b_1= -1) = -1,\ \ b_3 = (q_3 = -1)\ {\rm XOR}\ (b_2= -1) = -1,$

  $b_4 = (q_4 = +1)\ {\rm XOR}\ (b_3= -1) = +1,\ \ b_5 = (q_5 = +1)\ {\rm XOR}\ (b_4= +1) = -1,\ \ b_6 = (q_6 = +1)\ {\rm XOR}\ (b_5= -1) = +1,\ \ b_7 = b_8 = \text{...} = -1.$

• With the initial condition  $b_0 = -1$  we get the negated sequence:  $b_4 = b_6 =-1$.  All others  $b_\nu = +1$.

(2)  Let  $b_0 = +1$.  Consider the AMI encoded sequence  $\langle c_\nu \rangle$  of the source symbol sequence  $\rm C$  and give their amplitude coefficients  $a_\nu$. 

• It holds:  $a_1= 0.5 \cdot (b_1-b_0) = -1$,  $a_2= 0.5 \cdot (b_2-b_1) =0$,  $a_3= 0. 5 \cdot (b_3-b_2) =0$,  $a_4= +1$,  $a_5= -1$,  $a_6= +1$,  $a_7= -1$,  $a_8= a_9 = \text{...} = 0$.
• In contrast to the pre–coding, the conventional addition (subtraction) is to be applied here and not the modulo–2 addition.

(3)  Now consider the AMI coding for several random sequences.  What rules can be derived from these experiments for the amplitude coefficients  $a_\nu$ ?

• Each binary value  "–1"  of   $q(t)$   ⇒   symbol  $\rm L$  is encoded by the ternary coefficient  $a_\nu = 0$.  Any number of  $a_\nu = 0$  can be consecutive.
• The binary value  "+1"  of   $q(t)$   ⇒   symbol  $\rm H$  is represented alternatively with   $a_\nu = +1$  and  $a_\nu = -1$ , starting with  $a_\nu = -1$,  if  $b_0 = +1$.
• From the source symbol sequence  $\rm A$   ⇒   $\langle \hspace{0.05cm}q_\nu \equiv +1 \hspace{0.05cm}\rangle$  the code symbol sequence  $+1, -1, +1, -1, \text{...}$ . Long sequences  $\langle \hspace{0.05cm}a_\nu \equiv +1 \hspace{0.05cm}\rangle$  or   $\langle \hspace{0.05cm}a_\nu \equiv -1 \hspace{0.05cm}\rangle$  are shot out.

(4)  Continue with  AMI  coding.  Interpret the autocorrelation function  $\varphi_a(\lambda)$  of the amplitude coefficients and the power density spectrum  ${\it \Phi}_a(f)$.

• The discrete ACF  $\varphi_a(\lambda)$  of the amplitude coefficients is only defined for integer  $\lambda$  values.   With AMI coding  $(N_{\rm C}=1)$  holds:   For  $|\lambda| > 1$   ⇒   all  $\varphi_a(\lambda)= 0$.
• $\varphi_a(\lambda = 0)$  is equal to the root mean square of the amplitude coefficients   ⇒   $\varphi_a(\lambda = 0) = {\rm Pr}(a_\nu = +1) \cdot (+1)^2 + {\rm Pr}(a_\nu = -1) \cdot (-1)^2 = 0.5.$
• Only the combinations  $(+1, -1)$  and  $(-1, +1)$  contribute to the expected value  ${\rm E}\big [a_\nu \cdot a_{\nu+1}\big]$   Result:  $\varphi_a(\lambda = \pm 1)={\rm E}\big [a_\nu \cdot a_{\nu+1}\big]=-0.25.$
• The power density spectrum  ${\it \Phi}_a(f)$  is the Fourier transform of the discrete ACF  $\varphi_a(\lambda)$.  Result:  ${\it \Phi}_a(f) = {1}/{2} \cdot \big [1 - \cos (2\pi f T)\big ] = \sin^2 (\pi f T)\hspace{0.05cm}.$
• From   ${\it \Phi}_a(f = 0) = 0$  follows:   The AMI code is especially interesting for channels over which no DC component can be transmitted.

(5)  We consider further AMI coding and rectangular pulses.  Interpret the ACF  $\varphi_s(\tau)$  of the transmission signal and the PDS  ${\it \Phi}_s(f)$.

• $\varphi_s(\tau)$  results from the convolution of the discrete AKF  $\varphi_a(\lambda)$  with  $\varphi^{^{\hspace{0.05cm}\bullet}}_{g}(\tau)$.   For rectangular pulses  $($duration $T)$:  The energy–AKF  $\varphi^{^{\hspace{0.05cm}\bullet}}_{g}(\tau)$  is a triangle of duration  $2T$.
• It holds  $\varphi_s(\tau = 0)= \varphi_a(\lambda = 0) =0.5, \ \varphi_s(\pm T)= \varphi_a( 1) =-0. 25,\ , \ \varphi_s( \pm 2T)= \varphi_a(2) =0.$  Between these discrete values, $\varphi_{s}(\tau)$  is always linear.
• The PDS  ${\it \Phi}_s(f)$  is obtained from  ${\it \Phi}_a(f) = \sin^2(\pi f T)$  by multiplying with  ${\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f) = {\rm sinc}^2(f T).$  This does not change anything at the zeros of  ${\it \Phi}_a(f)$ .

(6)  What changes with respect to  $s(t)$,  $\varphi_s(\tau)$  and  ${\it \Phi}_s(f)$  with the  $\rm Nyquist$  pulse?  Vary the roll–off factor here in the range  $0 \le r \le 1$.

• A single Nyquist pulse can be represented with the source symbol sequence  $\rm B$  in the  $s(t)$  range.  You can see equidistant zero crossings in the distance  $T$.
• Also, for any AMI random sequence, the signal values  $s(t=\nu \cdot T)$  for each  $r$  correspond exactly to their nominal positions.  Outside these points, there are deviations.
• In the special case  $r=0$  the energy–LDS  ${\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f)$  is constant in the range  $|f|<1/2T$.  Accordingly, the energy–ACF  ${\it \varphi}^{^{\hspace{0.08cm}\bullet}}_{g}(\tau)$  has a  $\rm sinc$  shape.
• On the other hand, for larger  $r$  the zeros of  ${\it \varphi}^{^{\hspace{0.08cm}\bullet}}_{g}(\tau)$  are no longer equidistant, since although  $G(f)$  satisfies the first Nyquist criterion, it does not  ${\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f)= [G(f)]^2$.
• The main advantage of the Nyquist pulse is the much smaller bandwidth.  Here only the frequency range  $|f| < (1+r)/(2T)$  has to be provided.

(7)  Repeat the last experiment using the  $\text{Root raised cosine}$  pulse instead of the Nyquist pulse.  Interpret the results.

• In the special case  $r=0$  the results are as in  (6). ${\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f)$  is constant in the range  $|f|<1/2T$  and outside zero;  ${\it \varphi}^{^{\hspace{0.08cm}\bullet}}_{g}(\tau)$  has a  $\rm sinc$  shape.
• Also for larger  $r$  the zeros of  ${\it \varphi}^{^{\hspace{0.08cm}\bullet}}_{g}(\tau)$  are eqidistant  (but not  $\rm sinc$  shaped)   ⇒   ${\it \Phi}^{^{\hspace{0.08cm}\bullet}}_{g}(f)= [G(f)]^2$  satisfies the first Nyquist criterion.
• On the other hand, $G(f)$  does not satisfy the first Nyquist criterion  $($except for  $r=0)$.  Intersymbol interference occurs already at the transmitter   ⇒   signal  $s(t)$.
• But this is also not a fundamental problem.  By using an identically shaped reception filter like  $G(f)$  intersymbol interference at the decider is avoided.

(8)  Consider and check the pre–coding  $(b_\nu)$  and the amplitude coefficients  $(a_\nu)$  with the  $\rm duobinary$  coding   $($source symbol sequence  $\rm C$,  $b_0 = +1)$.

• $b_1 = (q_1 = +1)\ {\rm XOR}\ (\overline{b_0}= -1) = +1,\ \ b_2 = (q_2 = -1)\ {\rm XOR}\ (\overline{b_1}= -1) = -1,\ \ b_3 = \text{...} =b_7 = +1,$  $b_8 = b_{10} = \text{...} =-1$,  $b_9 =b_{11} = \text{...}= +1$.
• $a_1= 0.5 \cdot (b_1+b_0) = +1$,  $a_2= 0.5 \cdot (b_2+b_1) =0$,  $a_3= 0.5 \cdot (b_3+b_2) = 0$,  $a_4= \text{...}= a_7=+1$,  $a_8=a_9= \text{...}= 0$.
• With the starting condition  $b_0 = -1$  we get again the negated sequence:     $a_1= -1$,  $a_2= a_3= 0$,  $a_4= \text{...}= a_7=-1$,  $a_8=a_9= \text{...}= 0$.

(9)  Now consider the Duobinary coding for several random sequences.  What rules can be derived from these experiments for the amplitude coefficients  $a_\nu$?

• The discrete ACF values are  $\varphi_a(\lambda = 0) = +0.5$,  $\varphi_a(\lambda = 1) = +0.25$,  $\varphi_a(\lambda = 2) = 0$   ⇒   ${\it \Phi}_a(f) = {1}/{2} \cdot \big [1 + \cos (2\pi f T)\big ] = \cos^2 (\pi f T)\hspace{0.05cm}.$
• Unlike the AMI coding, the encoded sequences  $\langle \hspace{0.05cm}a_\nu \equiv +1 \hspace{0.05cm}\rangle$  and   $\langle \hspace{0.05cm}a_\nu \equiv -1 \hspace{0.05cm}\rangle$  are possible here   ⇒   For the Duobinary code holds  ${\it \Phi}_a(f= 0) = 1 \ (\ne 0).$
• As with the AMI code, the "long zero sequence"   ⇒   $\langle \hspace{0.05cm}a_\nu \equiv 0 \hspace{0.05cm}\rangle$  is possible, which can again lead to synchronization problems.
• Excluded are the combinations  $a_\nu = +1, \ a_{\nu+1} = -1$  and   $a_\nu = -1, \ a_{\nu+1} = +1$,  recognizable by the PDS value  ${\it \Phi}_a(f= 1/(2T)) = 0.$
• Such direct transitions  $a_\nu = +1$   ⇒   $a_{\nu+1} = -1$  resp.   $a_\nu = -1$   ⇒   $a_{\nu+1} = +1$  lead to large intersymbol interference and thus to a higher error rate.

(10)  Compare the coding results of second order bipolar code  $\rm (BIP2)$  and first order bipolar code  $\rm (AMI)$  for different source symbol sequences.

• For a single rectangular pulse   ⇒   source symbol sequence  $\rm B$  both codes result in the same encoded sequence and the same encoded signal  $c(t)$   ⇒   also an isolated pulse.
• The "Permanent–One sequence"  $\rm A$  now results  $\langle c_\nu \rangle = \langle -1, -1, +1, +1, -1, -1, +1, +1, \text{. ..}\rangle $  instead of   $\langle c_\nu \rangle = \langle -1, +1, -1, +1, -1, +1, \text{...}\rangle $.
• The simple decoding algorithm of the AMI code  $($the ternary  $0$  becomes the binary  $-1$,  the ternary  $\pm 1$  becomes the binary  $+1)$  cannot be applied to  $\rm BIP2$ .

(11)  View and interpret the various ACF and LDS graphs of the  $\rm BIP2$  compared to the  $\rm AMI$  code.

• For  $\rm AMI$:   $\varphi_a(\lambda = \pm 1) = -0.25, \ \varphi_a(\lambda = \pm 2) = 0$.   For  $\rm BIP2$:   $\varphi_a(\lambda = \pm 1) = 0, \ \varphi_a(\lambda = \pm 2) = -0.25$.  In both cases:  $\varphi_a(\lambda = 0) = 0.5$.
• From the  $\rm AMI$ power density spectrum  ${\it \Phi}_a(f) = \sin^2 (\pi \cdot f T)$  follows for  $\rm BIP2$:  ${\it \Phi}_a(f) = \sin^2 (2\pi \cdot f T)$  by compression with respect to the  $f$–axis.
• Zero at  $f=0$:  At most two  $+1$  directly follow each other, and also at most only two  $-1$.  In the AMI code  $+1$  and  $-1$  occur only in isolation.
• Next zero at  $f=1/(2T)$:  The infinitely long  $(+1, -1)$  sequence is excluded in  $\rm BIP2$  as in the  $\rm Duobinary$  code.
• Consider and interpret also the functions  $\varphi_s(\tau)$  and  ${\it \Phi}_s(f)$  for the pulses "rectangle", "Nyquist" and "Root raised cosine".

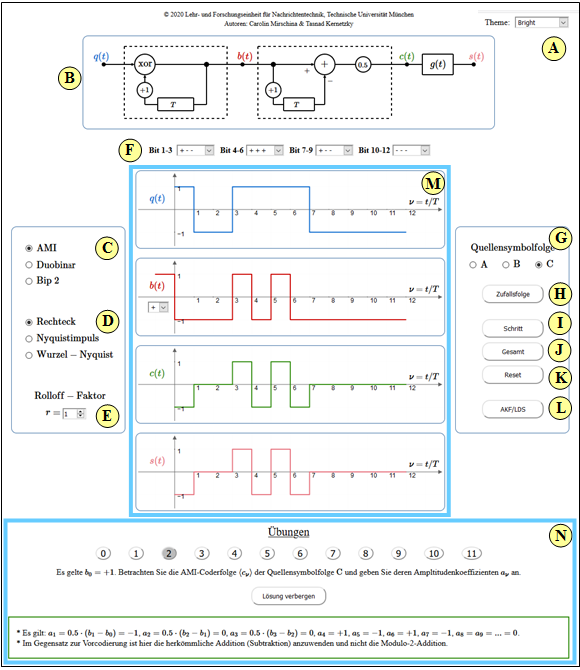
Applet Manual

Bildschirmabzug (deutsche Version, heller Hintergrund)

    (A)     Theme (veränderbare grafische Oberflächengestaltung)

• Dark:   schwarzer Hintergrund  (wird von den Autoren empfohlen)
• Bright:   weißer Hintergrund  (empfohlen für Beamer und Ausdrucke)
• Deuteranopia:   für Nutzer mit ausgeprägter Grün–Sehschwäche
• Protanopia:   für Nutzer mit ausgeprägter Rot–Sehschwäche

    (B)     Zugrundeliegendes Blockschaltbild

    (C)     Auswahl des Pseudoternörcodes:
                   AMI–Code, Duobinärcode, Bipolarcode 2. Ordnung

    (D)     Auswahl des Grundimpulses  $g(t)$:
                   Rechteckimpuls, Nyquistimpuls, Wurzel–Nyquistimpuls

    (E)     Rolloff–Faktor (Frequenzbereich) für "Nyquist" und "Wurzel–Nyquist"

    (F)     Einstellung von  $3 \cdot 4 = 12$  Bit der Quellensymbolfolge

    (G)     Auswahl einer drei voreingestellten Quellensymbolfolgen

    (H)     Zufällige binäre Quellensymbolfolge

    ( I )     Schrittweise Verdeutlichung der Pseudoternärcodierung

    (J)     Ergebnis der Pseudoternärcodierung:  Signale  $q(t)$,  $b(t)$,  $c(t)$,  $s(t)$

    (K)     Löschen der Signalverläufe im Grafikbereich  $\rm M$

    (L)     Skizzen für Autokorrelationsfunktion & Leistungsdichtespektrum

    (M)     Grafikbereich:  Quellensignal  $q(t)$, Signal  $b(t)$  nach Vorcodierung,
                   Codersignal  $c(t)$  mit Rechtecken, Sendesignal  $s(t)$  gemäß  $g(t)$

    (N)     Bereich für Übungen:  Aufgabenauswahl, Fragen, Musterlösung

About the Authors

This interactive calculation tool was designed and implemented at the  Institute for Communications Engineering  at the  Technical University of Munich.

• The first version was created in 2010 by  Stefan Müller    as part of his diploma thesis with “FlashMX – Actionscript” (Supervisor: Günter Söder).
• In 2020 the program was redesigned by  Carolin Mirschina  as part of her bachelor thesis  (Supervisor: Tasnád Kernetzky ) via "HTML5".
• Last revision and English version 2021 by  Carolin Mirschina  in the context of a working student activity. 

The conversion of this applet to HTML 5 was financially supported by  "Studienzuschüsse"  (Faculty EI of the TU Munich).  We thank.

Once again: Open Applet in new Tab

Open Applet in new Tab   Deutsche Version Öffnen