Exercise 2.6Z: Synchronous Demodulator

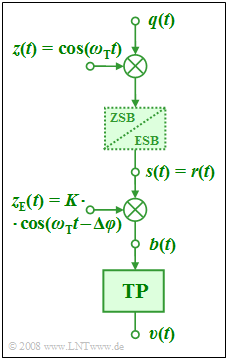
Das dargestellte Blockschaltbild zeigt ein Übertragungssystem mit Zweiseitenband-Amplitudenmodulation (ZSB-AM) und Synchrondemodulator (SD). Das Quellensignal bestehe aus zwei harmonischen Schwingungen mit den Frequenzen $f_2 = 2 \ \rm kHz$ und $f_5 = 5 \ \rm kHz$: $$q(t) = {2 \, \rm V} \cdot {\rm cos}(\omega_2 t )+ {1 \, \rm V} \cdot {\rm sin}(\omega_5 t ) .$$

Dieses Signal wird mit dem dimensionslosen Trägersignal $z(t) = \cos(\omega_{\rm T} \cdot T)$ der Trägerfrequenz $f_{\rm T} = 50 \ \rm kHz$ multipliziert. Bei ZSB–AM ist der gestrichelt eingezeichnete Block unerheblich, so dass für das Sendesignal gilt:

$$s(t) = q(t) \cdot {\rm cos}(\omega_{\rm T} t ) .$$

Im Synchrondemodulator wird das Empfängersignal $r(t)$, das bei idealem Kanal identisch mit $s(t)$ ist, mit dem empfangsseitigem Trägersignal $z_{\rm E}(t)$ multipliziert, wobei gilt:

$$z_{\rm E}(t) = K \cdot {\rm cos}(\omega_{\rm T} t - \Delta \varphi ) .$$

Dieses Signal sollte nicht nur frequenzsynchron mit $z(t)$ sein, sondern auch phasensynchron – daher der Name „Synchrondemodulator”. Der obige Ansatz berücksichtigt einen Phasenversatz zwischen $z(t)$ und $z_{\rm E}(t)$, der idealerweise $\Delta \varphi = 0$ sein sollte, sich bei realen Systemen aber oft nicht vermeiden lässt.

Das Ausgangssignal $b(t)$ des zweiten Multiplizierers beinhaltet neben dem gewünschten NF-Anteil auch Anteile um die doppelte Trägerfrequenz. Durch einen idealen Tiefpass – z.B. mit der Grenzfrequenz $f_{\rm T}$ – lässt sich das Sinkensignal $v(t)$ gewinnen, das im Idealfall gleich dem Quellensignal $q(t)$ sein sollte.

Die Multiplikation beim Sender mit dem Trägersignal $z(t)$ führt im Allgemeinen zu zwei Seitenbändern. Bei der Einseitenbandmodulation (ESB–AM) wird nur eines der beiden Bänder übertragen, zum Beispiel das untere Seitenband (USB). Damit erhält man bei idealem Kanal:

$$r(t) = s(t)= {1 \, \rm V} \cdot {\rm cos}((\omega_{\rm T} - \omega_2 )t ) - {0.5 \, \rm V} \cdot {\rm sin}((\omega_{\rm T} - \omega_5 )t ) .$$

Hier führt die Synchrondemodulation unter Berücksichtigung eines Phasenversatzes $\Delta \varphi$, der Konstante $K = 4$ sowie des nachgeschalteten Tiefpasses zu folgendem verfälschten Sinkensignal:

$$v(t)= {1 \, \rm V} \cdot \frac{1}{2}\cdot 4 \cdot{\rm cos}( \omega_2 t - \Delta \varphi)+ {0.5 \, \rm V} \cdot \frac{1}{2}\cdot 4 \cdot{\rm sin}( \omega_5 t - \Delta \varphi)$$

$$\Rightarrow \hspace{0.5cm}v(t)= {2 \, \rm V} \cdot{\rm cos}( \omega_2 t - \Delta \varphi)+ {1 \, \rm V} \cdot{\rm sin}( \omega_5 t - \Delta \varphi)$$

Im Idealfall phasensynchroner Demodulation (Δφ = 0) gilt wieder $v(t) = q(t).$

Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 2.3 in diesem Buch. Die Thematik „Amplitudenmodulation/Synchrondemodulator” wird im Buch Modulationsverfahren noch ausführlich diskutiert werden.

Gegeben sind die folgenden trigonometrischen Zusammenhänge:

$$\cos^2(\alpha) = \frac{1}{2} \cdot \left [ 1 + \cos(2\alpha) \right ] \hspace{0.05cm}, \\ \cos(\alpha) \cdot \cos(\beta) = \frac{1}{2} \cdot \left[ \cos(\alpha - \beta)+ \cos(\alpha + \beta) \right] \\ \sin(\alpha) \cdot \cos(\beta) = \frac{1}{2} \cdot \left[ \sin(\alpha - \beta)+ \sin(\alpha + \beta) \right] \hspace{0.05cm}.$$

Fragebogen

Musterlösung

Solution

1. Für das Bandpass–Signal nach dem zweiten Multiplizierer gilt:

$$b(t) = r(t) \cdot z_{\rm E}(t)= q(t) \cdot z(t) \cdot z_{\rm E}(t)= K \cdot q(t)\cdot \cos^2(\omega_{\rm T} t).$$

Mit der trigonometrischen Beziehung

$$\cos^2(\omega_{\rm T} t) = \frac{1}{2} \cdot\left[ 1 + \cos(2\omega_{\rm T} t)\right]$$

erhält man

$$b(t) = \frac{K}{2} \cdot q(t) + \frac{K}{2} \cdot q(t)\cdot \cos(2\omega_{\rm T} t).$$

Der zweite Anteil liegt um die doppelte Trägerfrequenz und wird durch den Tiefpass – zum Beispiel mit der Grenzfrequenz f_T – entfernt. Damit erhält man:

$$v(t) = \frac{K}{2} \cdot q(t) .$$

Mit K = 2 ergibt sich eine ideale Demodulation:

$$v(t) = q(t) .$$

2. Unter Berücksichtigung der Beziehung

$$\cos(\omega_{\rm T} t) \cdot \cos(\omega_{\rm T} t - \Delta \varphi) = \frac{1}{2} \cdot \left[ \cos(\Delta \varphi)+ \cos(2\omega_{\rm T} t - \Delta \varphi) \right]$$

sowie des nachgeschalteten Tiefpasses, der wieder den Anteil um die doppelte Trägerfrequenz entfernt, erhält man hier mit K = 2:

$$v(t) = q(t) \cdot \cos(\Delta \varphi).$$

Das heißt, ein Phasenversatz Δφ führt hier nur zu einer frequenzunabhängigen Dämpfung und nicht zu Dämpfungs– oder Phasenverzerrungen. Ein Phasenversatz um ±60° hat jeweils eine Halbierung des Signals zur Folge. Richtig sind demnach die Lösungsvorschläge 2 und 5.

3. Richtig ist hier der Lösungsvorschlag 4. Bei beiden Summanden tritt genau der gleiche Phasenversatz Δφ auf, und es kommt hier zu Phasenverzerrungen:

$$v(t)= {2 \, \rm V} \cdot{\rm cos}( \omega_2 \cdot (t - \tau_2))+ {1 \, \rm V} \cdot{\rm sin}( \omega_5 t \cdot (t - \tau_5)),$$

$${\rm wobei}\hspace{0.5cm}\tau_2 = \frac{\Delta \varphi}{\omega_2} \hspace{0.5cm}\ne \hspace{0.5cm} \tau_5 = \frac{\Delta \varphi}{\omega_5}.$$

Ein Phasenversatz von 60° entsprechend π/3 führt hier zu den Verzögerungszeiten:

$$\tau_2 = \frac{\pi/3}{2 \pi \cdot 2\,\,{\rm kHz }} \approx 83.3\,{\rm \mu s }, \hspace{0.5cm} \tau_5 = \frac{\pi/3}{2 \pi \cdot 5\,\,{\rm kHz }} \approx 33.3\,{\rm \mu s }.$$

Das niederfrequentere Signal wird also stärker verzögert.

	Unabhängig von Δφ gilt υ(t) = q(t).
	Δφ ≠ 0 führt zu einer frequenzunabhängigen Dämpfung.
	Ein Phasenversatz Δφ ≠ 0 führt zu Dämpfungsverzerrungen.
	Ein Phasenversatz Δφ ≠ 0 führt zu Phasenverzerrungen.
	Mit Δφ = – 60° gilt υ(t) = q(t)/2.

	Unabhängig von Δφ gilt υ(t) = q(t).
	Δφ ≠ 0 führt zu einer frequenzunabhängigen Dämpfung.
	Ein Phasenversatz Δφ ≠ 0 führt zu Dämpfungsverzerrungen.
	Ein Phasenversatz Δφ ≠ 0 führt zu Phasenverzerrungen.
	Mit Δφ = – 60° gilt υ(t) = q(t)/2.