Contents
Betrachtetes Systemmodell
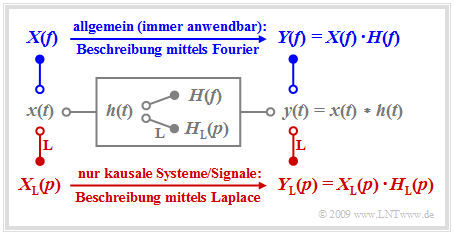
Wir betrachten ein lineares zeitinvariantes System mit der Impulsantwort $h(t)$, an dessen Eingang das Signal $x(t)$ anliegt. Das Ausgangssignal $y(t)$ ergibt sich dann als das Faltungsprodukt $x(t) ∗ h(t)$.
Bei akausalen Systemen und Signalen muss zur Beschreibung des Spektralverhaltens stets das erste Fourierintegral angewendet werden, und es gilt für das Ausgangsspektrum: $$Y(f) = X(f) \cdot H(f) \hspace{0.05cm}.$$ Das Fourierintegral besitzt auch für kausale Systeme und Signale, also unter der Voraussetzung $$x(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} t<0\hspace{0.05cm},\hspace{0.2cm} h(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} t<0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} y(t) = 0 \hspace{0.2cm}{\rm{f\ddot{u}r}} \hspace{0.2cm} t<0 \hspace{0.05cm}$$ weiterhin Gültigkeit. In diesem Fall ergeben sich aber durch Anwendung der Laplace–Transformation unter Beachtung gewisser Restriktionen wesentliche Vorteile:
- Die so behandelten Systeme sind stets durch eine Schaltung realisierbar. Der Entwickler kommt nicht in Versuchung, realitätsfremde Lösungen anzubieten.
- Die Laplace–Transformierte $X_{\rm L}(p)$ ist stets eine reelle Funktion der Spektralvariablen $p$. Dass sich diese Variable entsprechend $p = {\rm j} · 2πf$ aus der Multiplikation der physikalischen Kreisfrequenz $ω = 2πf$ mit der imaginären Einheit j ergibt, spielt für den Anwender keine Rolle.
- Die implizite Bedingung $x(t) = 0$ für $t < 0$ erlaubt speziell die Analyse des Einschwingverhaltens nach Einschaltvorgängen in einfacherer Weise als mit dem Fourierintegral.
Definition der Laplace–Transformation
Ausgehend vom ersten Fourierintegral $$X(f) = \int_{-\infty}^{+\infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-{\rm j}\hspace{0.05cm} 2\pi f t}}\hspace{0.1cm}{\rm d}t$$ ergibt sich bei einer kausalen Zeitfunktion (wenn also gilt: $x(t) = 0$ für $t < 0$) mit der formalen Substitution $p = {\rm j} · 2πf$ direkt die Laplace–Transformation.
Die Laplace–Transformierte einer kausalen Zeitfunktion $x(t)$ lautet: $$X_{\rm L}(p) = \int_{0}^{\infty} { x(t) \hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-p t}}\hspace{0.1cm}{\rm d}t\hspace{0.05cm}, \hspace{0.3cm}{\rm kurz}\hspace{0.3cm} X_{\rm L}(p) \quad \bullet\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\circ\quad x(t)\hspace{0.05cm}.$$
Der Zusammenhang zwischen der Laplace–Transformierten $X_{\rm L}(p)$ und dem physikalischen Spektrum $X(f)$ ist häufig wie folgt gegeben:
$$X(f) = X_{\rm L}(p) \Bigg |_{{\hspace{0.1cm} p\hspace{0.05cm}={\rm \hspace{0.05cm} j\hspace{0.05cm}2\pi \it f}}}.$$
Beinhaltet allerdings das Signal $x(t)$ periodische Anteile und damit die Spektralfunktion $X(f)$ zusätzliche Diracfunktionen, so ist diese Gleichung nicht anwendbar. In diesem Fall muss $p = α + {\rm j} · 2πf$ angesetzt werden und es ist dann der Grenzübergang $α → 0$ zu bilden.
Wir gehen von der einseitig exponentiell abfallenden Zeitfunktion entsprechend der Skizze in einem früheren Beispiel aus: $$x(t) = \left\{ \begin{array}{c} 0 \\ 0.5 \\ {\rm e}^{-t/T} \end{array} \right.\quad \quad \begin{array}{c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \end{array}\begin{array}{*{20}c}{ t < 0\hspace{0.05cm},} \\ { t = 0\hspace{0.05cm},} \\{ t > 0\hspace{0.05cm}.} \end{array}$$ Damit lautet die Laplace–Transformierte: $$X_{\rm L}(p) = \int_{0}^{\infty} { {\rm e}^{-t/T}}\hspace{0.1cm}{\rm d}t= \frac {1}{p + 1/T} \cdot {{\rm e}^{-(p+1/T) \hspace{0.05cm}\cdot \hspace{0.05cm}t}}\hspace{0.05cm}\Bigg |_{t \hspace{0.05cm}=\hspace{0.05cm} 0}^{\infty}= \frac {1}{p + 1/T} \hspace{0.05cm} .$$ Mit $p = {\rm j} · 2πf$ erhält man die herkömmliche Spektralfunktion bezüglich $f$: $$X(f) = \frac {1}{{\rm j \cdot 2\pi \it f} + 1/T} = \frac {T}{1+{\rm j \cdot 2\pi \it fT}} \hspace{0.05cm} .$$ Betrachtet man dagegen den Frequenzgang eines Tiefpasses erster Ordnung, dessen Impulsantwort $h(t)$ sich gegenüber der obigen Zeitfunktion um den Faktor $1/T$ unterscheidet, so gilt für die Laplace–Transformierte bzw. die Fourier–Transformierte: $$H_{\rm L}(p)= \frac {1/T}{p + 1/T}= \frac {1}{1 + p \cdot T} \hspace{0.05cm} , \hspace{0.8cm}H(f) = \frac {1}{1+{\rm j \cdot 2\pi \it fT}} \hspace{0.05cm} .$$ Häufig verwendet man dann anstelle des Parameters $T$ die 3dB–Grenzfrequenz $f_{\rm G} = 1/(2πT)$.
Einige wichtige Laplace–Korrespondenzen
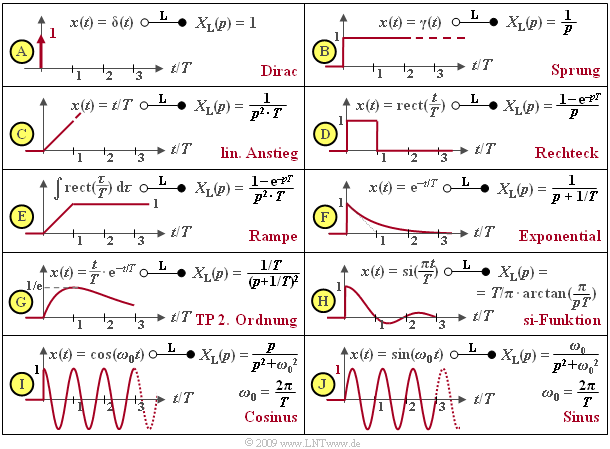
Unten sind einige wichtige Laplace–Korrespondenzen zusammengestellt. Die Laplace–Transformierte der Diracfunktion $δ(t)$ ist $X_{\rm L}(p) = 1$ (Diagramm A). Durch Anwendung des Integrationssatzes erhält man für die Sprungfunktion $X_{\rm L}(p) = 1/p$ (Diagramm B) und aus dieser durch Multiplikation mit $1/(pT)$ die Laplace–Transformierte der linear ansteigenden Funktion $x(t) = t/T$ für $t > 0$ (Diagramm C).
Die Rechteckfunktion kann aus der Subtraktion zweier um $T$ auseinanderliegender Sprungfunktionen $γ(t)$ und $γ(t – T)$ erzeugt werden, so dass sich nach dem Verschiebungssatz die Laplace–Transformierte $X_{\rm L}(p) = (1 – {\rm e}^{–pT})/p$ ergibt (Diagramm D). Durch Integration erhält man daraus die Rampenfunktion bzw. nach Multiplikation mit $1/(pT)$ deren Laplace–Transformierte (Diagramm E).
Die Exponentialfunktion (Diagramm F) wurde bereits auf der letzten Seite betrachtet. Mit dem Faktor $1/T$ beschreibt diese gleichzeitig die Impulsantwort eines Tiefpasses erster Ordnung. Durch Quadrierung erhält man die $p$–Spektralfunktion eines Tiefpasses zweiter Ordnung. Die zugehörige Zeitfunktion lautet $x(t) = t/T · {\rm e}^{–t/T}$ (Diagramm G).
Neben der kausalen si–Funktion (Diagramm H) sind in der Tabelle auch die Laplace–Transformierten der kausalen Cosinus– und Sinusfunktion (Diagramme I und J) angegeben, die sich zu $p/(p^2 + ω_0^2)$ bzw. $ω_0/(p^2 + ω_0^2)$ ergeben. Hierbei bezeichnet $ω_0 = 2πf_0 = 2π/T$ die so genannte Kreisfrequenz.
Alle hier betrachteten Zeitsignale $x(t)$ sind dimensionslos angenommen. Aus diesem Grund besitzt $X_{\rm L}(p)$ als das Integral über die Zeit stets die Einheit „Sekunde”.
Pol–Nullstellen–Darstellung von Schaltungen
Ein jedes lineare zeitinvariante (LZI–) System, das durch eine Schaltung aus diskreten zeitkonstanten Bauelementen wie Widerständen $(R)$, Kapazitäten $(C)$, Induktivitäten $(L)$ und Verstärkerelementen realisiert werden kann, besitzt eine gebrochen–rationale $p$–Übertragungsfunktion: $$H_{\rm L}(p)= \frac {A_Z \cdot p^Z + ... + A_2 \cdot p^2 + A_1 \cdot p + A_0} {B_N \cdot p^N + ... + B_2 \cdot p^2 + B_1 \cdot p + B_0}= \frac {Z(p)}{N(p)} \hspace{0.05cm} .$$
Alle Koeffizienten des Zählers ⇒ $A_Z, ..., A_0$ und des Nenners ⇒ $B_N, ..., B_0$ sind reell. Weiter bezeichnen
- $Z$ den Grad des Zählerpolynoms $Z(p)$,
- $N$ den Grad des Nennerpolynoms $N(p)$.
Eine äquivalente Pol–Nullstellen–Darstellung der obigen Übertragungsfunktion lautet:
$$H_{\rm L}(p)= K \cdot \frac {\prod\limits_{i=1}^Z p - p_{\rm o i}} {\prod\limits_{i=1}^N p - p_{\rm x i}}= K \cdot \frac {(p - p_{\rm o 1})(p - p_{\rm o 2})\cdot ... \cdot (p - p_{{\rm o} \hspace{-0.03cm} Z})} {(p - p_{\rm x 1})(p - p_{\rm x 2})\cdot ... \cdot (p - p_{{\rm x} \hspace{-0.03cm} N})} \hspace{0.05cm} .$$
Die $Z + N +$ 1 Parameter bedeuten:
- $K = A_Z/B_N$ ist ein konstanter Faktor. Gilt $Z = N$, so ist dieser dimensionslos.
- Die Lösungen der Gleichung $Z(p) = 0$ ergeben die $Z$ Nullstellen $p_{o1}, ..., p_{oZ}$ von $H_{\rm L}(p)$.
- Die Nullstellen des Nennerpolynoms $N(p)$ liefern die $N$ Polstellen (oder kurz Pole).
Die Umformung ist eindeutig. Dies erkennt man daran, dass die obere Übertragungsfunktion ebenfalls nur durch $Z + N + 1$ freie Parameter bestimmt ist, da einer der Koeffizienten $A_Z, ... , A_0, B_N, ... , B_0$ ohne Änderung des Quotienten auf $1$ normiert werden kann.
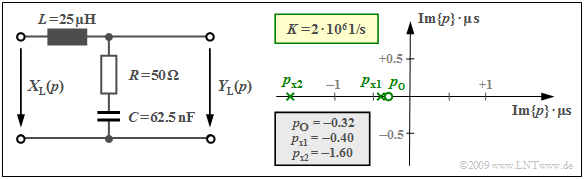
Wir betrachten den gezeichneten Vierpol mit einer Induktivität $L$ (komplexer Widerstand $pL$) im Längszweig sowie im Querzweig die Serienschaltung eines Ohmschen Widerstandes $R$ und einer Kapazität $C$ mit dem komplexen Widerstand $1/(pC)$.
Damit lautet die $p$–Übertragungsfunktion: $$H_{\rm L}(p)= \frac {Y_{\rm L}(p)} {X_{\rm L}(p)}= \frac {R + {1}/{(pC)}} {pL + R +{1}/{(pC)}}= \frac {1 + p \cdot{RC}} {1 + p \cdot{RC}+ p^2 \cdot{LC}} \hspace{0.05cm} .$$ Setzt man $p = {\rm j} · 2πf$ ein, so erhält man die Fourier–Übertragungsfunktion (bzw. den Frequenzgang). Dividiert man in obiger Gleichung Zähler und Nenner durch $LC$, so ergibt sich: $$H_{\rm L}(p)= \frac {R} {L}\cdot \frac {p + {1}/{(RC)}} {p^2 + {R}/ {L}\cdot p + {1}/{(LC)}}= K \cdot \frac {p - p_{\rm o }} {(p - p_{\rm x 1})(p - p_{\rm x 2})} \hspace{0.05cm} .$$
Im rechten Gleichungsteil ist die Übertragungsfunktion $H_{\rm L}(p)$ in Pol–Nullstellen–Notation angegeben. Durch Koeffizientenvergleich ergeben sich für $R = 50 \ \rm Ω$, $L = 25\ \rm μH$ und $C = 62.5 \ \rm nF$ folgende Werte:
- die Konstante $K = R/L = 2 · 10^6 \cdot 1/{\rm s}$,
- die Nullstelle $p_o = –1/(RC) = –0.32 · 10^6 \cdot 1/{\rm s},$
- die beiden Pole $p_{x1}$ und $p_{x2}$ als Lösung der Gleichung
$$p^2 + \frac {R} {L}\cdot p + \frac{1}{LC} = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x 1,\hspace{0.05cm}2 }= -\frac {R} {2L}\pm \sqrt{\frac {R^2} {4L^2}- \frac{1}{LC}}$$ $$\Rightarrow \hspace{0.3cm} p_{\rm x 1,\hspace{0.05cm}2 }= -10^6 \cdot {1}/{\rm s} \pm \sqrt{10^{12} \cdot {1} /{\rm s^2}-0.64 \cdot 10^{12} \cdot {1}/ {\rm s^2}}$$ $$\Rightarrow \hspace{0.3cm} p_{\rm x 1 }= -0.4 \cdot 10^6\cdot {1}/ {\rm s},\hspace{0.2cm}p_{\rm x 2 }= -1.6 \cdot 10^6\cdot {1}/ {\rm s} \hspace{0.05cm} .$$ In der obigen Grafik ist rechts das Pol–Nullstellen–Diagramm angegeben. Die beiden Achsen bezeichnen den Real– und den Imaginärteil der Variablen $p$, jeweils normiert auf den Wert $10^6 · \rm 1/s\; (= 1/μs)$. Man erkennt nach dieser Normierung die Nullstelle bei $p_{\rm o} =\, –0.32$ als Kreis und die beiden Polstellen bei $p_{\rm x1} = \,–0.4$ und $p_{\rm x2} = \,–1.6$ als Kreuze.
Eigenschaften der Pole und Nullstellen
Die Übertragungsfunktion $H_{\rm L}(p)$ einer jeden realisierbaren Schaltung wird durch $Z$ Nullstellen und $N$ Pole zusammen mit einer Konstanten $K$ vollständig beschrieben, wobei folgende Einschränkungen gelten:
- Es gilt stets $Z ≤ N$. Mit $Z > N$ würde sich im Grenzfall für $p → ∞$ (also für sehr hohe Frequenzen) auch eine „unendlich große” $p$–Übertragungsfunktion ergeben.
- Die Nullstellen $p_{\rm oi}$ und die Pole $p_{\rm xi}$ sind im allgemeinen komplex und weisen wie $p$ die Einheit $\rm 1/s$ auf. Gilt $Z < N$, so besitzt auch die Konstante $K$ eine Einheit.
- Die Pole und Nullstellen können reell sein, wie im letzten Beispiel gezeigt. Sind sie komplex, so treten immer zwei konjugiert–komplexe Polstellen bzw. zwei konjugiert–komplexe Nullstellen auf, da $H_{\rm L}(p)$ stets eine reelle gebrochen–rationale Funktion darstellt.
- Alle Pole liegen in der linken Halbebene oder – als Grenzfall – auf der imaginären Achse. Diese Eigenschaft ergibt sich aus der erforderlichen und vorausgesetzten Kausalität zusammen mit dem Hauptsatz der Funktionstheorie, der im nächsten Kapitel angegeben wird.
- Nullstellen können sowohl in der linken als auch in der rechten $p$–Halbebene auftreten oder auch auf der imaginären Achse. Ein Beispiel für Nullstellen in der rechten Halbebene findet man in der Zusatzaufgabe 3.4Z, die sich mit Allpässen beschäftigt.
- Bei den so genannten Minimum–Phasen–Systemen sind in der rechten $p$–Halbebene nicht nur Pole verboten, sondern auch Nullstellen. Der Realteil aller Singularitäten ist hier nie positiv.
Diese Eigenschaften werden nun an drei Beispielen verdeutlicht.
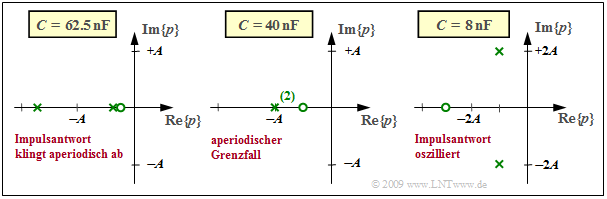
Ausgehend von der bereits im letzten Abschnitt betrachteten Vierpolschaltung $(L$ im Längszweig, $R$ und $C$ im Querzweig) können die charakteristischen Größen der Übertragungsfunktion wie folgt angegeben werden: $$K = 2A, \hspace{0.2cm}p_{\rm x 1,\hspace{0.05cm}2 }= -A \pm \sqrt{A^2-B^2}, \hspace{0.2cm}p_{\rm o }= - \frac{B^2}{2A} \hspace{0.05cm} \hspace{0.2cm} {\rm mit } \hspace{0.2cm} A = \frac {R} {2L}, \hspace{0.2cm}B = \frac{1}{\sqrt{LC}} \hspace{0.05cm}.$$ Die in der Grafik genannten Kapazitätswerte $C$ gelten für $R = 50 \ \rm Ω$ und $L = 25 \ \rm μH$. Die Achsen sind auf die Variable $A = R/(2L) = 10^6 · \rm 1/s$ normiert, und es gilt $K = 2A = 2 · 10^6 · \rm 1/s.$
Die Grafik zeigt drei verschiedene Diagramme. Der konstante Faktor ist jeweils $K = 2 · 10^6 · \rm 1/s:$
- Für $B < A$ erhält man zwei reelle Pole und eine Nullstelle rechts von $–A/2$. Beispielsweise ergibt sich für $C = 62.5 \ \rm nF$ entsprechend dem linken Diagramm:
$$ {B}/ {A}= 0.8 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x 1}/A = -0.4 , \hspace{0.2cm}p_{\rm x 2}/A= -1.6 , \hspace{0.2cm}p_{\rm o}/A= -0.32 \hspace{0.05cm} .$$
- Für $B > A$ ergeben sich zwei konjugiert–komplexe Pole und eine Nullstelle links von $–A/2$, zum Beispiel gemäß dem rechten Diagramm für $C = 8 \ \rm nF$:
$${B}/ {A}= \sqrt{5} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x 1,\hspace{0.05cm}2 }/A= -1\pm {\rm j}\cdot 2,\hspace{0.2cm}p_{\rm o}/A\approx -2.5 \hspace{0.05cm} .$$
- Der Grenzfall $A = B$ führt zu einer reellen doppelten Polstelle und einer Nullstelle bei $– A/2$ (siehe mittleres Diagramm, gültig für $C = 400 \ \rm nF$):
$$ {B}/ {A}= 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm x 1}/A= p_{\rm x 2}/A= -1, \hspace{0.2cm}p_{\rm o}/A= -0.5 \hspace{0.05cm} .$$
Die Impulsantworten sind entsprechend dem nachfolgenden Kapitel Laplace–Rücktransformation
- aperiodisch abklingend (linkes Diagramm),
- oszillierend (rechtes Diagramm), oder
- man spricht vom aperiodischen Grenzfall (mittleres Diagramm).
Grafische Ermittlung von Dämpfung und Phase
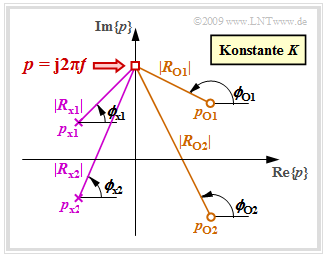
Gegeben sei die $p$–Übertragungsfunktion in der Pol–Nullstellen–Notation: $$H_{\rm L}(p)= K \cdot \frac {\prod\limits_{i=1}^Z (p - p_{\rm o i})} {\prod\limits_{i=1}^N (p - p_{\rm x i})}= K \cdot \frac {(p - p_{\rm o 1})(p - p_{\rm o 2})\cdot ... \cdot (p - p_{ {\rm o} \hspace{-0.03cm} Z})} {(p - p_{\rm x 1})(p - p_{\rm x 2})\cdot ... \cdot (p - p_{ {\rm x} \hspace{-0.03cm} N})} \hspace{0.05cm} .$$ Zur herkömmlichen Übertragungsfunktion bzw. zum Frequenzgang $H(f)$ kömmt man, indem man das Argument $p$ der Funktion $H_{\rm L}(p)$ durch j · $2πf$ ersetzt: $$H(f)= K \cdot \frac {({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm o 1})({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm o 2})\cdot ... \cdot ({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm o} \hspace{-0.03cm} Z})} {({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm x 1})({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{\rm x 2})\cdot ... \cdot ({\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm x} \hspace{-0.03cm} N})} \hspace{0.05cm} .$$ Wir betrachten nun eine feste Frequenz $f$ und beschreiben die Abstände und Winkel aller Nullstellen durch Vektoren: $$R_{ {\rm o} i} = {\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm o} i}= |R_{{\rm o} i}| \cdot {\rm exp}({\hspace{0.03cm}{\rm j}\cdot\phi_{ {\rm o} i} }), \hspace{0.3cm}i= 1, ... , Z \hspace{0.05cm} .$$ In gleicher Weise gehen wir für die Polstellen vor: $$R_{ {\rm x} i} = {\rm j} \cdot 2\pi \hspace{-0.05cm}f - p_{ {\rm x} i}= |R_{ {\rm x} i}| \cdot {\rm exp}({\hspace{0.03cm}{\rm j}\cdot\phi_{ {\rm x} i} }), \hspace{0.3cm}i= 1, ... , N \hspace{0.05cm} .$$ Die nachfolgende Grafik zeigt die Beträge und Phasenwinkel für ein System mit $Z =$ 2 Nullstellen in der rechten Halbebene und $N =$ 2 Polstellen in der linken Halbebene. Zu berücksichtigen ist zudem die Konstante $K$.
Mit dieser Vektordarstellung kann für den Frequenzgang geschrieben werden: $$H(f)= K \cdot \frac {|R_{ {\rm o} 1}| \cdot |R_{ {\rm o} 2}|\cdot ... \cdot |R_{ {\rm o} \hspace{-0.03cm} Z}|} {|R_{ {\rm x} 1}| \cdot |R_{ {\rm x} 2}|\cdot ... \cdot |R_{ {\rm x} \hspace{-0.03cm} N}|} \cdot {\rm e^{\hspace{0.03cm}{\rm j} \hspace{0.05cm}\cdot [ \phi_{ {\rm o} 1}\hspace{0.1cm}+ \hspace{0.1cm}\phi_{ {\rm o} 2} \hspace{0.1cm}+ \hspace{0.1cm}\hspace{0.1cm}... \hspace{0.1cm} + \hspace{0.1cm}\phi_{ {\rm o} \hspace{-0.03cm}{\it Z}}\hspace{0.1cm}- \hspace{0.1cm}\phi_{ {\rm x} 1}\hspace{0.1cm}- \hspace{0.1cm}\phi_{ {\rm x} 2} \hspace{0.1cm}- \hspace{0.1cm}... \hspace{0.1cm} - \hspace{0.1cm} \phi_{ {\rm x} \hspace{-0.03cm}{\it N} }]} } \hspace{0.05cm} .$$ Die Bildbeschreibung wird nachfolgend fortgesetzt.
Stellt man $H(f)$ durch die Dämpfung $a(f)$ und die Phase $b(f)$ entsprechend der allgemeinen Beziehung
$$H(f) = {\rm e}^{-a(f)\hspace{0.05cm}- \hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}b(f)}$$
dar, so erhält man durch den Vergleich mit der obigen Gleichung das folgende Ergebnis:
- Unter der Voraussetzung, dass alle dimensionsbehafteten Größen geeignet normiert sind, gilt für die Dämpfung in Neper (1 Np ist gleich 8.686 dB):
$$a(f) = -{\rm ln} \hspace{0.1cm} K + \sum \limits_{i=1}^N {\rm ln} \hspace{0.1cm} |R_{ {\rm x} i}|- \sum \limits_{i=1}^Z {\rm ln} \hspace{0.1cm} |R_{ {\rm o} i}| \hspace{0.05cm} .$$
- Die Phasenfunktion in Radian (rad) ergibt sich entsprechend der Skizze im letzten Abschnitt zu
$$b(f) = \phi_K + \sum \limits_{i=1}^N \phi_{ {\rm x} i}- \sum \limits_{i=1}^Z \phi_{ {\rm o} i}\hspace{0.2cm}{\rm mit} \hspace{0.2cm} \phi_K = \left\{ \begin{array}{c} 0 \\ \pi \end{array} \right. \begin{array}{c} {\rm{f\ddot{u}r} } \\ {\rm{f\ddot{u}r} } \end{array}\begin{array}{*{20}c} { K > 0\hspace{0.05cm},} \\ { K <0\hspace{0.05cm}.} \end{array}$$
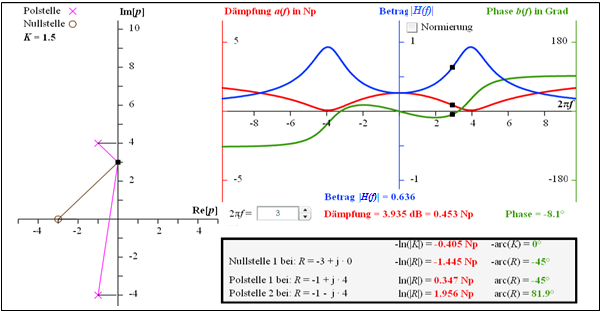
Die Grafik verdeutlicht die Berechnung der Dämpfungsfunktion $a(f)$ und der Phasenfunktion $b(f)$ eines Vierpols, der durch den Faktor $K =$ 1.5, eine Nullstelle bei –3 und zwei Pole bei –1 $±$j · 4 festliegt. Die angegebenen Zahlenwerte gelten für die Frequenz $2πf = 3$: $$a(f = \frac{3}{2\pi}) = 0.453\,\,{\rm Np}= 3.953\,\,{\rm dB} \hspace{0.2cm}\Rightarrow \hspace{0.2cm}|H(\frac{3}{2\pi})| = 0.636, b(\frac{3}{2\pi}) = -8.1 \,\,^\circ \hspace{0.05cm} .$$
Die Grafik ist ein Bildschirmabzug des Interaktionsmoduls
$$\href{https://intern.lntwww.de/cgi-bin/extern/uni.pl?uno=hyperlink&due=block&b_id=2294&hyperlink_typ=block_verweis&hyperlink_fenstergroesse=blockverweis_gross&session_id=}{ {\rm Kausale Systeme –Laplace–Transformation} }$$
Die Dämpfung $a(f)$ ist rot dargestellt und die Phase grün. Die Herleitung dieser Zahlenwerte ist im grau hinterlegten Block verdeutlicht. Für $|H(f)|$ ergibt sich ein bandpassähnlicher Verlauf (blaue Kurve) mit $$|H(f = 0)| \approx 0.25, \hspace{0.2cm} |H(f = \frac{4}{2\pi})| \approx 0637,\hspace{0.2cm} |H(f \rightarrow \infty)|= 0 \hspace{0.05cm} .$$