Exercise 3.1Z: Influence of the Message Phase in Phase Modulation

Zwei PM–Signalverläufe

Wir betrachten die Phasenmodulation verschiedener Schwingungen

$$ q(t) = \cos(\omega_{\rm N} \cdot t + \phi_{\rm N})\hspace{0.05cm}.$$

Das Quellensignal ist hierbei normiert (Amplitude $1$) dargestellt, so dass das phasenmodulierte Signal mit dem Modulationsindex (bzw. Phasenhub) $η$ wie folgt beschrieben werden kann:

$$s(t) = A_{\rm T} \cdot \cos \left(\omega_{\rm T} \cdot t + \eta \cdot q(t) \right)\hspace{0.05cm}.$$

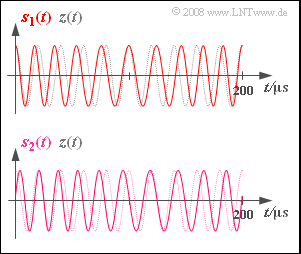
Das in der oberen Grafik dargestellte Signal $s_1(t)$ ist durch die Parameterwerte $ϕ_{\rm N} = -90^\circ$ und $η_1 = 2$ charakterisiert. Die Frequenz $f_{\rm N}$ dieses sinusförmigen Quellensignals soll ebenso wie die Trägerfrequenz $f_{\rm T}$ aus dem dargestellten Signalausschnitt der Dauer $200 \ \rm μs$ ermittelt werden.

Das Signal $s_2(t)$ unterscheidet sich von $s_1(t)$ möglicherweise durch eine andere Nachrichtenphase $ϕ_{\rm N}$ und einen anderen Modulationsindex $η$. Alle anderen Systemparameter sind gegenüber $s_1(t)$ unverändert.

Hinweise:

Die Aufgabe gehört zum Kapitel Phasenmodulation.
Bezug genommen wird insbesondere auf die Seite Signalverläufe bei Phasenmodulation.
Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

$f_{\rm N} \ = \ $

$\ \rm kHz$

$f_{\rm T} \ = \ $

$\ \rm kHz$

$ϕ_{\rm max} \ = \ $

$\ \rm rad$

$Δt_{\rm max} \ = \ $

$\ \rm μs$

$η_2 \ = \ $

$ϕ_{\rm N2} \ = \ $

$\ \rm Grad$

Musterlösung

Solution

1. Man erkennt aus der Skizze, dass der dargestellte Signalausschnitt der Dauer $200 μs$ genau der Periodendauer des sinusförmigen Quellensignals entspricht. Daraus folgt $f_N = 5 kHz$. Zu den Zeitpunkten $t = 0$, $t = 100 μs$ und $t = 200 μs$ sind die Signale $z(t)$ und $s(t)$ phasensynchron. In der ersten Halbwelle von $q(t)$ kommen die Nulldurchgänge von $s(t)$ etwas früher als die des Trägersignals $z(t)$, was auf eine positive Phase hinweist. Dagegen ist im Bereich von 100 bis 200 μs die Phase $ϕ(t) < 0$.

2. Es gilt $f_T = 50 kHz$, da im dargestellten Signalausschnitt ($200 μs$) von $z(t)$ genau 10 Perioden abgezählt werden können.

3. Die maximale relative Phasenabweichung beträgt $ϕ_{max} = η_1/(2π) ≈ 0.318$.

4.Da die Periodendauer des Trägers $T_0 = 20 μs$ ist, erhält man $Δt_{max} = ϕ_{max} ·T0 ≈ 6.37 μs$.

5. Die maximale Phasenabweichung (Verschiebung der Nulldurchgänge) ist bei $s_2(t)$ genau so groß wie bei $s_1(t)$. Daraus kann auf $η_2 = η_1 = 2$ geschlossen werden.

6.Das Signal $s_2(t)$ ist gegenüber $s_1(t)$ um $25 μs$ nach rechts verschoben. Deshalb muss auch für die Quellensignale gelten: $$ q_2(t) = q_1(t - 25\,{\rm \mu s}) = \cos(2 \pi f_{\rm N} (t - 25\,{\rm \mu s}) ) = \cos (\omega_{\rm N} \cdot t - 0.75 \cdot \pi)\hspace{0.05cm}.$$ Dies entspricht der Phasenlage $ϕ_{N2} = –135°$.