Exercise 4.11Z: OOK and BPSK once again

• Return to book

Fehlerwahrscheinlichkeiten von OOK und BPSK

Hier werden die Fehlerwahrscheinlichkeiten $p_{\rm S}$ von den digitalen Modulationsverfahren OOK und BPSK ohne Herleitung angegeben. Beispielsweise erhält man mit der sogenannten Q–Funktion

$$\rm Q (\it x) = \frac{\rm 1}{\sqrt{\rm 2\pi}}\cdot \int_{\it x}^{+\infty}\rm e^{\it -u^{\rm 2}/\rm 2}\,d \it u$$

für den AWGN–Kanal – gekennzeichnet durch $E_{\rm S}/N_0$ – und weiteren optimalen Voraussetzungen (zum Beispiel kohärente Demodulation)

• für On–Off–Keying (OOK), oft auch Amplitude Shift Keying (2–ASK) genannt:

$$p_{\rm S} = {\rm Q}\left ( \sqrt{{E_{\rm S}}/{N_0 }} \hspace{0.1cm}\right ) \hspace{0.05cm},$$

• und für Binary Phase Shift Keying (BPSK):

$$p_{\rm S} = {\rm Q}\left ( \sqrt{{2 \cdot E_{\rm S}}/{N_0 }} \hspace{0.1cm}\right ) \hspace{0.05cm}.$$

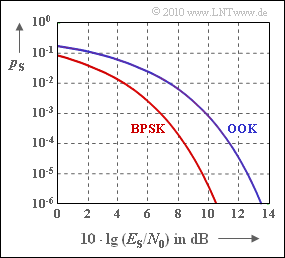
Diese Fehlerwahrscheinlichkeiten sind in der Grafik dargestellt. Für $10 \cdot {\rm lg} \, E_{\rm S}/N_0 = 10 \ \rm dB$ erhält man beispielsweise entsprechend den exakten Funktionen:

$$p_{\rm S} = 7.83 \cdot 10^{-4}\,\,{\rm (OOK)}\hspace{0.05cm},\hspace{0.3cm} p_{\rm S} = 3.87 \cdot 10^{-6}\,\,{\rm (BPSK)}\hspace{0.05cm}.$$

Um bei BPSK $p_{\rm S} = 10^{\rm –5}$ zu erreichen, muss $10 \cdot {\rm lg} \, E_{\rm S}/N_0 ≥ 9.6 \ \rm dB$ sein.

Hinweise:

• Die Aufgabe gehört zum Kapitel Trägerfrequenzsysteme mit kohärenter Demodulation des vorliegenden Buches.
• Die Herleitungen finden Sie auch im Kapitel Lineare digitale Modulation – Kohärente Demodulation.
• Für die numerischen Auswertungen können Sie die folgende obere Schranke verwenden:

$${\rm Q}(x) \le \frac{1}{\sqrt{2\pi} \cdot x} \cdot {\rm e}^{-x^2/2} \hspace{0.05cm}.$$

Fragebogen

1

Berechnen Sie die OOK–Bitfehlerwahrscheinlichkeit für $10 \cdot {\rm lg} \, E_{\rm S}/N_0 = 10 \ \rm dB$ unter Verwendung der oberen Schranke.

${\rm OOK}, \ 10 \cdot {\rm lg} \, E_{\rm S}/N_0 = 10 \ {\rm dB} \text{:} \hspace{0.2cm} p_{\rm S}$ = $\ \cdot 10^{\rm –4}$

2

Wie groß ist die BPSK–Bitfehlerwahrscheinlichkeit für $10 \cdot {\rm lg} \, E_{\rm S}/N_0 = 10 \ \rm dB$?

${\rm BPSK}, \ 10 \cdot {\rm lg} \, E_{\rm S}/N_0 = 10 {\rm dB} \text{:} \hspace{0.2cm} p_{\rm S}$ = $\ \cdot 10^{\rm –6}$

3

Geben Sie für On–Off–Keying den minimalen Wert für $E_{\rm S}/N_0$ (in $\rm dB$) an, damit gerade noch die Fehlerwahrscheinlichkeit $p_{\rm S} = 10^{\rm –5}$ erreicht wird.

${\rm OOK} \text{:} \hspace{0.2cm} 10 \cdot {\rm lg} \, E_{\rm S}/N_0$ = $\ \rm dB$

Musterlösung

Solution

(1)  Aus $10 \cdot {\rm lg} \, E_{\rm S}/N_0 = 10 \ \rm dB$ folgt $E_{\rm S}/N_0 = 10$ und damit

$$p_{\rm S} = {\rm Q}\left ( \sqrt{10} \right ) \approx \frac{\rm 1}{\sqrt{\rm 20\pi} }\cdot \rm e^{-5 } \underline{=8.5 \cdot 10^{-4}}\hspace{0.05cm}.$$

Der tatsächliche Wert gemäß dem Angabenblatt lautet $7.83 \cdot 10^{\rm –4}$. Die angegebene Gleichung ist also tatsächlich eine obere Schranke für ${\rm Q}(x)$. Der relative Fehler bei Verwendung dieser Näherung anstelle der exakten Funktion ${\rm Q}(x)$ ist in diesem Fall kleiner als $10\%$.

(2)  Bei BPSK lautet die entsprechende Gleichung:

$$p_{\rm S} = {\rm Q}\left ( \sqrt{20} \right ) \approx \frac{\rm 1}{\sqrt{\rm 40\pi} }\cdot \rm e^{-10 } \underline{=4.05 \cdot 10^{-6}}\hspace{0.05cm}.$$

Nun beträgt der relative Fehler bei Verwendung der Näherung nur noch $5\%$. Allgemein gilt: Je kleiner die Fehlerwahrscheinlichkeit ist, um so besser ist die Näherung.

(3)  Bei BPSK ist hierfür laut Angabe ein (logarithmierter) Wert von $9.6 \ \rm dB$ erforderlich. Bei der OOK muss der logarithmierte Wert um etwa $3 \ \rm dB$ erhöht werden ⇒ $10 \cdot {\rm lg} \, E_{\rm S}/N_{\rm 0 \ \underline {\approx 12.6 \ \rm dB}}$.