Exercise 2.4: GF(2 to the Power of 2) Representation Forms

${\rm GF}(2^2)$ in drei verschiedenen Darstellungen

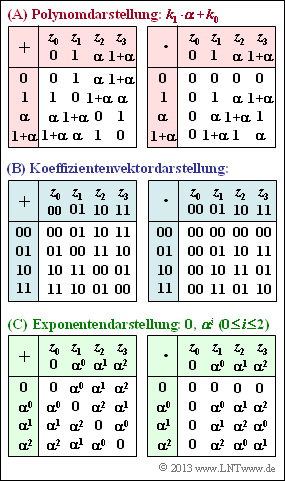
Nebenstehend sehen Sie für den Erweiterungskörper $\rm GF(2^2)$ die Additions– sowie die Multiplikationstabelle in drei verschiedenen Varianten:

die Polynomdarstellung,
die Koeffizientenvektordarstellung,
die Exponentendarstellung.

Hinweise:

Die Aufgabe bezieht sich auf das Kapitel Erweiterungskörper.
Alle notwendigen Informationen zu ${\rm GF}(2^2)$ finden Sie auf der Seite 1 dieses Kapitels.

Fragebogen

Musterlösung

Solution

(1) Zutreffend sind die Lösungsvorschläge 1, 2 und 5. Begründung:

Wäre $\alpha = 0$ oder $\alpha = 1$, so wäre das Pseudoelement $\alpha$ nicht mehr unterscheidbar von den beiden anderen ${\rm GF}(2)$–Elementen $0$ und $1$.
Die Modulo–$2$–Rechnung erkennt man aus der Additionstabelle. Beispielsweise gilt $1 + 1 = 0, \ \alpha + \alpha = 0, \ (1 + \alpha) + (1 + \alpha) = 0$, usw.
Aus der Multiplikationstabelle geht hervor, dass $\alpha^2 = \alpha \cdot \alpha = 1 + \alpha$ gilt (3. Zeile, 3. Spalte). Daraus lässt sich die Bedingung $\alpha^2 + \alpha + 1 = 0$ ablesen.

(2) Richtig ist Lösungsvorschlag 2. So steht „$01$” für das Element „$1$” und „$10$” für das Element „$\alpha$”.

(3) Richtig sind die Lösungsvorschläge 2 und 3. Es gilt $\alpha^0 = 1$ und $\alpha^1 = \alpha$. Bei dem zugrundeliegenden Polynom $p(x) = x^2 + x + 1$ folgt aus $p(\alpha) = 0$ weiterhin:

$$\alpha^2 +\alpha + 1 = 0 \hspace{0.3cm} \Rightarrow\hspace{0.3cm} \alpha^2 =\alpha + 1 \hspace{0.05cm}.$$

(4) Entsprechend den Tabellen der Polynomdarstellung gilt:

$$A \hspace{-0.15cm} \ = \ \hspace{-0.15cm} z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3 = $$

$$\hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha \cdot \alpha + \alpha \cdot (1+\alpha) + (1+\alpha) \cdot (1+\alpha) = (1+\alpha) + (1) + (\alpha) = 0 = z_0 \hspace{0.05cm},$$

$$ B \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (z_0 + z_1 + z_2) \cdot (z_0 + z_1 + z_3) = $$

$$\hspace{-0.15cm} \ = \ \hspace{-0.15cm} (0 + 1 + \alpha) \cdot (0 + 1 + 1+ \alpha) = (1+\alpha) \cdot \alpha = 1 = z_1 \hspace{0.05cm}.$$

Richtig sind demnach die Lösungsvorschläge 1 und 2. Zu den gleichen Ergebnissen kommt man mit der Koeffizientenvektordarstellung:

$$A \hspace{-0.15cm} \ = \ \hspace{-0.15cm} z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3 = $$

$$\hspace{-0.15cm} \ = \ \hspace{-0.15cm} (10) \cdot (10) + (10) \cdot (11) + (11) \cdot (11) = (11) + (01) + (10) = (00) = 0 = z_0 \hspace{0.05cm},$$

$$B \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (z_0 + z_1 + z_2) \cdot (z_0 + z_1 + z_3) = $$

$$\hspace{-0.15cm} \ = \ \hspace{-0.15cm} [(00) + (01) + (10)] \cdot [(00) + (01) + (11)] =(11) \cdot (10) = (01) = z_1 \hspace{0.05cm}.$$

Und schließlich mit der Exponentendarstellung:

$$A \hspace{-0.15cm} \ = \ \hspace{-0.15cm} z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3 = $$

$$\hspace{-0.15cm} \ = \ \hspace{-0.15cm} \alpha^1 \cdot \alpha^1 + \alpha^1 \cdot \alpha^2 + \alpha^2 \cdot \alpha^2 = \alpha^2 + \alpha^3 + \alpha^4 = \alpha^2 + \alpha^0 + \alpha^1 = 0 = z_0 \hspace{0.05cm},$$

$$B \hspace{-0.15cm} \ = \ \hspace{-0.15cm}(z_0 + z_1 + z_2) \cdot (z_0 + z_1 + z_3) = $$

$$\hspace{-0.15cm} \ = \ \hspace{-0.15cm} [0 + \alpha^0 + \alpha^1] \cdot [0 + \alpha^0 + \alpha^2] = \alpha^2 \cdot \alpha^1 = \alpha^3 = \alpha^0 = z_1 \hspace{0.05cm}.$$

	Die Elemente $\alpha$ und $1 + \alpha$ sind weder $0$ noch $1$.
	Die Rechenoperationen erfolgen modulo $2$.
	Die Rechenoperationen erfolgen modulo $4$.
	Man erkennt „$\alpha^2 + \alpha + 1 = 0$” aus der Additionstabelle.
	Man erkennt „$\alpha^2 + \alpha + 1 = 0$” aus der Multiplikationstabelle.

	Es sind keine Zusammenhänge erkennbar.
	Die Elemente $0, \ 1$ und $\alpha$ sind in beiden Darstellungen gleich.
	Das Element $1 + \alpha$ lautet in der Exponentendarstellung $\alpha^2$.
	Das Element $\alpha^2$ der Exponentendarstellung steht für $\alpha \cdot (1 + \alpha)$.

	Es gilt $A = z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3 = z_0$,
	Es gilt $B = (z_0 + z_1 + z_2) \cdot (z_0 + z_1 + z_3) = z_1$,
	Es gilt $A = z_2 \cdot z_2 + z_2 \cdot z_3 + z_3 \cdot z_3 = z_2$,
	Es gilt $B = (z_0 + z_1 + z_2) \cdot (z_0 + z_1 + z_3) = z_3$.

	$(k_0 \ k_1)$ bezieht sich auf das Element $k_1 \cdot \alpha + k_0$.
	$(k_1 \ k_0)$ bezieht sich auf das Element $k_1 \cdot \alpha + k_0$.
	Zwischen beiden Darstellungen besteht keinerlei Zusammenhang.