Exercise 2.6: GF(P power m). Which P, which m?

• Return to book

Additions– und Multiplikationstabelle

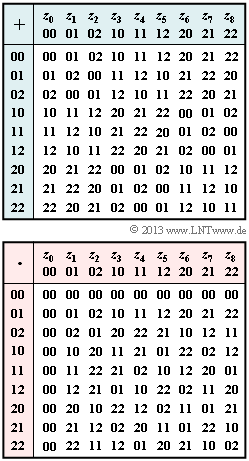
Es soll ein Galoisfeld ${\rm GF}(q)$ mit $q = P^m$ Elementen analysiert werden, das durch die nebenstehenden Tabellen für Addition (gekennzeichnet mit „$+$”) und Multiplikation (gekennzeichnet mit „$\cdot$”) vorgegeben ist. Dieses Galoisfeld

$${\rm GF}(q) = \{\hspace{0.1cm}z_0,\hspace{0.1cm} z_1,\hspace{0.1cm} ... , \hspace{0.1cm}z_{q-1}\}$$

erfüllt alle Anforderungen an einen endlichen Körper, die im Kapitel 2.1 aufgeführt sind. Kommutativ–, Assoziativ– und Distributivgesetz werden erfüllt. Weiterhin gibt es

• ein neutrales Element hinsichtlich Addition  ⇒  $N_{\rm A}$:

$$\exists \hspace{0.15cm} z_j \in {\rm GF}(q) : \hspace{0.25cm}z_i + z_j = z_i $$

$$\hspace{0.25cm} \Rightarrow \hspace{0.25cm} z_j = N_{\rm A} = {\rm "0"} \hspace{0.25cm}{\rm (Nullelement)} \hspace{0.05cm},$$

• ein neutrales Element hinsichtlich Multiplikation  ⇒  $N_{\rm M}$:

$$\exists \hspace{0.15cm} z_j \in {\rm GF}(q) : \hspace{0.25cm}z_i \cdot z_j = z_i $$

$$ \Rightarrow \hspace{0.25cm} z_j = N_{\rm M} = {\rm "1"} \hspace{0.25cm}{\rm (Einselement)} \hspace{0.05cm},$$

• für alle Elemente $z_i$ eine additive Inverse  ⇒  ${\rm Inv_A}(z_i)$:

$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q)\hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_A}(z_i) \in {\rm GF}(q):$$

$$z_i + {\rm Inv_A}(z_i) = N_{\rm A} = {\rm "0"}\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm kurz:}\hspace{0.15cm} {\rm Inv_A}(z_i) = - z_i \hspace{0.05cm}, $$

• für alle Elemente $z_i$ mit Ausnahme des Nullelements eine multiplikative Inverse  ⇒  ${\rm Inv_M}(z_i)$:

$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} z_i \ne N_{\rm A} \hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_M}(z_i) \in {\rm GF}(q):$$

$$z_i \cdot {\rm Inv_M}(z_i) = N_{\rm M} = {\rm "1"} \hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm kurz:}\hspace{0.15cm} {\rm Inv_M}(z_i) = z_i^{-1} \hspace{0.05cm}. $$

Hinweise:

• Die Aufgabe bezieht sich auf das Kapitel Erweiterungskörper.
• In den Tabellen sind die Elemente $z_0, \ ... \ , \ z_8$ als Koeffizientenvektoren bezeichnet. So steht zum Beispiel „$21$” für die ausführliche Schreibweise $2 \cdot \alpha + 1$.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Geben Sie die Parameter des hier betrachteten Galoisfeldes an.

$P \ = \ $

$m \ = \ $

$q \ = \ $

2

Wie lautet das neutrale Element für die Addition?

	Das neutrale Element der Addition ist $N_{\rm A} = „00”$,
	Das neutrale Element der Addition ist $N_{\rm A} = „01”$.

3

Wie lautet das neutrale Element für die Multiplikation?

	Das neutrale Element der Multiplikation ist $N_{\rm M} = „00”$,
	Das neutrale Element der Multiplikation ist $N_{\rm M} = „01”$.

4

Welche Aussagen gelten hinsichtlich der additiven Inversen?

	Es gilt ${\rm Inv_A} \, („02”) = „01”$,
	Es gilt ${\rm Inv_A} \, („11”) = „22”$,
	Es gilt ${\rm Inv_A} \, („22”) = „00”$.

5

Welche der folgenden Aussagen treffen für die Multiplikation zu?

	Die Multiplikation erfolgt modulo $p(\alpha) = \alpha^2 + 2$.
	Die Multiplikation erfolgt modulo $p(\alpha) = \alpha^2 + 2\alpha + 2$.

6

Welche Aussagen gelten hinsichtlich der multiplikativen Inversen?

	Es gibt für alle Elemente $z_i ∈ {\rm GF}(P^m)$ eine multiplikative Inverse.
	Es gilt ${\rm Inv_M}(„12”) = „10”$.
	Es gilt ${\rm Inv_M}(„21”) = „12”$.

7

Gilt $(„20” + „12”) \cdot („12”) = „20” \cdot „12” + „12” \cdot „12”$?

	Ja,
	Nein.

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)