Exercise 2.10: Reed-Solomon Error Detection

• Return to book

Distanzspektren zweier verschiedener Reed–Solomon–Codes

Bei einem linearen Blockcode können bis zu $e = d_{\rm min} - 1$ Fehler erkannt werden. Bei allen Reed–Solomon–Codes beträgt dabei die minimale Distanz

$$d_{\rm min} = n-k+1 \hspace{0.05cm}.$$

Man muss folgende Fälle unterscheiden:

• Treten nicht mehr als $e = n - k$ Symbolfehler auf, so wird der Block als fehlerhaft erkannt.
• Die Fehlererkennung kann auch bei mehr als $n - k$ Symbolfehlern noch funktionieren, und zwar dann, wenn das Empfangswort kein gültiges Codewort des Reed–Solomon–Codes ist:

$$\underline {y} \notin C_{\rm RS} = \{ \underline {c}_{\hspace{0.05cm}0}, \hspace{0.05cm}\text{...} \hspace{0.1cm}, \underline {c}_i, \hspace{0.05cm}\text{...} \hspace{0.1cm}, \underline {c}_{\hspace{0.05cm}n -1} \} \hspace{0.05cm}.$$

• Ist aber das verfälschte Empfangswort $(\underline{y} ≠ \underline{c})$ ein gültiges Codewort  ⇒  $\underline{y}$, so bleibt bei der Decodierung der fehlerhafte Block unentdeckt. Wir definieren als Blockfehlerwahrscheinlichkeit.

$${\rm Pr}({\rm Blockfehler}) = {\rm Pr}(\underline {y} \ne \underline {c}) \hspace{0.05cm}.$$

In dieser Aufgabe soll diese Wahrscheinlichkeit für folgende Codes ermittelt werden:

• Reed–Solomon–Code $(7, \, 3, \, 5)_8 \ \Rightarrow \ d_{\rm min} = 5$,
• Reed–Solomon–Code $(7, \, 5, \, 3)_8 \ \Rightarrow \ d_{\rm min} = 3$.

Weiterhin soll gelten:

• Jedes Symbol wird mit der Wahrscheinlichkeit $\varepsilon_{\rm S} = 0.1$ in ein anderes Symbol verfälscht und mit der Wahrscheinlichkeit $1 - \varepsilon_{\rm S} = 0.9$ richtig übertragen.
• Für das Distanzspektrum eines Reed–Solomon–Codes der Länge $n$ gilt mit $d = d_{\rm min}$:

$$W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \big [\hspace{0.03cm}q^{i\hspace{0.03cm}-\hspace{0.03cm}j\hspace{0.03cm}-\hspace{0.03cm}d\hspace{0.03cm}+\hspace{0.03cm}1}-1 \hspace{0.03cm} \big ]\hspace{0.05cm}.$$

Daneben sollen zwei Schranken für die Blockfehlerwahrscheinlichkeit betrachtet und bewertet werden:

• Ist allein die minimale Distanz bekannt, so kann man daraus eine obere Schranke ableiten. Die Gewichtsfaktoren $W_i$ sind dabei so zu wählen, dass sicher (das heißt: bei allen Konstellationen) gilt:

$${\rm Pr}({\rm Obere\hspace{0.15cm} Schranke}) \ge {\rm Pr}({\rm Blockfehler}) \hspace{0.05cm}.$$

• Eine untere Schranke erfordert zusätzlich die Kenntnis der Gewichtsfunktion $W_i$ für $i = d_{\rm min}$. Damit kann folgende Bedingung erfüllt werden:

$${\rm Pr}({\rm Untere\hspace{0.15cm} Schranke}) \le {\rm Pr}({\rm Blockfehler}) \hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Definition und Eigenschaften von Reed–Solomon–Codes.
• Bezug genommen wird insbesondere auf die Seite Singleton–Schranke und minimale Distanz.
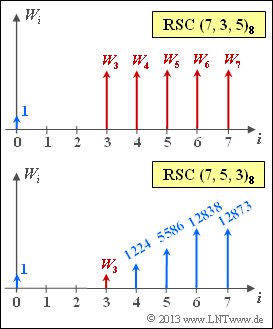
• Zu berechnen sind die in der obigen Grafik rot markierten Gewichte $W_i$.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Berechnen Sie das Distanzspektrum für den $\rm RSC \, (7, \, 3, \, 5)_8$.

$W_3 \ = \ $

$W_4 \ = \ $

$W_5 \ = \ $

$W_6 \ = \ $

$W_7 \ = \ $

2

Wie lautet das in der Grafik fehlende Gewicht des $\rm RSC \, (7, \, 5, \, 3)_8$?

$W_3 \ = \ $

3

Mit welcher Wahrscheinlichkeit bleibt ein fehlerhafter Block unerkannt? Die Verfälschungswahrscheinlichkeit eines Symbols sei $\varepsilon = 0.1$.

$\rm RSC \, (7, \, 3, \, 5) \text{:} \hspace{0.4cm} Pr(Blockfehler) \ = \ $ $\ \cdot 10^{-5}$

$\rm RSC \, (7, \, 5, \, 3) \text{:} \hspace{0.4cm} Pr(Blockfehler) \ = \ $ $\ \cdot 10^{-5}$

4

Berechnen und bewerten Sie für beide Codes die in der Angabe vorgeschlagene obere Schranke $p_{\rm oben} = \rm Pr(Obere \ Schranke)$.

${\rm RSC} \, (7, \, 3, \, 5) \text{:} \hspace{0.4cm} p_{\rm oben} \ = \ $ $\ \cdot 10^{-5}$

${\rm RSC} \, (7, \, 5, \, 3) \text{:} \hspace{0.4cm} p_{\rm oben} \ = \ $ $\ \cdot 10^{-5}$

5

Berechnen und bewerten Sie für beide Codes die in der Angabe vorgeschlagene untere Schranke $p_{\rm unten} = \rm Pr(Untere \ Schranke)$.

${\rm RSC} \, (7, \, 3, \, 5) \text{:} \hspace{0.4cm} p_{\rm unten} \ = \ $ $\ \cdot 10^{-5}$

${\rm RSC} \, (7, \, 5, \, 3) \text{:} \hspace{0.4cm} p_{\rm unten} \ = \ $ $\ \cdot 10^{-5}$

Musterlösung

Solution

(1)  Die Gleichung zur Beschreibung der Gewichte $W_i$ lautet (die minimale Distanz $d_{\rm min}$ ist hier mit $d$ abgekürzt):

$$W_i = {n \choose i} \cdot \sum_{j = 0}^{i-d}\hspace{0.15cm}(-1)^j \cdot {i \choose j} \cdot \big [\hspace{0.03cm}q^{i\hspace{0.03cm}-\hspace{0.03cm}j\hspace{0.03cm}-\hspace{0.03cm}d\hspace{0.03cm}+\hspace{0.03cm}1}-1 \hspace{0.03cm} \big ]\hspace{0.05cm}.$$

Wegen der minimalen Distanz $d_{\min} = 5$ sind $W_3 \ \underline{= 0}$ und $W_4 \ \underline{= 0}$. Die weiteren Gewichte ergeben sich zu

$$W_5 = {7 \choose 5} \cdot (8^1 - 1) = \frac {7 \cdot 6 \cdot 5 \cdot4 \cdot 3}{1 \cdot 2 \cdot 3 \cdot4 \cdot 5} \cdot 7 = 21 \cdot 7 \hspace{0.15cm}\underline {= 147}\hspace{0.05cm},$$

$$W_6 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {7 \choose 6} \cdot \sum_{j = 0}^{1}\hspace{0.15cm}(-1)^j \cdot {6 \choose j} \cdot \big (\hspace{0.03cm}8^{2\hspace{0.03cm}-\hspace{0.03cm}j} -1 \big )=7 \cdot \left [ (8^2 - 1) - 6 \cdot (8^1 - 1)\right ] = 7 \cdot (63-42) \hspace{0.15cm}\underline {= 147}\hspace{0.05cm},$$

$$W_7 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {7 \choose 7} \cdot \sum_{j = 0}^{2}\hspace{0.15cm}(-1)^j \cdot {7 \choose j} \cdot \big (\hspace{0.03cm}8^{3\hspace{0.03cm}-\hspace{0.03cm}j} -1 \big )= (8^3 - 1) - 7 \cdot (8^2 - 1) +21 \cdot (8^1 - 1) = 511 - 7 \cdot 63 + 21 \cdot 7 \hspace{0.15cm}\underline {= 217}\hspace{0.05cm},$$

$$\Rightarrow \hspace{0.3cm}W_0 + W_5 + W_6 + W_7 = 1 + 147 + 147 + 217 = 512 = 8^3 = q^k\hspace{0.05cm}.$$

(2)  Analog zur Teilaufgabe (1) erhält man:

$$W_3 = {7 \choose 3} \cdot (8^1 - 1) = \frac {7 \cdot 6 \cdot 5 }{1 \cdot 2 \cdot 3 } \cdot 7 = 35 \cdot 7 \hspace{0.15cm}\underline {= 245}\hspace{0.05cm}.$$

(3)  Die Verfälschungswahrscheinlichkeit eines einzelnen Symbols ist mit $\varepsilon_{\rm S} = 0.1$ gegeben. Dann gilt für die Wahrscheinlichkeit, dass in einem Codewort mit $n = 7$ Codesymbolen

• genau 3 Symbole verfälscht werden:

$$p_3 = 0.1^3 \cdot 0.9^4 = 0.6561 \cdot 10^{-3} \hspace{0.05cm},$$

• genau 4 Symbole verfälscht werden:

$$p_4 = 0.1^4 \cdot 0.9^3 = 0.729 \cdot 10^{-4} \hspace{0.05cm},$$

• genau 5 Symbole verfälscht werden:

$$p_5 = 0.1^5 \cdot 0.9^2 = 0.81 \cdot 10^{-5} \hspace{0.05cm},$$

• genau 6 Symbole verfälscht werden:

$$p_6 = 0.1^6 \cdot 0.9 = 0.9 \cdot 10^{-6}\hspace{0.05cm},$$

• alle $n = 7$ Symbole verfälscht werden:

$$p_7 = 0.1^7 = 10^{-7}\hspace{0.05cm}.$$

Beim $\rm RSC \, (7, \, 3, \, 5)_8$ kann das Nullwort durch Symbolfehler in eines von $q^k - 1 = 8^3 - 1 = 511$ anderen Codeworten verfälscht werden. Damit erhält man mit den Gewichtsfunktionen von Teilaufgabe (1):

$${\rm Pr}({\rm Blockfehler}) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \frac {W_5 \cdot p_5 + W_6 \cdot p_6 + W_7 \cdot p_7}{511} =\frac {147 \cdot 0.81 \cdot 10^{-5} + 147 \cdot 0.9 \cdot 10^{-6} + 217 \cdot 10^{-7}}{511} \hspace{0.15cm}\underline {\approx 0.263 \cdot 10^{-5}} \hspace{0.05cm}.$$

Beim $\rm RSC \, (7, \, 5, \, 3)_8$ muss wegen $k = 5$ über $8^5 - 1 = 32767$ Verfälschungswahrscheinlichkeiten gemittelt werden. Mit $W_3 = 245$ aus Teilaufgabe (2) und den Gewichten $W_4 = 1224, \ W_5 = 5586, \ W_6 = 12838, \ W_7 = 12873$ entsprechend dem Angabenblatt erhält man hierfür:

$${\rm Pr}({\rm Blockfehler}) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \frac {W_3 \cdot p_3 + W_4 \cdot p_4 + W_5 \cdot p_5 + W_6 \cdot p_6 + W_7 \cdot p_7}{32767} =\frac {245 \cdot 0.656 \cdot 10^{-3} + \hspace{0.15cm}... \hspace{0.15cm}+ 12873 \cdot 10^{-7}}{32767} \hspace{0.15cm}\underline {\approx 0.942 \cdot 10^{-5}} \hspace{0.05cm}.$$

(4)  Bekannt sei nur $d_{\rm min}$ (weiter mit $d$ abgekürzt) und damit auch $p_d = \epsilon_{\rm S}^d \cdot (1 - \epsilon_{\rm S})^{n-d}$. Dies ist gleichzeitig die gesuchte obere Schranke:

• ${\rm RSC} \, (7, \, 3, \, 5)_8 \text{:} \hspace{0.33cm} {\rm Pr(Obere \ Schranke)} = p_5 = \underline{0.81 \cdot 10^{-5}}$,
• ${\rm RSC} \, (7, \, 5, \, 3)_8 \text{:} \hspace{0.33cm} {\rm Pr(Obere \ Schranke)} = p_3 = \underline{65.6 \cdot 10^{-5}}$.

Da das Gewicht $W_d$ als nicht bekannt vorausgesetzt wurde, setzt man dieses auf den maximal möglichen Wert ($W_5 = 511$ bzw. $W_3 = 32767$), so dass die Vorfaktoren in den Gleichungen zur Teilaufgabe (3) verschwinden. Nur so ist eine obere Schranke sichergestellt.

Die obere Schranke liegt in beiden Fällen deutlich über den Ergebnissen der Teilaufgabe (3):

• $\rm RSC \, (7, \, 3, \, 5)_8 \text{:} \hspace{0.33cm} 0.810 \cdot 10^{-5}$ statt $0.263 \cdot 10^{-5}$ (Faktor ca. $3$),
• $\rm RSC \, (7, \, 5, \, 3)_8 \text{:} \hspace{0.33cm} 65.6 \cdot 10^{-5}$ statt $0.942 \cdot 10^{-5}$ (Faktor ca. $70$).

(5)  Mit der Abkürzung $d = d_{\rm min}$ erhält man für die untere Schranke:

$${\rm Pr}({\rm Untere\hspace{0.15cm} Schranke})= \frac{W_d \cdot p_d}{q^k -1} \hspace{0.05cm}.$$

• Für den $\rm RSC \, (7, \, 3, \, 5)_8$ liegt wegen $W_d = W_5$ und $p_d = p_5$ die unter Schranke um etwa $11\%$ unterhalb des tatsächlichen Wertes $(0.263 \cdot 10^{-5})$:

$${\rm Pr}({\rm Untere\hspace{0.15cm} Schranke}) = \frac{147 \cdot 0.81 \cdot 10^{-5}}{511} \hspace{0.15cm}\underline {\approx 0.233 \cdot 10^{-5}}$$

• Für den $\rm RSC \, (7, \, 5, \, 3)_8$ gilt mit $W_d = W_3$ und $p_d = p_3$ weicht die untere Schranke hier vom tatsächlichen Wert $(0.942 \cdot 10^{-5})$stärker ab, weil bei diesem Code die Beiträge der höheren Gewichte $(W_4, \ W_5, \ W_6, \ W_7)$ in Relation zu $W_3$ relevanter sind:

$${\rm Pr}({\rm Untere\hspace{0.15cm} Schranke}) = \frac{245 \cdot 0.656 \cdot 10^{-3}}{32767} \hspace{0.15cm}\underline {\approx 0.494 \cdot 10^{-5}}\hspace{0.05cm}.$$