Exercise 4.2Z: About the Sampling Theorem

• Return to book

Harmonische Schwingungen unterschiedlicher Phase

Das Abtasttheorem besagt, dass die Abtastfrequenz $f_{\rm A} = 1/T_{\rm A}$ mindestens doppelt so groß sein muss wie die größte im Quellensignal $q(t)$ enthaltene Frequenz $f_\text {N, max}$:

$$f_{\rm A} \ge 2 \cdot f_{\rm N,\hspace{0.05cm}max}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} T_{\rm A} \le \frac{1}{2 \cdot f_{\rm N, \hspace{0.05cm}max}}\hspace{0.05cm}.$$

Wird diese Bedingung erfüllt, so kann beim Empfänger das Nachrichtensignal durch einen rechteckförmigen (idealen) Tiefpass mit dem Frequenzgang

$$H(f) = \left\{ \begin{array}{l} 1 \\ 1/2 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < f_{\rm G},} \\ {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| = f_{\rm G},} \\ {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| > f_{\rm G}} \\ \end{array}$$

vollständig rekonstruiert werden, das heißt, es gilt dann $v(t) = q(t)$.

• Die Grenzfrequenz $f_{\rm G}$ ist dabei gleich der halben Abtastfrequenz zu wählen.
• Das Gleichheitszeichen gilt allgemein nur dann, wenn das Spektrum $Q(f)$ keine diskrete Spektrallinie bei der Frequenz $f_\text {N, max}$ beinhaltet.

In dieser Aufgabe werden drei verschiedene Quellensignale betrachtet, die sich jeweils als harmonische Schwingung

$$q(t) = A \cdot \cos (2 \pi \cdot f_{\rm N} \cdot t - \varphi)$$

mit der Amplitude $A = 1\ \rm V$ und der Frequenz $f_{\rm N}= 5 \ \rm kHz$ darstellen lassen. Für die Spektralfunktion $Q(f)$ aller dargestellten Zeitsignale gilt allgemein:

$$Q(f) = \frac{A}{2} \cdot \delta (f- f_{\rm N}) \cdot {\rm e}^{-{\rm j}\hspace{0.04cm}\cdot \hspace{0.04cm}\varphi}+ \frac{A}{2} \cdot \delta (f+ f_{\rm N}) \cdot {\rm e}^{+{\rm j}\hspace{0.04cm}\cdot \hspace{0.04cm}\varphi}\hspace{0.05cm}.$$

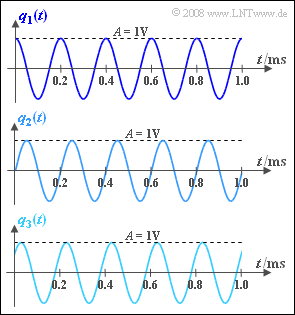
Die in der Grafik skizzierten Schwingungen unterscheiden sich allein durch die Phase $φ$:

• $φ_1 = 0$   ⇒   Cosinussignal $q_1(t)$,
• $φ_2 = π/2 \ (= 90^\circ)$   ⇒   Sinussignal $q_2(t)$,
• $φ_3 = π/4 \ (= 45^\circ)$   ⇒   Signal $q_3(t)$.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Pulscodemodulation.
• Bezug genommen wird insbesondere auf die Seite  Abtastung und Signalrekonstruktion.
• Das abgetastete Quellensignal wird mit $q_{\rm A}(t)$ bezeichnet und dessen Spektralfunktion mit $Q_{\rm A}(f)$. Die Abtastung erfolgt stets bei $ν · T_{\rm A}$.

Fragebogen

1

Welche Aussagen gelten mit  $f_{\rm A} = 11\ \rm kHz$?

	Das Abtasttheorem wird stets erfüllt.
	Alle Signale können durch einen Tiefpass rekonstruiert werden.
	Es gilt stets  $Q_{\rm A}(f = 5 \ \rm kHz) = Q(f = 5 \ \rm kHz)$.

2

Welcher Abtastabstand ergibt sich mit  $f_{\rm A} = 10\ \rm kHz$?

$T_{\rm A} \ = \ $ $\ \rm ms$

3

Welche Aussagen gelten für das Signal  $q_1(t)$  und  $f_{\rm A} = 10\ \rm kHz$?

	Es gilt  $Q_{\rm A}(f = 5 \ {\rm kHz)} = Q_1(f = 5 \ \rm kHz)$.
	Eine vollständige Signalrekonstruktion ist möglich   ⇒   $v_1(t) = q_1(t)$.
	Das rekonstruierte Signal ist  $v_1(t) \equiv 0$.

4

Welche Aussagen gelten für das Signal  $q_2(t)$  und  $f_{\rm A} = 10\ \rm kHz$?

	Es gilt  $Q_{\rm A}(f = 5 \ {\rm kHz)} = Q_2(f = 5 \ \rm kHz)$.
	Eine vollständige Signalrekonstruktion ist möglich   ⇒   $v_2(t) = q_2(t)$.
	Das rekonstruierte Signal ist  $v_2(t) \equiv 0$.

5

Welche Aussagen gelten für das Signal  $q_3(t)$ und $f_{\rm A} = 10\ \rm kHz$?

	Es gilt  $Q_{\rm A}(f = 5 \ {\rm kHz)} = Q_3(f = 5 \ \rm kHz)$.
	Eine vollständige Signalrekonstruktion ist möglich   ⇒   $v_3(t) = q_3(t)$.
	Das rekonstruierte Signal ist  $v_3(t) \equiv 0$.

Musterlösung

Solution

(1)  Alle Aussagen sind zutreffend:

• Das Abtasttheorem wird mit $f_{\rm A} = 11 \ \rm kHz > 2 · 5 \ \rm kHz$ erfüllt, so dass eine vollständige Signalrekonstruktion immer möglich ist.
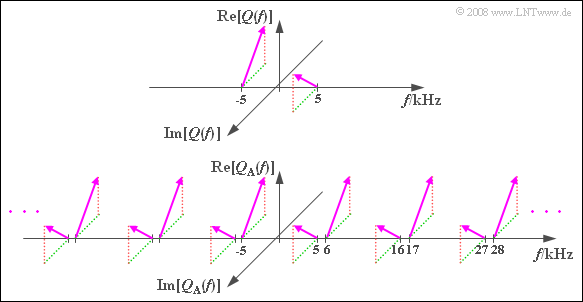
• Das Spektrum $Q_{\rm A}(f)$ ergibt sich aus $Q(f)$ durch periodische Fortsetzung im jeweiligen Frequenzabstand $f_{\rm A}$, was in der ersten Grafik am Beispiel der Spektralfunktion $Q_3(f)$ allgemein verdeutlicht wird.
• Durch einen rechteckförmigen Tiefpass mit Grenzfrequenz $f_{\rm G} = f_{\rm A}/2 = 5.5 \ \rm kHz$ erhält man das ursprüngliche Spektrum $Q(f)$.

Spektralfunktion des abgetasteten Signals

Die Verschiebung um

• $f_{\rm A} = 11 \ \rm kHz$ liefert Spektrallinien bei $+6 \ \rm kHz$ und $+16 \ \rm kHz$,
• $-f_{\rm A} = -11 \ \rm kHz$ liefert Spektrallinien bei $-6 \ \rm kHz$ und $-16 \ \rm kHz$,
• $2 · f_{\rm A} = 22 \ \rm kHz$ liefert Spektrallinien bei $+17 \ \rm kHz$ und $+27 \ \rm kHz$,
• $-2 · f_{\rm A}= -22 \ \rm kHz$ liefert Spektrallinien bei $-17 \ \rm kHz$ und $-27 \ \rm kHz$.

(2)  Der Abtastabstand ist gleich dem Kehrwert der Abtastfrequenz:

$$T_{\rm A} = {1}/{f_{\rm A} }\hspace{0.15cm}\underline { = 0.1\,{\rm ms}} \hspace{0.05cm}.$$

(3)  Richtig ist der Lösungsvorschlag 2:

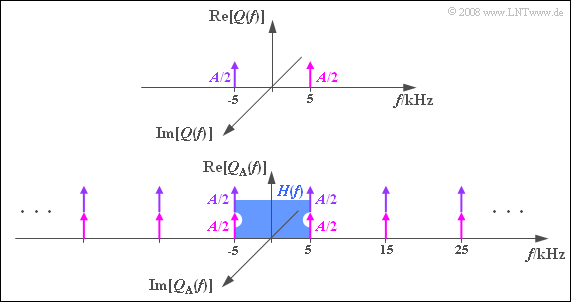
• Beim cosinusförmigen Signal ergibt sich entsprechend der nächsten Grafik mit $f_{\rm A} = 10 \ \rm kHz$ das Spektrum $Q_{\rm A}(f)$: Alle Spektrallinien sind reell.
• Die Periodifizierung von $Q(f)$ mit $f_{\rm A} = 10 \ \rm kHz$ führt zu einem Diracpuls mit Spektrallinien bei $±f_{\rm N}$, $±f_{\rm N}± f_{\rm A}$, $±f_{\rm N}± 2f_{\rm A}$, ...
• Durch die Überlagerungen haben alle Diracfunktionen das Gewicht $A$, während die beiden Spektrallinien von $Q(f)$ nur jeweils mit $A/2$ gewichtet sind.
• Wegen $H(f = f_{\rm N}) = H(f = f_{\rm G}) = 0.5$ ist das Spektrum $V_1(f)$ nach dem Tiefpass identisch mit $Q_1(f)$ und dementsprechend gilt auch $v_1(t) = q_1(t)$.
• Im Zeitbereich kann man sich die Signalrekonstruktion wie folgt vorstellen: Die Abtastwerte von $q_1(t)$ liegen genau bei den Signalmaxima und –minima. Der Tiefpass formt daraus das Cosinussignal mit richtiger Amplitude, Frequenz und Phase.

Spektralfunktion des abgetasteten Cosinussignals

Abgetastetes Sinussignal

(4)  Richtig ist der Lösungsvorschlag 2:

• Alle Abtastwerte von $q_2(t)$ liegen nun genau bei den Nulldurchgängen des Sinussignals, das heißt, dass hier $q_{\rm A}(t) \equiv 0$ gilt.
• Damit ergibt sich aber natürlich auch $v_2(t) \equiv 0$.
• Im Spektralbereich kann man das Ergebnis mit Hilfe der Grafik zur Teilaufgabe (1) herleiten. $Q(f)$ ist rein imaginär und die Imaginärteile bei $±f_{\rm N}$ haben unterschiedliche Vorzeichen. Somit heben sich bei der Periodifizierung jeweils ein positiver und ein negativer Anteil auf ⇒ $Q_{\rm A}(f) \equiv 0$   ⇒   $V_2(f) \equiv 0$.

Abgetastete harmonische Schwingung mit Phase $φ_3 = π/4$

(5)  Keiner der vorgegebenen Lösungsvorschlägen ist richtig:

• Ersetzt man in der Grafik zur Teilaufgabe (1) die Abtastfrequenz $f_{\rm A} = 11 \ \rm kHz$ durch $f_{\rm A} = 10 \ \rm kHz$, so addieren sich zwar die Realteile, aber die Imaginärteile löschen sich aus.
• Das heißt, dass nun $Q_{\rm A}(f)$ und $V_3(f)$ reelle Spektren sind. Das heißt weiter: Die Phaseninformation geht verloren ($φ = 0$) und das Ausgangssignal $v_3(t)$ ist ein Cosinussignal.
• Die Signale $q_3(t)$ und $v_3(t)$ unterscheiden sich somit sowohl in der Amplitude als auch in der Phase. Lediglich die Frequenz bleibt erhalten.

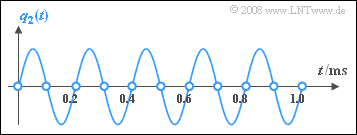
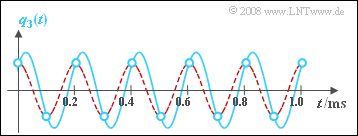
Die Grafik zeigt türkisfarben das Signal $q_3(t)$, dessen Abtastwerte (Kreise) sowie rot gestrichelt das Ausgangssignal $v_3(t)$ des Tiefpasses. Man erkennt, dass der Tiefpass genau das Ergebnis liefert, für das wahrscheinlich auch Sie sich entscheiden würden, wenn Sie durch die (roten) Abtastwerte einen Kurvenzug einzeichnen sollten.