Properties of Nyquist Systems

Erstes Nyquistkriterium im Zeitbereich

Für das gesamte erste Hauptkapitel wurde vorausgesetzt, dass die Detektion eines Symbols nicht durch Nachbarimpulse beeinträchtigt werden soll. Dies erreicht man durch die Detektion des Signals

$d(t) = \sum \limits_{\it (\nu)} a_\nu \cdot g_d ( t - \nu T)$

zu den Detektionszeitpunkten $(\nu \cdot T)$ immer dann, wenn der Detektionsgrundimpuls $g_d(t)$

auf den Bereich $|t| < T$ beschränkt ist, was für das letzte Kapitel Fehlerwahrscheinlichkeit bei Basisbandübertragung vorausgesetzt wurde, oder
äquidistante Nulldurchgänge zu den Detektionszeitpunkten $\nu \cdot T$ aufweist.

Aus Gründen einer möglichst einfachen Darstellung wird im Folgenden das Detektionsstörsignal als vernachlässigbar klein angenommen $(d_{\rm N}(t) =0)$ .

$\text{Definition:}$ Man bezeichnet einen Detektionsgrundimpuls mit den Eigenschaften

$g_d ( t = \nu T)= 0 \hspace{0.3cm}{\rm{f\ddot{u}r} }\hspace{0.3cm} \nu = \pm 1, \pm 2,\pm 3,\hspace{0.05cm}\text{...}$

als Nyquistimpuls $g_{\hspace{0.05cm}\rm Nyq}(t)$ , benannt nach dem Physiker Harry Nyquist.

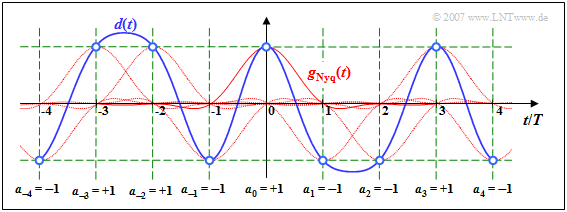
Detektionssignal bei Nyquistimpulsformung

$\text{Beispiel 1:}$ Die Grafik zeigt das Detektionssignal $d(t)$ eines solchen Nyquistsystems. Rot gepunktet sind die (gewichteten und verschobenen) Nyquistimpulse $a_\nu \cdot g_{\hspace{0.05cm}\rm Nyq}(t -\nu \cdot T)$ eingezeichnet.

Bitte beachten Sie:

Zu den Detektionszeitpunkten gilt $d(\nu \cdot T) = a_\nu \cdot g_{\hspace{0.05cm}\rm Nyq}(0)$ , wie aus den blauen Kreisen und dem grünen Raster hervorgeht.
Die Nachläufer der vorangegangenen Impulse $(\nu < 0)$ sowie die Vorläufer der nachfolgenden Impulse $(\nu > 0)$ beeinflussen beim Nyquistsystem die Detektion des Symbols $a_0$ nicht.

Der Vollständigkeit halber sei erwähnt, dass für diese Grafik der Detektionsgrundimpuls

$g_{\hspace{0.05cm}\rm Nyq} ( t )= g_0 \cdot {\rm si} \left ( \frac{\pi \cdot t}{T}\right)\cdot {\rm si} \left ( \frac{\pi \cdot t}{2 \cdot T}\right)$

mit trapezförmigem Spektrum und dem Rolloff–Faktor $r = 0.5$ zugrunde liegt, der schon auf der Seite Trapeztiefpass des Buches „Lineare zeitinvariante Systeme” behandelt wurde.

Erstes Nyquistkriterium im Frequenzbereich

Harry Nyquist hat die Bedingung für eine impulsinterferenzfreie Detektion nicht nur für den Zeitbereich formuliert, sondern 1928 auch das entsprechende Kriterium im Frequenzbereich angegeben.

$\text{Erstes Nyquistkriterium:}$ Erfüllt das Spektrum $G_d(f)$ des Detektionsgrundimpulses $g_d(t)$ die Bedingung

$\sum \limits_{\it k = -\infty}^{+\infty} G_d \left ( f - \frac{k}{T} \right)= g_0 \cdot T = {\rm const.} \hspace{0.05cm},$

so ist $g_d(t)$ ein Nyquistimpuls

mit äquidistanten Nulldurchgängen zu den Zeitpunkten $\nu \cdot T$ für $\nu \ne 0$ und
der Amplitude $g_d(t = 0) = g_0$ .

Hinweis: Der Beweis folgt auf der nächsten Seite.

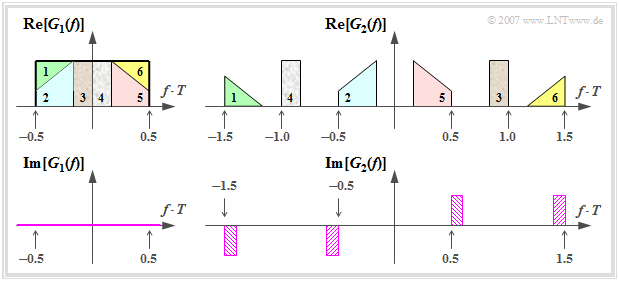
Zur Verdeutlichung des ersten Nyquistkriteriums

$\text{Beispiel 2:}$ Skizziert sind zwei Nyquistspektren $G_1(f)$ und $G_2(f)$ , die sich aus rechteckförmigen und dreieckförmigen Teilstücken zusammensetzen:

Das links skizzierte rein reelle Spektrum

$G_1(f) \hspace{-0.05cm}=\hspace{-0.05cm} \left\{ \begin{array}{c} g_0 \cdot T \\ 0 \\ \end{array} \right. \begin{array}{*{1}c} \text{für} \\ \text{für} \\ \end{array}\begin{array}{*{20}c} \vert f \vert \hspace{-0.08cm}<\hspace{-0.08cm} {1}/(2T), \\ \vert f \vert \hspace{-0.08cm}>\hspace{-0.08cm} {1}/(2T) \\ \end{array}$

erfüllt die oben formulierte Bedingung und zwar mit der kleinstmöglichen Bandbreite. Allerdings klingt der dazugehörige Nyquistimpuls

$g_1(t) = g_0 \cdot {\rm si}(\pi \cdot t/T)$ sehr langsam ab, nämlich asymptotisch mit

$1/t$ .

Der rechts oben dargestellte Realteil des Spektrums $G_2(f)$ wurde aus dem Rechteckspektrum $G_1(f)$ durch Verschiebung von Teilstücken um $1/T$ nach rechts oder links konstruiert.

$G_2(f)$ ist ebenfalls ein Nyquistspektrum wegen

$\sum \limits_{\it k = -\infty}^{+\infty} {\rm Re}\big[G_2 \left ( f - {k}/{T} \right)\big]= g_0 \cdot T \hspace{0.05cm}, \hspace{0.5cm}\sum \limits_{\it k = -\infty}^{+\infty} {\rm Im}\left[G_2 \big ( f - {k}/{T} \right)\big]= 0.$

Beim Imaginärteil heben sich die jeweils gleich schraffierten Anteile, die jeweils um $2/T$ auseinander liegen, auf.
Die Angabe des dazugehörigen Nyquistimpulses $g_2(t)$ ist allerdings sehr kompliziert.

Beweis des ersten Nyquistkriteriums

(1) Wir gehen von der ersten Nyquistbedingung im Zeitbereich aus:

$g_{\hspace{0.05cm}\rm Nyq}(\nu T) = \left\{ \begin{array}{c} g_0 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r} } \\ {\rm{f\ddot{u}r} } \\ \end{array}\begin{array}{*{20}c} \nu = 0 \hspace{0.05cm}, \\ \nu \ne 0 \hspace{0.1cm}. \\ \end{array}$

(2) Aus dem zweiten Fourierintegral erhält man somit für $\nu \ne 0$ :

$g_{\hspace{0.05cm}\rm Nyq}(\nu T) = \int_{-\infty}^{+\infty}G_{\rm Nyq}(f) \cdot {\rm e}^{ \hspace{0.05cm}{\rm j} \hspace{0.05cm}2 \pi f \hspace{0.05cm}\nu \hspace{0.05cm}T}\,{\rm d} f = 0 \hspace{0.05cm}.$

(3) Zerlegt man das Fourierintegral in Teilintegrale der Breite $1/T$ , so lauten die Bedingungsgleichungen:

$\sum_{k = -\infty}^{+\infty} \hspace{0.2cm} \int_{(k-1/2)/T}^{(k+1/2)/T}G_{\rm Nyq}(f) \cdot {\rm e}^{ \hspace{0.05cm}{\rm j} \hspace{0.05cm}2 \pi f \hspace{0.05cm}\nu \hspace{0.05cm}T}\,{\rm d} f = 0 \hspace{0.05cm}.$

(4) Mit der Substitution $f\hspace{0.08cm}' = f + k/T$ folgt daraus:

$\sum_{k = -\infty}^{+\infty} \hspace{0.2cm} \int_{-1/(2T)}^{1/(2T)}G_{\rm Nyq}(f\hspace{0.08cm}' - \frac{k}{T} ) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}2 \pi \hspace{0.05cm} \cdot \hspace{0.05cm} (f\hspace{0.08cm}'- k/T) \hspace{0.05cm} \cdot \hspace{0.05cm}\nu \hspace{0.05cm}T}\,{\rm d} f \hspace{0.08cm}' = 0 \hspace{0.05cm}.$

(5) Für alle ganzzahligen Werte von $k$ und $\nu$ gilt:

${\rm e}^{ - {\rm j} \hspace{0.05cm}2 \pi \hspace{0.05cm} k \hspace{0.05cm} \nu } = 1 \hspace{0.4cm} \Rightarrow \hspace{0.4cm}\sum_{k = - \infty}^{+\infty} \hspace{0.2cm} \int_{- 1/(2T)}^{1/(2T)}G_{\rm Nyq}(f\hspace{0.08cm}' - \frac{k}{T} ) \cdot {\rm e}^{ {\rm j} \hspace{0.05cm}2 \pi \hspace{0.02cm}f\hspace{0.08cm}' \hspace{0.02cm} \nu \hspace{0.05cm}T}\,{\rm d} f \hspace{0.08cm}' = 0 \hspace{0.05cm}.$

(6) Durch Vertauschen von Summation und Integration sowie Umbenennen von $f\hspace{0.08cm}'$ in $f$ folgt weiter:

$\int_{-1/(2T)}^{1/(2T)}\hspace{0.2cm} \sum_{k = - \infty}^{+\infty} G_{\rm Nyq}(f - \frac{k}{T} ) \cdot {\rm e}^{ {\rm j} \hspace{0.05cm}2 \pi \hspace{0.02cm}f \hspace{0.02cm} \nu \hspace{0.05cm}T}\,{\rm d} f = 0 \hspace{0.05cm}.$

(7) Diese Forderung ist für alle $\nu \ne 0$ nur dann zu erfüllen, wenn die unendliche Summe unabhängig von $f$ ist, also einen konstanten Wert besitzt:

$\sum_{k = -\infty}^{+\infty} G_{\rm Nyq}(f - \frac{k}{T} ) = K_{\rm Nyq} \hspace{0.05cm}.$

(8) Aus der vorletzten Gleichung erhält man gleichzeitig für $\nu = 0$ :

$\int_{-1/(2T)}^{1/(2T)}\hspace{0.2cm} \sum_{k = -\infty}^{+\infty} G_{\rm Nyq}(f - \frac{k}{T} ) \,{\rm d} f = K_{\rm Nyq} \cdot \frac{1}{T} = g_0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}K_{\rm Nyq} = g_0 \cdot T \hspace{0.05cm}.$

1/T–Nyquistspektren

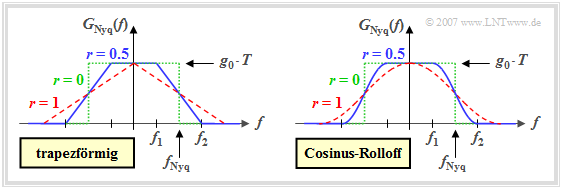
Besondere Bedeutung für die Digitalsignalübertragung haben solche Nyquistspektren, die auf den Frequenzbereich $-1/T \le f \le +1/T$ beschränkt und zusammenhängend sind. Die Grafik zeigt mit der Trapez–Charakteristik und der Cosinus–Rolloff–Charakteristik zwei diesbezügliche Varianten.

$1/T$ -Nyquistspektren

Für beide Nyquistspektren gilt in gleicher Weise:

Der Flankenabfall erfolgt zwischen den zwei Eckfrequenzen $f_1$ und $f_2$ punktsymmetrisch um die Nyquistfrequenz $f_{\rm Nyq} = (f_1+f_2)/2$ . Das heißt, dass für $0 \le f \le f_{\rm Nyq}$ gilt:

$G_{\rm Nyq}(f_{\rm Nyq}+f) + G_{\rm Nyq}(f_{\rm Nyq}-f) = g_0 \cdot T \hspace{0.05cm}.$

$G_{\rm Nyq}(f)$ ist für alle Frequenzen $|f| \le f_1$ konstant gleich $g_0 \cdot T$ und für $|f| \ge f_2$ identisch Null. Im Bereich zwischen $f_1$ und $f_2$ gilt:

$\frac{G_{\rm Nyq}(f)}{g_0 \cdot T } = \left\{ \begin{array}{c} \frac{f_2 - |f|}{f_2 -f_1 } \\ \\ \cos^2( \frac{\pi}{2}\cdot \frac{f_2 - |f|}{f_2 -f_1 }) \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{beim \hspace{0.15cm}Trapez}\hspace{0.05cm},} \\ \\ {\rm{\rm{beim \hspace{0.15cm}Cosinus-Rolloff}}\hspace{0.05cm}.} \\ \end{array}$

Zur Parametrisierung der Flankensteilheit verwenden wir den Rolloff–Faktor $r$ , der Werte zwischen $0$ und $1$ (einschließlich dieser Grenzen) annehmen kann:

$r = \frac{f_2 -f_1 } {f_2 +f_1 } \hspace{0.05cm}.$

Für $r = 0$ ⇒ $f_1 = f_2 = f_{\rm Nyq}$ ergibt sich das (grün–gepunktete) Rechteck-Nyquistspektrum.
Der Rolloff-Faktor $r = 1$ ⇒ $f_1 = 0, \ f_2 = 2 f_{\rm Nyq}$ steht für ein dreieckförmiges bzw. ein $\cos^2$ –Spektrum – je nachdem, von welcher der beiden oben abgebildeten Grundstrukturen man ausgeht. Diese Frequenzverläufe sind jeweils rot–gestrichelt eingezeichnet.

Hinweis: In der Literatur wird der Rolloff–Faktor teilweise auch mit $\alpha$ („alpha”) bezeichnet.

Zeitbereichsbeschreibung der 1/T–Nyquistspektren

Betrachten wir nun die Nyquistimpulse. Beim trapezförmigem Spektrum mit Rolloff–Faktor $r$ erhält man:

$g_{_{\rm Trapez}} ( t )= g_0 \cdot {\rm si} \left ( \frac{\pi \cdot t}{T}\right)\cdot {\rm si} \left ( \frac{\pi \cdot r \cdot t}{T}\right) \hspace{0.5cm}{\rm mit }\hspace{0.5cm}{\rm si}(x) = {\rm sin}(x)/x .$

Dagegen liefert die Fourierrücktransformation des Cosinus–Rolloff–Spektrums (kurz: CRO–Spektrum):

$g_{_{\rm CRO}} ( t )= g_0 \cdot {\rm si} \left ( \frac{\pi \cdot t}{T}\right)\cdot \frac{\cos(\pi \cdot r \cdot t/T)}{1 - (2 \cdot r \cdot t/T)^2 } \hspace{0.3cm}{\rm mit }\hspace{0.3cm}{\rm si}(x) = {\rm sin}(x)/x.$

Diese beiden Nyquistimpulse kann man mit dem interaktiven Applet Frequenzgang und Impulsantwort $($ mit der Einstellung $\Delta \cdot f = 1)$ betrachten und sich dabei den Einfluss des Rolloff–Faktors $r$ verdeutlichen.

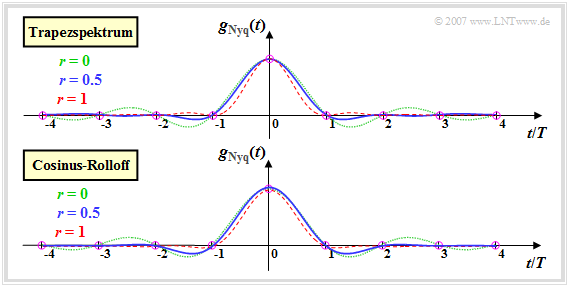
Die folgende obere Grafik zeigt den Nyquistimpuls mit Trapezspektrum für verschiedene Rolloff–Faktoren. Unten ist der entsprechende Zeitverlauf für das Cosinus–Rolloff–Spektrum dargestellt. Man erkennt:

Nyquistimpulse mit Trapez- und Cosinus-Rolloff-Spektrum

Je kleiner der Rolloff–Faktor $r$ ist, desto langsamer erfolgt der Abfall des Nyquistimpulses. Diese Aussage trifft sowohl für das Trapez– als auch für das Cosinus–Rolloff–Spektrum zu.
Im Grenzfall $r \to 0$ ergibt sich in beiden Fällen das rechteckförmige Nyquistspektrum und der $\rm si$ –förmige Nyquistimpuls, der asymptotisch mit $1/t$ abklingt (dünne grüne Kurven).
Bei einem mittleren Rolloff $(r \approx 0.5)$ sind die ersten Überschwinger beim Trapezspektrum geringer als beim CRO–Spektrum, da hier bei gegebenem $r$ die Nyquistflanke flacher verläuft (blaue Kurven).
Mit dem Rolloff–Faktor $r = 1$ wird im Frequenzbereich aus dem Trapez ein Dreieck und aus dem CRO–Spektrum das Cosinus–Quadrat–Spektrum. In den Grafiken auf der letzten Seite sind diese Spektralfunktionen rot gezeichnet.
Mit $r = 1$ erfolgt der asymptotische Abfall der oberen Zeitfunktion (gemäß dem Trapezspektrum) mit $1/t^2$ und der Abfall der unteren Zeitfunktion (gemäß dem CRO–Spektrum) mit $1/t^3$ .
Das bedeutet: Nach längerer Zeit ist der CRO–Nyquistimpuls besser eingeschwungen als der Trapez–Nyquistimpuls.

Zweites Nyquistkriterium

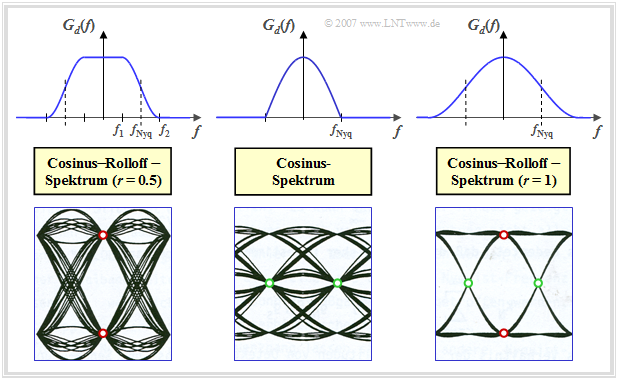
Vor der exakten mathematischen Definition soll anhand von Grafiken veranschaulicht werden, welche Bedeutung das zweite Nyquistkriterium zur Bewertung eines Digitalsystems besitzt. In der Grafik sind für drei Beispiele von Nyquistsystemen jeweils dargestellt:

oben das Nyquistspektrum $G_d(f)$ ,
unten das dazugehörige Augendiagramm im Vorgriff auf das dritte Hauptkapitel.

Zur Verdeutlichung von erstem und zweitem Nyquistkriterium

Interpretation:

Die linke Grafik zeigt das Augendiagramm eines Nyquistsystems mit Cosinus–Rolloff–Charakteristik, wobei der Rolloff–Faktor $r= 0.5$ gewählt wurde. Da hier das erste Nyquistkriterium erfüllt ist (es besteht eine Punktsymmetrie um die Nyquistfrequenz $f_{\rm Nyq}$ , ergibt sich für die vertikale Augenöffnung zum Zeitpunkt $t = 0$ der größtmögliche Wert $2 \cdot g_d(0)$ . Alle Augenlinien gehen zum Zeitpunkt $t = 0$ durch einen der beiden rot markierten Punkte ⇒ das Auge ist vertikal maximal geöffnet.

Das mittlere Spektrum weist keine Symmetrie bezüglich des Flankenabfalls auf, so dass hier das erste Nyquistkriterium nicht erfüllt ist – im Gegensatz zum zweiten. Alle Augenlinien schneiden hier die Zeitachse zu den selben Zeiten (markiert durch die grünen Punkte), was beispielsweise die Taktwiedergewinnung mittels einer PLL (Phase-Locked Loop ) erleichtert. Bei Erfüllung des zweiten Nyquistkriteriums ist die horizontale Augenöffnung maximal gleich der Symboldauer $T$ ⇒ das Auge ist horizontal maximal geöffnet.

Das rechte Augendiagrammm verdeutlicht, dass beim CRO–Spektrum mit $r = 1$ sowohl das erste als auch das zweite Nyquistkriterium erfüllt werden. Der Nyquistimpuls

$g_d ( t )= g_0 \cdot \frac{\pi }{4}\cdot {\rm si} \left ( \frac{\pi \cdot t}{T}\right)\cdot \left [ {\rm si}(\pi \cdot (\frac{t}{T} + \frac{1}{2}) + {\rm si}(\pi \cdot (\frac{t}{T} - \frac{1}{2})\right]$

weist hier die erforderlichen Nulldurchgänge bei

$t = \pm T$ ,

$t = \pm 1.5T$ ,

$t = \pm 2T$ ,

$t = \pm 2.5T$ , ... auf, nicht jedoch bei

$t = \pm 0.5T$ . Die Impulsamplitude ist

$g_d(t = 0) = g_0$ . Hinweis: Kein anderer Impuls erfüllt gleichzeitig das erste und das zweite Nyquistkriterium.

$\text{Zusammenfassung der Nyquistkriterien:}$

(1) In Erinnerung an den Physiker Harry Nyquist bezeichnen wir einen Detektionsgrundimpuls $g_d( t)$ mit den Eigenschaften

$g_d ( t= 0) \ne 0, \hspace{1cm} g_d ( t)= 0 \hspace{0.3cm}{\rm{f\ddot{u}r} }\hspace{0.3cm} t = \pm T, \pm 2T,\pm 3T,\hspace{0.05cm}\text{...}$

als Nyquist–1–Impuls

$g_{\hspace{0.05cm}\rm Nyq-1}(t)$ . Dieser erfüllt das erste Nyquistkriterium und führt zur maximalen vertikalen Augenöffnung.

(2) Ein Impuls $g_{\hspace{0.05cm}\rm Nyq-2}(t)$ , der das zweite Nyquistkriterium erfüllt, muss Nulldurchgänge bei $t = \pm 1.5T$ , $t = \pm 2.5T$ , ... besitzen:

$g_d ( t= 0.5) \ne 0, \hspace{0.8cm} g_d ( t)= 0 \hspace{0.3cm}{\rm{f\ddot{u}r} }\hspace{0.3cm} t = \pm 1.5T, \ \pm 2.5T,\ \pm 3.5T,\hspace{0.05cm}\text{...}$

Ein solcher Nyquist–2–Impuls führt zur maximalen horizontalen Augenöffnung.

(3) Ein Nyquist–2–Impuls kann immer als Summe zweier um $t = \pm T/2$ verschobener Nyquist–1–Impulse dargestellt werden:

$g_{\rm Nyq-2} ( t )= g_{\rm Nyq-1} ( t +T/2)+g_{\rm Nyq-1} ( t -T/2)\hspace{0.05cm}.$

(4) Im Frequenzbereich lautet das zweite Nyquistkriterium (siehe [ST85] ^[1]):

$\sum_{k = -\infty}^{+\infty} \frac {G_d \left ( f -k/T \right)}{\cos(\pi \cdot f \cdot T - k \cdot \pi)}= {\rm const.}$

$\text{Beispiel 3:}$ Ausgehend vom Nyquist–1–Impuls $g_{\rm Nyq-1}( t )= g_0 \cdot {\rm si}(\pi \cdot t/T)$ lautet der dazugehörige Nyquist–2–Impuls:

$g_{\rm Nyq-2}( t ) = g_0 \cdot \left [ {\rm si}(\pi \cdot \frac{t + T/2}{T}) + {\rm si}(\pi \cdot \frac{t- T/2}{T}) \right] =\frac{2 \cdot g_0}{\pi} \cdot \frac{\cos(\pi \cdot t/T)}{1 - (2 \cdot t/T)^2}\hspace{0.05cm}.$

Aufgrund der Begrenzung des Spektrums $G_{\rm Nyq-1}( f)$ auf den Bereich $\vert f \vert \le f_{\rm Nyq} = 1/(2T)$ beschränkt sich in obiger Gleichung (4) die Summe auf den Term mit $k = 0$ und man erhält:

$G_{\rm Nyq-2}(f) = \left\{ \begin{array}{c} g_0 \cdot T \cdot \cos(\pi/2 \cdot f/f_{\rm Nyq}) \\ \\ 0 \\\end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r} }\hspace{0.15cm} \vert f \vert < f_{\rm Nyq}\hspace{0.05cm}, \\ \\ {\rm{sonst} }\hspace{0.05cm}. \\ \end{array}$

Dieser Frequenzverlauf und das dazugehörige Augendiagramm ist in in der mittleren Spalte der obigen Grafik skizziert.
Aus der unteren Grafik erkennt man deutlich die Erfüllung des zweiten Nyquistkriteriums.

Aufgaben zum Kapitel

Aufgabe 1.4: Nyquistkriterien

Aufgabe 1.4Z: Komplexes Nyquistspektrum

Aufgabe 1.5: Cosinus-Quadrat-Spektrum

Quellenverzeichnis

↑ Söder, G.; Tröndle, K.: Digitale Übertragungssysteme - Theorie, Optimierung & Dimensionierung der Basisbandsysteme. Berlin – Heidelberg: Springer, 1985.

[1] Söder, G.; Tröndle, K.: Digitale Übertragungssysteme - Theorie, Optimierung & Dimensionierung der Basisbandsysteme. Berlin – Heidelberg: Springer, 1985.

[1]