Contents
- 1 # ÜBERBLICK ZUM VIERTEN HAUPTKAPITEL #
- 2 Hard Decision vs. Soft Decision
- 3 Zuverlässigkeitsinformation – Log Likelihood Ratio
- 4 Symbolweise Soft–in Soft–out Decodierung
- 5 Zur Berechnung der extrinsischen L–Werte
- 6 BCJR–Decodierung: Vorwärts–Rückwärts–Algorithmus
- 7 Grundstruktur von verketteten Codiersystemen
- 8 Aufgaben zum Kapitel
- 9 Quellenverzeichnis
# ÜBERBLICK ZUM VIERTEN HAUPTKAPITEL #
Das letzte Hauptkapitel des Kanalcodierungsbuches beschreibt iterative Decodierverfahren, wie sie in den meisten heutigen (2017) Kommunikationssystemen eingesetzt werden. Dies hat folgende Gründe:
- Um sich der Kanalkapazität anzunähern, benötigt man sehr lange Codes.
- Für lange Codes ist aber eine blockweise Maximum–Likelihood–Decodierung nahezu unmöglich.
Die Decoder–Komplexität lässt sich bei nahezu gleicher Qualität deutlich herabsetzen, wenn man zwei (oder mehrere) kurze Kanalcodes miteinander verknüpft und beim Empfänger die jeweils neu gewonnene (Soft–)Information in mehreren Schritten – also iterativ – zwischen den Decodern austauscht.
Der Durchbruch auf dem Gebiet gelang Anfang der 1990er Jahre mit der Erfindung der Turbo–Codes durch Claude Berrou und kurz darauf mit der Wiederentdeckung der Low–density Parity–check Codes durch David J. C. MacKay und Radford M. Neal, nachdem die schon 1961 von Robert G. Gallager entwickelten LDPC–Codes zwischenzeitlich in Vergessenheit geraten waren.
Im Einzelnen werden im vierten Hauptkapitel behandelt:
- Eine Gegenüberstellung von Hard Decision und Soft Decision,
- die Quantifizierung von Zuverlässigkeitsinformation durch Log Likelihood Ratios (LLR),
- das Prinzip der symbolweisen Soft–in Soft–out (SISO) Decodierung,
- die Definition von Apriori–L–Wert, Aposteriori–L–Wert und extrinsischem L–Wert,
- die Grundstruktur von seriell verketteten bzw. parallel verketteten Codiersystemen,
- die Eigenschaften von Produkt–Codes und deren Hard Decision Decodierung,
- die Grundstruktur, der Decodieralgorithmus und die Leistungsfähigkeit der Turbo–Codes,
- Grundlegendes zu den Low–density Parity–check Codes und deren Anwendungen.
Hard Decision vs. Soft Decision
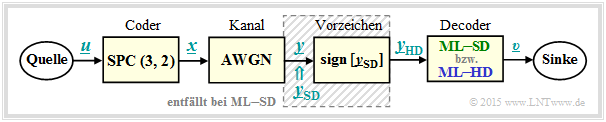
Zur Hinleitung auf die hier behandelte Thematik betrachten wir das folgende Nachrichtenübertragungssystem mit Codierung.
Im Weiteren werden alle Symbole in bipolarer Darstellung angegeben: „$0$” → „$+1$” und „$1$” → „$-1$”.
- Die Symbolfolge $\underline{u} = (u_1, \ u_2)$ wird der Coderfolge $\underline{x} = (x_1, \ x_2, \ x_3) = (u_1, \ u_2, \ p)$ zugeordnet, wobei für das Paritybit $p = u_1 ⊕ u_2$ gilt ⇒ Single Parity–check Code ⇒ ${\rm SPC} (3, 2, 2)$.
- Der AWGN–Kanal verändert die Binärsymbole $x_i ∈ \{+1, \ –1\}$ zu reellwertigen Ausgangswerten $y_i$, zum Beispiel gemäß $\text{Kanal 4}$ der unteren Tabelle: $x_1 = +1$ ⇒ $y_1 = +0.9$, $x_2 = \, -1$ ⇒ $y_2 = +0.1$ und $x_3 = \, -1$ ⇒ $y_3 = +0.1$.
- Die Decodierung geschieht gemäß dem Kriterium Maximum-Likelihood $\text{(blockwise ML)}$, wobei zwischen Hard Decision $\rm {(ML–HD)}$ und Soft Decision $\rm {(ML–SD)}$ zu unterscheiden ist.
- Das gesamte Blockschaltbild entspricht $\rm ML–HD$. Hier werden zur Decodierung nur die Vorzeichen der AWGN–Ausgangswerte ⇒ $y_{\rm HD, \ \it i} = {\rm sign}\big [y_{\rm SD, \ \it i}\big ]$ ausgewertet. Bei Soft Decision $\rm {(ML–SD)}$ verzichtet man auf den schraffierten Block und wertet direkt die wertkontinuierlichen Eingangsgrößen $y_{\rm SD, \ \it i}$ aus.
Für alle Spalten dieser Tabelle wird vorausgesetzt:
- der Nachrichtenblock $\underline{u} = (0, 1)$, bipolar darstellbar als $(+1, \, –1)$,
- der ${\rm SPC} \ (3, 2)$–codierte Block $\underline{x} = (0, 1, 1)$ bzw. in Bipolardarstellung $(+1, \, -1, \, -1)$.
Die vier Spalten unterscheiden sich also nur durch unterschiedliche AWGN–Realisierungen.
$\text{Definition:}$ Aus der Beispieltabelle erkennt man:
- $\text{Hard Decision:}$ Die Symbolfolge $\underline{v}_{\rm HD}$ ergibt sich aus den hart entschiedenen Kanalwerten $\underline{y}_{\rm HD}$ (blaue Hinterlegung).
Bei unserem Beispiel werden nur die Konstellationen gemäß $\text{Kanal 1}$ und $\text{Kanal 2}$ fehlerfrei decodiert.
- $\text{Soft Decision:}$ Die Symbolfolge $\underline{v}_{\rm SD}$ ergibt sich aus den „weichen” Kanalausgangswerten $\underline{y}_{\rm SD}$ (grüne Hinterlegung).
Nun wird in diesem Beispiel auch bei $\text{Kanal 3}$ richtig entschieden.
Die Einträge in der obigen Beispieltabelle sind wie folgt zu interpretieren:
- Bei idealem Kanal ⇒ $\text{Kanal 1}$ ⇒ $\underline{x} = \underline{y}_{\rm SD} = \underline{y}_{\rm HD}$ gibt es keinen Unterschied zwischen der (blauen) herkömmlichen Hard Decision–Variante $\rm {(ML–HD)}$ und der (grünen) Soft Decision–Variante $\rm {(ML–SD)}$.
- Die Einstellung entsprechend $\text{Kanal 2}$ demonstriert geringe Signalverfälschungen. Wegen $\underline{y}_{\rm HD} = \underline{x}$ (das heißt, dass der Kanal die Vorzeichen nicht verfälscht) liefert auch $\rm ML–HD$ das richtige Ergebnis $\underline{v}_{\rm HD} = \underline{u}$.
- Beim $\text{Kanal 3}$ gilt $\underline{y}_{\rm HD} ≠ \underline{x}$ und es gibt auch keine ${\rm SPC} \ (3, 2)$–Zuordnung $\underline{u}$ ⇒ $\underline{y}_{\rm HD}$. Der ML–Decoder vermeldet hier durch die Ausgabe $\underline{v}_{\rm HD} = \rm (E, \ E)$, dass er bei der Decodierung dieses Blocks gescheitert ist. „$\rm E$” steht für Erasure (deutsch: Auslöschung).
- Auch der Soft Decision Decoder erkennt, dass eine Decodierung anhand der Vorzeichen nicht funktioniert. Anhand der $\underline{y}_{\rm SD}$–Werte erkennt er aber, dass mit großer Wahrscheinlichkeit das zweite Bit verfälscht wurde und entscheidet sich für die richtige Symbolfolge $\underline{v}_{\rm SD} = (+1, \, -1) = \underline{u}$.
- Bei $\text{Kanal 4}$ werden durch den AWGN–Kanal sowohl die Vorzeichen von Bit 2 als auch von Bit 3 verändert, was zum Ergebnis $\underline{v}_{\rm HD} = (+1, +1) ≠ \underline{u}(+1, \, -1)$ führt ⇒ ein Blockfehler und gleichzeitig ein Bitfehler. Auch der Soft Decision Decoder liefert hier das gleiche falsche Ergebnis.
Die Decodiervariante „ML–SD” bietet gegenüber „ML–HD” zudem den Vorteil, dass man relativ einfach jedes Decodierergebnis mit einem Zuverlässigkeitswert versehen kann (in obiger Tabelle ist dieser allerdings nicht angegeben). Dieser Zuverlässigkeitswert
- hätte bei $\text{Kanal 1}$ seinen Maximalwert,
- wäre bei $\text{Kanal 2}$ deutlich kleiner,
- läge bei $\text{Kanal 3}$ und $\text{Kanal 4}$ nahe bei Null.
Zuverlässigkeitsinformation – Log Likelihood Ratio
Es sei $x ∈ \{+1, \, -1\}$ eine binäre Zufallsvariable mit den Wahrscheinlichkeiten ${\rm Pr}(x = +1)$ und ${\rm Pr}(x = \, -1)$. Für die Codierungstheorie erweist es sich als zweckmäßig hinsichtlich der Rechenzeiten, wenn man anstelle der Wahrscheinlichkeiten ${\rm Pr}(x = ±1)$ den natürlichen Logarithmus des Quotienten heranzieht.
$\text{Definition:}$ Das Log–Likelihood–Verhältnis (kurz: der $L$–Wert, englisch: Log–Likelihood Ratio, LLR) der Zufallsgröße $x ∈ \{+1, \, -1\}$ lautet:
- \[L(x)={\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(x = +1)}{ {\rm Pr}(x = -1)}\hspace{0.05cm}.\]
Bei unipolarer/symbolhafter Darstellung $(+1 → 0$ und $-1 → 1)$ gilt entsprechend mit $\xi ∈ \{0, \, 1\}$:
- \[L(\xi)={\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(\xi = 0)}{ {\rm Pr}(\xi = 1)}\hspace{0.05cm}.\]
Nachfolgend ist der nichtlineare Zusammenhang zwischen ${\rm Pr}(x = ±1)$ und $L(x)$ angegeben. Ersetzt man ${\rm Pr}(x = +1)$ durch ${\rm Pr}(\xi = 0)$, so gibt die mittlere Zeile den $L$–Wert der unipolaren Zufallsgröße $\xi$ an.
Man erkennt:
- Der wahrscheinlichere Zufallswert von $x ∈ \{+1, \, -1\}$ ist durch das Vorzeichen ⇒ ${\rm sign} \ L(x)$ gegeben.
- Dagegen gibt der Betrag ⇒ $|L(x)|$ die Zuverlässigkeit für das Ergebnis ${\rm sign}(L(x))$ an.
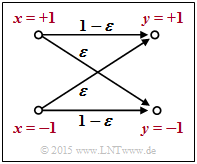
$\text{Beispiel 1:}$ Wir betrachten das skizzierte BSC–Modell mit bipolarer Darstellung. Hier gilt mit der Verfälschungswahrscheinlichkeit $\varepsilon = 0.1$ sowie den beiden Zufallsgrößen $x ∈ \{+1, \, -1\}$ und $y ∈ \{+1, \, -1\}$ am Eingang und Ausgang des Kanals:
- \[L(y\hspace{0.05cm}\vert\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{ {\rm Pr}(y\hspace{0.05cm}\vert\hspace{0.05cm}x = +1) }{ {\rm Pr}(y\hspace{0.05cm}\vert\hspace{0.05cm}x = -1)} = \left\{ \begin{array}{c} {\rm ln} \hspace{0.15cm} \big[(1 - \varepsilon)/\varepsilon \big]\\ {\rm ln} \hspace{0.15cm}\big [\varepsilon/(1 - \varepsilon)\big] \end{array} \right.\quad \begin{array}{*{1}c} {\rm f\ddot{u}r} \hspace{0.15cm} y = +1, \\ {\rm f\ddot{u}r} \hspace{0.15cm} y = -1. \\ \end{array}\]
Beispielsweise ergeben sich für $\varepsilon = 0.1$ folgende Zahlenwerte (vergleiche obere Tabelle):
- \[L(y = +1\hspace{0.05cm}\vert\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \frac{0.9}{0.1} = +2.197\hspace{0.05cm}, \hspace{0.8cm} L(y = -1\hspace{0.05cm}\vert\hspace{0.05cm}x) = -2.197\hspace{0.05cm}.\]
Dieses Beispiel zeigt, dass man die so genannte $L$–Wert–Algebra auch auf bedingte Wahrscheinlichkeiten anwenden kann.
In der Aufgabe 4.1Z wird das BEC–Modell in ähnlicher Weise beschrieben.
$\text{Beispiel 2:}$ In einem weiteren Beispiel betrachten nun den AWGN–Kanal mit den bedingten Wahrscheinlichkeitsdichtefunktionen
- \[f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=+1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert\hspace{0.05cm}x=+1 )\hspace{-0.1cm} = \hspace{-0.1cm} \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y-1)^2}/(2\sigma^2) } \hspace{0.05cm},\]
- \[f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=-1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert\hspace{0.05cm}x=-1 )\hspace{-0.1cm} = \hspace{-0.1cm} \frac {1}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y+1)^2}/(2\sigma^2) } \hspace{0.05cm}.\]
In der Grafik sind zwei beispielhafte Gaußfunktionen als blaue bzw. rote Kurve dargestellt.
Die gesamte WDF des Ausgangssignals $y$ ergibt sich aus der (gleich) gewichteten Summe:
- \[f_{y } \hspace{0.05cm} (y ) = 1/2 \cdot \big [ f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=+1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert\hspace{0.05cm}x=+1 ) \hspace{0.1cm} + \hspace{0.1cm} f_{y \hspace{0.03cm}\vert \hspace{0.03cm}x=-1 } \hspace{0.05cm} (y \hspace{0.05cm}\vert \hspace{0.05cm}x=-1 ) \big ] \hspace{0.05cm}.\]
Wir berechnen nun die Wahrscheinlichkeit, dass der Empfangswert $y$ in einem (sehr) schmalen Intervall der Breite $\Delta$ um $y_0 = 0.25$ liegt. Man erhält näherungsweise
- \[{\rm Pr} (\vert y - y_0\vert \le{\it \Delta}/2 \hspace{0.05cm} \Big \vert \hspace{0.05cm}x=+1 )\hspace{-0.1cm} \approx \hspace{-0.1cm} \frac {\it \Delta}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y_0-1)^2}/(2\sigma^2) } \hspace{0.05cm},\]
- \[{\rm Pr} (\vert y - y_0\vert \le {\it \Delta}/2 \hspace{0.05cm} \Big \vert \hspace{0.05cm}x=-1 )\hspace{-0.1cm} \approx \hspace{-0.1cm} \frac {\it \Delta}{\sqrt{2\pi} \cdot \sigma } \cdot {\rm e} ^{ - {(y_0+1)^2}/(2\sigma^2) } \hspace{0.05cm}.\]
Die etwas größeren senkrechten Striche bezeichnen die Bedingungen, die kleineren die Betragsbildung.
Der $L$–Wert der bedingten Wahrscheinlichkeit in Vorwärtsrichtung $($das bedeutet: Ausgang $y$ für einen gegebenen Eingang $x)$ ergibt sich somit als der Logarithmus des Quotienten beider Ausdrücke:
- \[L(y = y_0\hspace{0.05cm}\vert\hspace{0.05cm}x) = {\rm ln} \hspace{0.15cm} \left [ \frac{{\rm e} ^{ - {(y_0-1)^2}/(2\sigma^2)}}{{\rm e} ^{ - {(y_0+1)^2}/(2\sigma^2)}} \right ] = {\rm ln} \left [ {\rm e} ^{ - [ {(y_0-1)^2}+{(y_0+1)^2}]/(2\sigma^2)} \right ] = \frac{(y_0+1)^2-(y_0-1)^2}{2\cdot \sigma^2} = \frac{2 \cdot y_0}{\sigma^2}\hspace{0.05cm}. \]
Ersetzen wir nun die Hilfsgröße $y_0$ durch die (allgemeine) Zufallsgröße $y$ am AWGN–Ausgang, so lautet das Endergebnis:
- \[L(y \hspace{0.05cm}\vert\hspace{0.05cm}x) = {2 \cdot y}/{\sigma^2} =K_{\rm L} \cdot y\hspace{0.05cm}. \]
Hierbei ist $K_{\rm L} = 2/\sigma^2$ eine Konstante, die allein von der Streuung der Gaußschen Störung abhängt.
Symbolweise Soft–in Soft–out Decodierung
Wir gehen nun von einem $(n, \ k)$–Blockcode aus, wobei das Codewort $\underline{x} = (x_1, \ \text{...} \ , \ x_n)$ durch den Kanal in das Empfangswort $\underline{y} = (y_1, \ \text{...} \ , \ y_n)$ verfälscht wird.
- Bei langen Codes ist eine Maximum–a–posteriori–Entscheidung auf Blockebene – kurz: $\text{ block–wise MAP}$ – sehr aufwändig.
- Man müsste unter den $2^k $ zulässigen Codeworten $\underline{x}_j ∈ \mathcal{C}$ dasjenige mit der größten Rückschlusswahrscheinlichkeit (englisch: A Posteriori Probability, APP) finden.
- Das auszugebende Codewort $\underline{z}$ wäre in diesem Fall $\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}j} \hspace{0.03cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}j} |\hspace{0.05cm} \underline{y} ) \hspace{0.05cm}.$
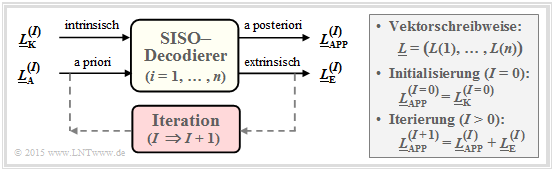
Eine zweite Möglichkeit ist die Decodierung auf Bitebene. Der dargestellte symbolweise (oder bitweise) $\text{Soft–in Soft–out Decoder}$ hat die Aufgabe, alle Codewortbits $x_i ∈ \{0, \, 1\}$ entsprechend maximaler Rückschlusswahrscheinlichkeit ${\rm Pr}(x_i | \underline{y})$ zu decodieren. Mit der Laufvariablen $i = 1, \text{...} , \ n$ gilt dabei:
- Der entsprechende $L$–Wert (englisch: Log Likelihood Ratio, LLR) für das $i$–te Codebit lautet:
- \[L_{\rm APP} (i) = L(x_i\hspace{0.05cm}|\hspace{0.05cm}\underline{y}) = {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}(x_i = 0\hspace{0.05cm}|\hspace{0.05cm}\underline{y})}{{\rm Pr}(x_i = 1\hspace{0.05cm}|\hspace{0.05cm}\underline{y})}\hspace{0.05cm} . \]
- Der Decoder arbeitet iterativ. Bei der Initialisierung $($in der Grafik gekennzeichnet durch den Parameter $I = 0)$ ist $L_{\rm APP}(i) = L_{\rm K}(i)$, wobei das Kanal–LLR $L_{\rm K}(i)$ durch den Empfangswert $y_i$ gegeben ist.
- Berechnet wird zudem der extrinsische $L$–Wert $L_{\rm E}(i)$, der die gesamte Information quantifiziert, die alle anderen Bits $(j ≠ i)$ aufgrund der Code–Eigenschaften über das betrachtete $i$–te Bit liefern.
- Bei der nächsten Iteration $($ab $I = 1)$ wird $L_{\rm E}(i)$ bei der Berechnung von $L_{\rm APP}(i)$ als Apriori–Information $L_{\rm A}(i)$ berücksichtigt. Für das neue Aposteriori–LLR in der Iteration $I + 1$ gilt somit:
- \[L_{\hspace{0.1cm}\rm APP}^{(I+1)} (i) = L_{\hspace{0.1cm}\rm APP}^{(I)} (i) + L_{\hspace{0.1cm}\rm A}^{(I+1)} (i) = L_{\hspace{0.1cm}\rm APP}^{(I)} (i) + L_{\hspace{0.1cm}\rm E}^{(I)} (i)\hspace{0.05cm} . \]
- Die Iterationen werden fortgesetzt, bis alle Beträge $|L_{\rm APP}(i)|$ größer sind als ein vorzugebender Wert. Das wahrscheinlichste Codewort $\underline{z}$ ergibt sich dann aus den Vorzeichen aller $L_{\rm APP}(i)$, mit $i = 1, \ \text{...} , \ n$.
- Bei einem systematischen Code geben die ersten $k$ Bit von $\underline{z}$ das gesuchte Informationswort an, das mit großer Wahrscheinlichkeit mit der gesendeten Nachricht $\underline{u}$ übereinstimmen wird.
Diese Beschreibung des SISO–Decodierers nach [Bos98][1] soll an dieser Stelle in erster Linie die unterschiedlichen $L$–Werte verdeutlichen. Das große Potential der symbolweisen Decodierung erkennt man erst im Zusammenhang mit verketteten Codiersystemen.
Zur Berechnung der extrinsischen L–Werte
Die Schwierigkeit bei der symbolweisen iterativen Decodierung ist im allgemeinen die Bereitstellung der extrinsischen $L$–Werte $L_{\rm E}(i)$. Bei einem Code der Länge $n$ gilt hierbei für die Laufvariable: $i = 1, \ \text{...} , \ n$.
$\text{Definition:}$ Der extrinsische $L$–Wert (englisch: extrinsic LLR ) ist ein Maß für die Informationen, den die anderen Symbole $(j ≠ i)$ des Codewortes über das $i$–te Codesymbol liefern, ausgedrückt als Log–Likelihood–Verhältnis. Wir benennen diesen Kennwert mit $L_{\rm E}(i)$.
Wir berechnen nun die extrinsischen $L$–Werte $L_{\rm E}(i)$ für zwei beispielhafte Codes.
$\text{Repetition Code}$ ⇒ ${\rm RC} \ (n, 1, n)$
Ein Wiederholungscode zeichnet sich dadurch aus, dass alle $n$ Codesymbole $x_i ∈ \{0, \, 1\}$ identisch sind. Der extrinsische $L$–Wert für das $i$–ten Symbol ist hier sehr einfach anzugeben und lautet:
- \[L_{\rm E}(i) = \hspace{0.05cm}\sum_{j \ne i} \hspace{0.1cm} L_j \hspace{0.3cm}{\rm mit}\hspace{0.3cm}L_j = L_{\rm APP}(j) \hspace{0.05cm}.\]
- Ist die Summe über alle $L_{j ≠ i}$ positiv, so bedeutet dies aus Sicht der anderen $L$–Werte eine Präferenz für die Entscheidung $x_i = 0$.
- Bei negativer Summe ist dagegen $x_i = 1$ wahrscheinlicher.
- $L_{\rm E}(i) = 0$ erlaubt keine Vorhersage.
$\text{Beispiel 5:}$ Wir betrachten die Decodierung des Wiederholungscodes $\text{RC (4, 1,4)}$. Wir gehen dabei von drei verschiedene Annnahmen für das Log Likelihood Ratio $\underline{L}_{\rm A}^{(I=0)} = \underline{L}_{\rm APP}$ aus.
$\text{Decodierbeispiel (A):}$
- $$\underline{L}_{\rm APP} = (+1, -1, +3, -1)\text{:}$$
- $$L_{\rm E}(1) = -1+3-1 = +1\hspace{0.05cm},$$
- $$L_{\rm E}(2) = +1+3-1 = +3\hspace{0.05cm},$$
- $$L_{\rm E}(3) = +1-1 -1= -1\hspace{0.05cm},$$
- $$L_{\rm E}(4) = +1-1 +3 = +3\hspace{0.05cm}$$
- $$\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{L}_{\rm E}^{(I=0)}= (+1, +3, -1, +3) \hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{L}_{\rm A}^{(I=1)}=\underline{L}_{\rm A}^{(I=0)}+ \underline{L}_{\rm E}^{(I=0)}= (+2, +2, +2, +2)$$
- Zu Beginn $(I=0)$ weisen die positiven $L_{\rm E}$–Werte auf $x_1 = 0$, $x_2 = 0$ und $x_4 = 0$ hin, während $x_3 =1$ wahrscheinlicher ist.
- Bereits nach einer Iteration $(I=1)$ sind alle $L_{\rm A}$–Werte positiv ⇒ Informationsbit wird als $u = 0$ decodiert.
- Weitere Iterationen bringen nichts.
$\text{Decodierbeispiel (B):}$ $$\underline{L}_{\rm APP} = (+1, +1, -4, +1)\text{:}$$ $$\underline{L}_{\rm E}^{(I=0)} = \ (-2, -2, +3, -2)$$
- Obwohl zu Beginn drei Vorzeichen falsch waren, sind nach zwei Iterationen alle $L_{\rm A}$–Werte negativ.
- Das Informationsbit wird als $u = 1$ decodiert.
$\text{Decodierbeispiel (C):}$ $$\underline{L}_{\rm APP} = (+1, +1, -3, +1)\text{:}$$ $$\underline{L}_{\rm E}^{(I=0)} = (-1, -1, +3, -1)$$
- Alle $L_{\rm A}$–Werte sind schon nach einer Iteration Null.
- Das Informationsbit kann nicht decodiert werden, obwohl die Ausgangslage nicht viel schlechter war als bei $\rm (B)$.
- Weitere Iterationen bringen auch hier nichts.
$\text{Single Parity–check Code}$ ⇒ ${\rm SPC} \ (n, \ n \, -1, \ 2)$
Bei jedem Single Parity–check Code ist die Anzahl der Einsen in jedem Codewort geradzahlig. Oder anders ausgedrückt: Für jedes Codewort $\underline{x}$ ist das Hamming–Gewicht $w_{\rm H}(\underline{x})$ geradzahlig.
$\text{Definition:}$ Das Codewort $\underline{x}^{(–i)}$ beinhalte alle Symbole mit Ausnahme von $x_i$ ⇒ Vektor der Länge $n -1$. Damit lautet der extrinsische $L$–Wert bezüglich dieses $i$–ten Symbols, wenn $\underline{x}$ empfangen wurde:
- \[L_{\rm E}(i) = {\rm ln} \hspace{0.15cm}\frac{ {\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} gerade} \hspace{0.05cm} \vert\hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]}{ {\rm Pr} \left [w_{\rm H}(\underline{x}^{(-i)})\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade} \hspace{0.05cm} \vert \hspace{0.05cm}\underline{y} \hspace{0.05cm}\right ]} \hspace{0.05cm}.\]
Wie in der Aufgabe 4.4 gezeigt werden soll, kann hierfür auch geschrieben werden:
- \[L_{\rm E}(i) = 2 \cdot {\rm tanh}^{-1} \hspace{0.1cm} \left [ \prod\limits_{j \ne i}^{n} \hspace{0.15cm}{\rm tanh}(L_j/2) \right ] \hspace{0.3cm}{\rm mit}\hspace{0.3cm}L_j = L_{\rm APP}(j) \hspace{0.05cm}.\]
$\text{Beispiel 6:}$ Wir gehen vom Single Parity–check Code mit $n = 3, \ k = 2$ ⇒ kurz ${\rm SPC} \ (3, \ 2, \ 2)$ aus. Die $2^k = 4$ gültigen Codeworte $\underline{x} = \{x_1, x_2, x_3\}$ lauten bei bipolarer Beschreibung ⇒ $x_i ∈ \{±1\}$:
- $$ \underline{x}_0 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm}+1\hspace{-0.03cm},\hspace{-0.05cm}+1)\hspace{-0.05cm}, $$
- $$\underline{x}_1 \hspace{-0.05cm}=\hspace{-0.05cm} (+1\hspace{-0.03cm},\hspace{-0.05cm} -1\hspace{-0.03cm},\hspace{-0.05cm} -1)\hspace{-0.05cm}, $$
- $$\underline{x}_2 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm} +1\hspace{-0.03cm},\hspace{-0.05cm} -1)\hspace{-0.05cm}, $$
- $$\underline{x}_3 \hspace{-0.05cm}=\hspace{-0.05cm} (-1\hspace{-0.03cm},\hspace{-0.05cm} -1\hspace{-0.03cm},\hspace{-0.05cm} +1)\hspace{-0.05cm}. $$
Bei diesem Code ist also das Produkt $x_1 \cdot x_2 \cdot x_3$ stets positiv.
Die obige Tabelle zeigt den Decodiervorgang für $\underline{L}_{\rm APP} = (+2.0, +0.4, \, –1.6)$. Die harte Entscheidung nach den Vorzeichen von $L_{\rm APP}(i)$ ergäbe hier $(+1, +1, \, –1)$, also kein gültiges Codewort des ${\rm SP}(3, \ 2, \ 2)$.
Rechts sind in der Tabelle die dazugehörigen extrinsischen $L$–Werte eingetragen:
- \[L_{\rm E}(1) = 2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh} (0.2) \cdot {\rm tanh} (-0.8)\hspace{0.05cm}\right ] = -0.131\hspace{0.05cm}, \]
- \[L_{\rm E}(2) =2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh} (1.0) \cdot {\rm tanh} (-0.8)\hspace{0.05cm}\right ] = -0.518\hspace{0.05cm}, \]
- \[L_{\rm E}(3) =2 \cdot {\rm tanh}^{-1} \hspace{0.05cm} \left [ {\rm tanh} (1.0) \cdot {\rm tanh} (0.2)\hspace{0.05cm}\right ] = +0.151\hspace{0.05cm}.\]
Die zweite Gleichung lässt sich wie folgt interpretieren:
- $L_{\rm APP}(1) = +2.0$ und $L_{\rm APP}(3) = \, –1.6$ sagen aus, dass das erste Biteher „$+1$” als „$-1$” ist und das dritte Bit eher „$-1$” als „$+1$”. Die Zuverlässigkeit (Betrag) ist beim ersten Bit etwas größer als beim dritten.
- Die extrinsische Information $L_{\rm E}(2) = \, –0.518$ berücksichtigt nur die Informationen von Bit 1 und Bit 3 über Bit 2. Aus deren Sicht ist das zweite Bit eine „$-1$” mit der Zuverlässigkeit $0.518$.
- Der vom Empfangswert $y_2$ abgeleitete $L$–Wert ⇒ $L_{\rm APP}(2) = +0.4$ hat für das zweite Bit eine „$+1$” vermuten lassen. Die Diskrepanz wird hier bereits in der Iteration $I = 1$ aufgelöst.
- Entschieden wird hier für das Codewort $\underline{x}_1$. Bei $0.518 < L_{\rm APP}(2) < 1.6$ würde das Ergebnis $\underline{x}_1$ erst nach mehreren Iterationen vorliegen. Für $L_{\rm APP}(2) > 1.6$ liefert der Decoder dagegen $\underline{x}_0$.
BCJR–Decodierung: Vorwärts–Rückwärts–Algorithmus
Ein Beispiel für die iterative Decodierung von Faltungscodes ist der BCJR–Algorithmus, benannt nach dessen Erfindern L. R. Bahl, J. Cocke, F. Jelinek und J. Raviv ⇒ [BCJR74][2]. Der Algorithmus weist viele Parallelen zur sieben Jahren älteren Viterbi–Decodierung auf, doch auch einigesignifikante Unterschiede:
- Während Viterbi die Gesamtsequenz schätzt ⇒ block–wise Maximum Likelihood, minimiert der BCJR–Algorithmus die Bitfehlerwahrscheinlichkeit ⇒ bit–wise MAP.
- Der Viterbi–Algorithmus kann (in seiner ursprünglichen Form) keine Softinformation verarbeiten. Dagegen gibt der BCJR–Algorithmus bei jeder Iteration für jedes einzelne Symbol (Bit) einen Zuverlässigkeitswert an, der bei späteren Iterationen berücksichtigt wird.
Die Abbildung soll – fast unzulässig vereinfacht – die unterschiedliche Vorgehensweise von Viterbi–Algorithmus (links) und BCJR–Algorithmus (rechts) verdeutlichen. Zugrunde liegt ein Faltungscode mit dem Gedächtnis $m = 1$ und der Länge $L = 4$ ⇒ Gesamtlänge (mit Terminierung) $L' = 5$.
- Der Viterbi–Algorithmus sucht und findet den wahrscheinlichsten Pfad von ${\it \Gamma}_0(S_0)$ nach ${\it \Gamma}_5(S_0)$, nämlich $S_0 → S_1 → S_0 → S_0 → S_1→ S_0 $. Wir verweisen auf die Musterlösung zur Aufgabe 3.9Z.
Die Skizze für den BCJR–Algorithmus verdeutlicht die Gewinnung des extrinsischen $L$–Wertes für das dritte Symbol ⇒ $L_{\rm E}(3)$. Der relevante Bereich im Trellis ist schraffiert:
- Bei der Abarbeitung des Trellisdiagramms in Vorwärtsrichtung gewinnt man – in gleicher Weise wie bei Viterbi – die Metriken $\alpha_1, \ \alpha_2, \ \text{...}\hspace{0.05cm} , \ \alpha_5$. Zur Berechnung von $L_{\rm E}(3)$ benötigt man hiervon $\alpha_2$.
- Anschließend durchläuft man das Trellisdiagramm rückwärts (also von rechts nach links) und erhält damit die Metriken $\beta_4, \ \beta_3, \ \text{...}\hspace{0.05cm} , \ \beta_0$ entsprechend der unteren Skizze.
- Der gesuchte extrinsische $L$–Wert $L_{\rm E}(3)$ ergibt sich aus den Metriken $\alpha_2$ (in Vorwärtsrichtung) und $\beta_3$ (in Rückwärtsrichtung) sowie der Apriori–Information $\gamma_3$ über das Symbol $i = 3$.
Grundstruktur von verketteten Codiersystemen
Die wichtigsten Kommunikationssysteme der letzten Jahre verwenden zwei unterschiedliche Kanalcodes. Man spricht dann von verketteten Codiersystemen (englisch: Concatenated Codes). Auch bei relativ kurzen Komponentencodes $\mathcal{C}_1$ und $\mathcal{C}_2$ ergibt sich für den verketteten Code $\mathcal{C}$ eine hinreichend große Codewortlänge $n$, die ja bekanntlich erforderlich ist, um sich der Kanalkapazität anzunähern.
Zunächst seien einige Beispiele aus dem Mobilfunk genannt:
- Bei GSM (Global System for Mobile Communications, zweite Mobilfunkgeneration) wird zunächst die Datenbitrate von $9.6 \ \rm kbit/s$ auf $12 \ \rm kbit/s$ erhöht, um auch in leitungsvermittelten Netzen eine Fehlererkennung zu ermöglichen. Anschließend folgt ein punktierter Faltungscode mit der Ausgangsbitrate $22.8 \ \rm kbit/s$. Die Gesamtcoderate beträgt somit etwa $42.1\%$.
- Beim 3G–Mobilfunksystem UMTS (Universal Mobile Telecommunications System) verwendet man je nach den Randbedingungen (guter/schlechter Kanal, wenige/viele Teilnehmer in der Zelle) einen Faltungscode oder einen Turbocode (darunter versteht man per se die Verkettung zweier Faltungscodierer). Beim 4G–Mobilfunksystem LTE (Long Term Evolution) verwendet man für kurze Kontrollsignale einen Faltungscode und für die längeren Payload-Daten einen Turbocode.
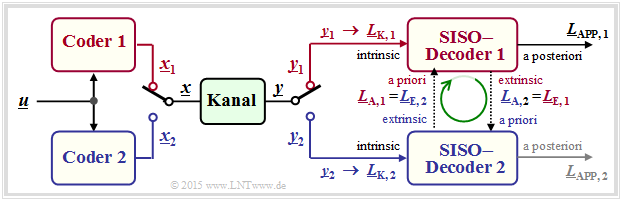
Die Grafik zeigt die Grundstruktur eines parallel verketteten Codiersystems. Alle Vektoren bestehen aus $n$ Elementen: $\underline{L} = (L(1), \ \text{...}\hspace{0.05cm} , \ L(n))$. Die Berechnung aller $L$–Werte geschieht also auf Symbolebene. Nicht dargestellt ist hier der Interleaver, der zum Beispiel bei den Turbocodes obligatorisch ist.
- Die Codesequenzen $\underline{x}_1$ und $\underline{x}_2$ werden zur gemeinsamen Übertragung über den Kanal durch einen Multiplexer zum Vektor $\underline{x}$ zusammengefügt. Am Empfänger wird die Sequenz $\underline{y}$ wieder in die Einzelteile $\underline{y}_1$ und $\underline{y}_2$ zerlegt. Daraus werden die Kanal–$L$–Werte $\underline{L}_{\rm K,\hspace{0.05cm}1}$ und $\underline{L}_{K,\hspace{0.05cm}2}$ gebildet.
- Der symbolweise Decoder ermittelt entsprechend der vorne beschriebenen Vorgehensweise die extrinsischen $L$–Werte $\underline{L}_{\rm E,\hspace{0.05cm} 1}$ und $\underline{L}_{E,\hspace{0.05cm} 2}$, die gleichzeitig die Apriori–Informationen $\underline{L}_{\rm A,\hspace{0.05cm} 2}$ und $\underline{L}_{\rm A,\hspace{0.05cm} 1}$ für den jeweils anderen Decoder darstellen.
- Nach ausreichend vielen Iterationen (also dann, wenn ein Abbruchkriterium erfüllt ist) liegt am Decoderausgang der Vektor der Aposteriori–Werte ⇒ $\underline{L}_{\rm APP}$ an. Im Beispiel wird willkürlich der Wert im oberen Zweig genommen. Möglich wäre aber auch der untere $L$–Wert.
Das obige Modell gilt insbesondere auch für die Decodierung der Turbo–Codes gemäß dem Kapitel Grundlegendes zu den Turbocodes.
Aufgaben zum Kapitel
Aufgabe 4.1: Zum „Log Likelihood Ratio”
Aufgabe 4.1Z: L–Werte des BEC–Modells
Aufgabe 4.2: Kanal–LLR bei AWGN
Aufgabe 4.3: Iterative Decodierung beim BSC
Aufgabe 4.3Z: Umrechnungen von L–Wert und S–Wert
Aufgabe 4.4: Extrinsische L–Werte beim SPC
Aufgabe 4.4Z: Ergänzung zur Aufgabe 4.4
Aufgabe 4.5: Nochmals zu den extrinsischen L–Werten
Aufgabe 4.5Z: Tangens Hyperbolikus und Inverse
Quellenverzeichnis