Exercise 4.07: Decision Boundaries once again

• Return to book

WDF mit ungleichen Symbolwahrscheinlichkeiten

Wir betrachten ein Übertragungssystem mit

• nur einer Basisfunktino  $(N = 1)$,
• zwei Signalen  $(M = 2)$  mit  $s_0 = \sqrt{E_s}$  und  $s_1 = -\sqrt{E_s}$ ,
• einem AWGN–Kanal mit Varianz  $\sigma_n^2 = N_0/2$.

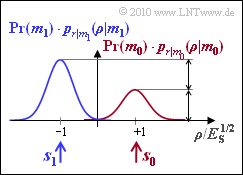
Da in dieser Aufgabe der allgemeine Fall  ${\rm Pr}(m_0) ≠ {\rm Pr}(m_1)$  behandelt wird, genügt es nicht, die bedingten Dichtefunktionen  $p_{\it r\hspace{0.05cm}|\hspace{0.05cm}m_i}(\rho\hspace{0.05cm} |\hspace{0.05cm}m_i)$  zu betrachten. Vielmehr müssen diese noch mit den Symbolwahrscheinlichkeiten  ${\rm Pr}(m_i)$  multipliziert werden. Für  $i$  sind hier die Werte  $0$  und  $1$  einzusetzen.

Liegt die Entscheidungsgrenze zwischen den beiden Regionen  $I_0$  und  $I_1$  bei  $G = 0$, also in der Mitte zwischen  $\boldsymbol{s}_0$  und  $\boldsymbol{s}_1$, so ist die Fehlerwahrscheinlichkeit unabhängig von den Auftrittswahrscheinlichkeiten  ${\rm Pr}(m_0)$  und  ${\rm Pr}(m_1)$:

$$p_{\rm S} = {\rm Pr}({ \cal E} ) = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right ) \hspace{0.05cm}.$$

Hierbei gibt  $d$  den Abstand zwischen den Signalpunkten  $s_0$  und  $s_1$  an und  $d/2$  dementsprechend den jeweiligen Abstand von  $s_0$  bzw.  $s_1$  von der Entscheidungsgrenze  $G = 0$. Der Effektivwert (Wurzel aus der Varianz) des AWGN–Rauschens ist  $\sigma_n$.

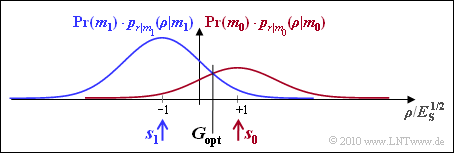
Sind dagegen die Auftrittswahrscheinlichkeiten unterschiedlich   ⇒  ${\rm Pr}(m_0) ≠ {\rm Pr}(m_1)$, so kann durch eine Verschiebung der Entscheidergrenze  $G$  eine kleinere Fehlerwahrscheinlichkeit erzielt werden:

$$p_{\rm S} = {\rm Pr}(m_1) \cdot {\rm Q} \left ( \frac{d/2}{\sigma_n} \cdot (1 + \gamma) \right ) + {\rm Pr}(m_0) \cdot {\rm Q} \left ( \frac{d/2}{\sigma_n} \cdot (1 - \gamma) \right )\hspace{0.05cm},$$

wobei die Hilfsgröße  $\gamma$  wie folgt definiert ist:

$$\gamma = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_1)}{{\rm Pr}( m_0)} \hspace{0.05cm},\hspace{0.2cm} G_{\rm opt} = \gamma \cdot \sqrt {E_{\rm S}}\hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel  Approximation der Fehlerwahrscheinlichkeit.

• Die Werte der Q–Funktion können Sie mit interaktiven Applet  Komplementäre Gaußsche Fehlerfunktion  ermitteln.

Fragebogen

1

Wie groß sind die der Grafik zugrundeliegenden Symbolwahrscheinlichkeiten, wenn die blaue Gaußkurve genau doppelt so hoch ist wie die rote?

${\rm Pr}(m_0)\ = \ $

${\rm Pr}(m_1)\ = \ $

2

Wie groß ist die Fehlerwahrscheinlichkeit mit der Rauschvarianz  $\sigma_n^2 = E_{\rm S}/9$  und der vorgegebenen Schwelle  $G = 0$?

$G = 0 \text{:} \hspace{0.85cm} p_{\rm S} \ = \ $ $\ \%$

3

Wie lautet die optimale Schwelle für die gegebenen Wahrscheinlichkeiten?

$G_{\rm opt}\ = \ $ $\ \cdot \sqrt{E_s}$

4

Wie groß ist die Fehlerwahrscheinlichkeit bei optimaler Schwelle  $G = G_{\rm opt}$?

$G = G_{\rm opt} \text{:} \hspace{0.2cm} p_{\rm S}\ = \ $ $\ \%$

5

Welche Fehlerwahrscheinlichkeiten erhält man mit der Rauschvarianz  $\sigma_n^2 = E_{\rm S}$?

$G = 0 \text{:} \hspace{0.85cm} p_{\rm S}\ = \ $ $\ \%$

$G = G_{\rm opt} \text{:} \hspace{0.2cm} p_{\rm S}\ = \ $ $\ \%$

6

Welche Aussagen gelten für die Rauschvarianz  $\sigma_n^2 = 4 \cdot E_{\rm S}$?

	Mit  $G = 0$  ist die Fehlerwahrscheinlichkeit größer als  $30\%$.
	Die optimale Entscheiderschwelle liegt rechts von  $s_0$.
	Bei optimaler Schwelle ist die Fehlerwahrscheinlichkeit etwa  $27\%$.
	Der Schätzwert  $m_0$  ist nur mit genügend großem Rauschen möglich.

Musterlösung

Solution

(1)  Die Höhen der beiden gezeichneten Dichtefunktionen sind proportional zu den Auftrittswahrscheinlichkeiten ${\rm Pr}(m_0)$ und ${\rm Pr}(m_1)$. Aus

$${\rm Pr}(m_1) = 2 \cdot {\rm Pr}(m_0) \hspace{0.05cm},\hspace{0.2cm} {\rm Pr}(m_0) + {\rm Pr}(m_1) = 1$$

folgt direkt  ${\rm Pr}(m_0) = 1/3 \ \underline {\approx 0.333}$  und  ${\rm Pr}(m_1) = 2/3 \ \underline {\approx 0.667}$.

(2)  Mit der Entscheidergrenze $G = 0$ gilt unabhängig von den Auftrittswahrscheinlichkeiten:

$$p_{\rm S} = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right ) \hspace{0.05cm}.$$

Mit $d = 2 \cdot \sqrt{E_{\rm S}}$ und $\sigma_n = \sqrt{E_{\rm S}}/3$ ergibt sich hierfür:   $p_{\rm S} = {\rm Q} (3) \hspace{0.1cm} \hspace{0.15cm}\underline {\approx 0.135 \%} \hspace{0.05cm}.$

(3)  Entsprechend der Angabe gilt für den „normierten Schwellenwert”:

$$\gamma = \frac{G_{\rm opt}}{E_{\rm S}^{1/2}} = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_1)}{{\rm Pr}( m_0)} = \frac{ 2 \cdot E_{\rm S}/9}{4 \cdot E_{\rm S}} \cdot {\rm ln} \hspace{0.15cm} \frac{2/3}{1/3} \hspace{0.1cm}\hspace{0.15cm}\underline {\approx 0.04} \hspace{0.05cm}.$$

• Damit ist $G_{\rm opt} = \gamma \cdot \sqrt{E_{\rm S}} = 0.04 \cdot \sqrt{E_{\rm S}}$.
• Die optimale Entscheidergrenze ist demnach nach rechts (hin zum unwahrscheinlicheren Symbol $s_0$) verschoben, wgen  ${\rm Pr}(m_0) < {\rm Pr}(m_1)$.

(4)  Mit dieser optimalen Entscheidergrenze ergibt sich eine gegenüber der Teilaufgabe (2) geringfügig kleinere Fehlerwahrscheinlichkeit:

$$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {2}/{3} \cdot {\rm Q} (3 \cdot 1.04) + {1}/{3} \cdot {\rm Q} (3 \cdot 0.96) = {2}/{3} \cdot 0.090 \cdot 10^{-2} + {1}/{3} \cdot 0.199 \cdot 10^{-2} \hspace{0.1cm}\hspace{0.15cm}\underline {\approx 0.126 \%} \hspace{0.05cm}.$$

(5)  Mit der Entscheidergrenze in der Mitte zwischen den Symbolen ($G = 0$) ergibt sich analog zur Teilaufgabe (2) mit der nun größeren Rauschvarianz:

Dichtefunktionen mit  $\sigma_n^2 = E_{\rm S}$

$$p_{\rm S} = {\rm Q} \left ( \frac{d/2}{\sigma_n} \right ) = {\rm Q} \left ( \frac{\sqrt{E_{\rm S}}}{\sqrt{E_{\rm S}}} \right )= {\rm Q} (1)\hspace{0.1cm} \hspace{0.15cm}\underline {\approx 15.9 \%} \hspace{0.05cm}.$$

Die Kenngröße $\gamma$ (normierte bestmögliche Verschiebung der Entscheidergrenze) ist

$$\gamma = 2 \cdot \frac{ \sigma_n^2}{d^2} \cdot {\rm ln} \hspace{0.15cm} \frac{{\rm Pr}( m_1)}{{\rm Pr}( m_0)} = \frac{ 2 \cdot E_{\rm S}}{4 \cdot E_{\rm S}} \cdot {\rm ln} \hspace{0.15cm} \frac{2/3}{1/3} = \frac{{\rm ln} \hspace{0.15cm} 2}{2} \approx 0.35$$

$$\Rightarrow \hspace{0.3cm} G_{\rm opt} = 0.35 \cdot \sqrt{E_{\rm S}} \hspace{0.05cm}.$$

Das häufigere Symbol wird nun seltener verfälscht ⇒ die mittlere Fehlerwahrscheinlichkeit wird geringer:

$$p_{\rm S} = {2}/{3} \cdot {\rm Q} (1.35) + {1}/{3} \cdot {\rm Q} (0.65) = {2}/{3} \cdot 0.0885 +{1}/{3} \cdot 0.258 \hspace{0.1cm} \hspace{0.15cm}\underline {\approx 14.5 \%} \hspace{0.05cm}.$$

Die Abbildung macht deutlich, dass die optimale Entscheidergrenze auch grafisch als Schnittpunkt der beiden (gewichteten) Wahrscheinlichkeitsdichtefunktionen ermittelt werden kann:

(6)  Alle Lösungsvorschläge dieser eher akademischen Teilaufgabe sind richtig:

Dichtefunktionen mit  $\sigma_n^2 = 4 \cdot E_{\rm S}$

• Mit dem Schwellenwert $G = 0$ ergibt sich $p_{\rm S} = {\rm Q}(0.5) \ \underline {\approx 0.309}$.
• Die Kenngröße $\gamma = 1.4$ hat nun den vierfachen Wert gegenüber der Teilaufgabe (5),
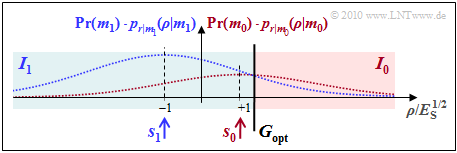
  so dass die optimale Entscheidergrenze nun bei $G_{\rm opt} = \underline {1.4 \cdot s_0}$ liegt.
• Somit gehört der (ungestörte) Signalwert $s_0$ nicht zur Entscheidungsregion $I_0$, sondern zu $I_1$, gekennzeichnet durch $\rho < G_{\rm opt}$.
• Nur mit einem (positiven) Rauschanteil ist $I_0 (\rho > G_{\rm opt})$ überhaupt erst möglich. Für die Fehlerwahrscheinlichkeit gilt mit $G_{\rm opt} = 1.4 \cdot s_0$:

$$p_{\rm S} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {2}/{3} \cdot {\rm Q} (0.5 \cdot (1 + 1.4)) + {1}/{3} \cdot {\rm Q} (0.5 \cdot (1 - 1.4)) = \hspace{0.15cm}\underline {\approx 27\%} \hspace{0.05cm}.$$

Die nebenstehende Grafik verdeutlicht die hier gemachten Aussagen.