The Fourier Transform Theorems

Multiplikation mit Faktor - Additionssatz

In diesem Abschnitt sind die Gesetzmäßigkeiten der Fouriertransformation zusammengestellt. Diese können beispielsweise dazu genutzt werden, um mit möglichst geringem Rechenaufwand aus bereits bekannten Transformationen

$x( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X( f ),\quad x_1 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_1 ( f ),\quad x_2 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_2 ( f )$

neue Funktionszusammenhänge abzuleiten. Wir beschränken uns hier auf reelle Zeitfunktionen.

$\text{Satz:}$ Ein konstanter Faktor $k$ wirkt sich auf die Zeit– und die Spektralfunktion in gleicher Weise aus:

$k \cdot x(t)\ \;\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ k \cdot X(f).$

Diesen Zusammenhang kann man zum Beispiel zur Vereinfachung nutzen, indem man die Konstante $k$ (die sowohl ein Verstärkungs–, ein Dämpfungs- oder ein Einheitenfaktor sein kann) zunächst weglässt und erst später dem Ergebnis wieder hinzufügt.

Obiger Satz folgt unmittelbar aus der Definition des ersten Fourierintegrals, ebenso wie der Additionssatz, der die Grundlage für das Superpositionsprinzip darstellt.

$\text{Additionssatz:}$ Kann man eine Zeitfunktion als Summe von Einzelfunktionen schreiben, so ist die resultierende Spektralfunktion die Summe der resultierenden Einzelspektren:

$x( t ) = x_1 ( t ) + x_2 ( t )\quad\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad X( f ) = X_1 (f) + X_2 ( f ).$

Rechteckimpuls, Dreieckimpuls und Kombination

$\text{Beispiel 1:}$ Bekannt sind die Fourierkorrespondenzen

des Rechtecksignals:

$x_1 ( t )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X_1 ( f )=T \cdot {\rm si}(\pi f T),$

des Dreiecksignals:

$x_2 ( t )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X_2 ( f )=T /2\cdot {\rm si}(\pi f T/2).$

Diese beiden impulsförmigen Signale sind als rote bzw. blaue Kurve skizziert.

Dann gilt für das grün gezeichnete (gewichtete) Summensignal:

$x(t) = {1}/{3} \cdot x_1 ( t ) + {2}/{3} \cdot x_2 ( t )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X(f) = {1}/{3} \cdot X_1 ( f ) + {2}/{3} \cdot X_2 ( f ).$

Hinweis: Alle in diesem Kapitel dargelegten Gesetzmäßigkeiten werden im Lernvideo Gesetzmäßigkeiten der Fouriertransformation an Beispielen verdeutlicht.

Zuordnungssatz

Bereits bei der komplexen Fourierreihe zur Beschreibung periodischer Signale haben wir festgestellt, dass eine gerade Funktion stets zu reellen und eine ungerade Funktion ausschließlich zu imaginären Fourierkoeffizienten führt. Die Fouriertransformation zeigt ähnliche Eigenschaften.

$\text{Zuordnungssatz:}$ Besteht eine reelle Zeitfunktion additiv aus einem geraden und einem ungeraden Anteil,

$x( t ) = x_{\rm g} ( t ) + x_{\rm u} ( t ),$

so gilt für die dazugehörige Spektralfunktion:

$X(f) = X_{\rm R}(f) + {\rm j}\cdot X_{\rm I}(f), \hspace{0.5cm}\text{mit}$

$x_{\rm g} (t) \hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X_{\rm R}(f),$

$x_{\rm u} (t) \hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} {\rm j} \cdot X_{\rm I} (f).$

Der Realteil $X_{\rm R}(f)$ des Spektrums ist dann ebenfalls gerade, während $X_{\rm I}(f)$ eine ungerade Funktion der Frequenz beschreibt.

Der Zuordnungssatz lässt sich einfach beweisen, wenn man den Satz von Leonhard Euler ⇒ ${\rm e}^{ - {\rm j}\omega _0 t} = \cos ( {\omega _0 t} ) - {\rm j}\cdot \sin ( {\omega _0 t} )$ berücksichtigt. Den geraden und ungeraden Anteil einer Funktion $x(t)$ kann man mit folgenden Gleichungen berechnen:

$x_{\rm g} (t) = {1}/{2}\big[ {x(t) + x(-t)} \big],$

$x_{\rm u} (t) = {1}/{2}\big[ {x(t) - x(-t)} \big].$

Spektrum der Sprungfunktion

$\text{Beispiel 2:}$ Wir betrachten die Sprungfunktion

$x(t) = \gamma (t) = \bigg\{ \begin{array}{l} 0\quad \quad {\rm f\ddot{u} r}\;t < 0 \\ 1\quad \quad{\rm f\ddot{u} r}\; t > 0 \\ \end{array} ,$

die wie folgt aufgeteilt werden kann:

$\gamma (t) = {1}/{2} +{1}/{2} \cdot {\rm sign}(t).$

Hierbei wurde die Signum-Funktion verwendet:

${\rm sign} (t) = \bigg\{ \begin{array}{l} -1\quad \quad {\rm f\ddot{u} r}\;t < 0, \\ +1\quad \quad{\rm f\ddot{u} r}\; t > 0. \\ \end{array}$

Somit gilt:

Der gerade (blaue) Signalanteil $x_{\rm g} (t) = {1}/{2}$ ist eine Konstante mit der reellen Spektralfunktion $X_{\rm R}(f) = {1}/{2} \cdot \delta(f)$ .
Das Spektrum ${\rm j} \cdot X_{\rm I}(f)$ der ungeraden (grünen) Signumfunktion $x_{\rm u} (t)$ wurde bereits im früheren $\text{Beispiel 3}$ auf der Seite „Fouriertransformation” berechnet.
Damit erhält man für das resultierende Spektrum der rot skizzierten Sprungfunktion $x(t) = \gamma (t)$ :

$X(f) = X_{\rm R}(f) + {\rm j}\cdot X_{\rm I}(f)= {1}/{2} \cdot \delta (f) - {\rm j}\cdot \frac{1}{2\pi f}.$

Ähnlichkeitssatz

Der Ähnlichkeitssatz zeigt den Zusammenhang zwischen den Spektralfunktionen zweier zwar formgleicher, aber gestreckter oder gestauchter Zeitsignale auf.

$\text{Ähnlichkeitssatz:}$ Ist $X(f)$ die Fouriertransformierte von $x(t)$ , so gilt mit der reellen Konstanten $k$ auch folgenderZusammenhang:

$x( {k \cdot t} )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} \frac{1}{\left \vert k \right \vert} \cdot X( {f}/{k} ).$

$\text{Beweis:}$ Für positives $k$ folgt aus dem Fourierintegral mit der Substitution $\tau = k \cdot t$ :

$\int_{ - \infty }^{ + \infty } {x( {k \cdot t})} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}ft} \hspace{0.1cm}{\rm d}t = \frac{1}{k} \cdot \int_{ - \infty }^{ + \infty } {x( \tau )} \cdot {\rm e}^{ - {\rm j}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm} f/k \hspace{0.05cm}\cdot \hspace{0.05cm}\tau } \hspace{0.1cm}{\rm d} \tau = \frac{1}{k}\cdot X( {{f}/{k}}).$

Für negatives $k$ würden sich die Integrationsgrenzen vertauschen und man erhält $-1/k \cdot X(f/k)$ .
Da in der Gleichung $\vert k \vert$ verwendet wird, gilt das Ergebnis für beide Vorzeichen.

q.e.d.

Die Auswirkungen des Ähnlichkeitssatzes kann man sich zum Beispiel mit einem Tonband verdeutlichen. Spielt man ein solches Band mit doppelter Geschwindigkeit ab, so entspricht dies einer Stauchung des Zeitsignals $(k = 2)$ . Dadurch erscheinen die Frequenzen doppelt so hoch.

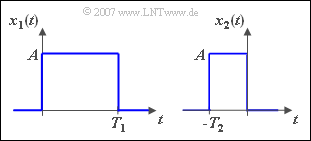
Zwei Rechtecke unterschiedlicher Breite

$\text{Beispiel 3:}$ Wir betrachten zwei Rechtecke gleicher Höhe, wobei $T_2 = T_1/2$ gilt.

Die Spektralfunktion von $x_1(t)$ ergibt sich nach dem ersten Fourierintegral zu

$X_1 (f) = A \cdot \frac{ {1 - {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } } }{ { {\rm j}2\pi f} } .$

Dafür kann auch geschrieben werden:

$X_1 (f) = A \cdot T_1 \cdot \frac{{{\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } - {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } }}{{{\rm j}2\pi fT_1 }} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } = A \cdot T_1 \cdot {\rm si}( {\pi f T_1 } ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 }.$

Für die Spektralfunktion von $x_2(t)$ folgt aus dem Ähnlichkeitssatz mit $k = -2$ :

$X_2 (f) = \frac{1}{2} \cdot X_1 ( { - {f}/{2}} ) = \frac{A \cdot T_1 }{2} \cdot {\rm si}( { - \pi f {T_1 }/{2} } ) \cdot {\rm e}^{ {\rm j}\pi fT_1 /2} .$

Die $\text{si}$ –Funktion ist gerade: $\text{si}(-x) = \text{si}(x)$ . Deshalb kann man auf das Vorzeichen im Argument der $\text{si}$ –Funktion verzichten.

Mit $T_2 = T_1/2$ erhält man schließlich:

$X_2 (f) = A \cdot T_2 \cdot {\rm si}( {\pi fT_2 } ) \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_2 } .$

Reziprozitätsgesetz von Zeitdauer und Bandbreite

Dieses Gesetz folgt direkt aus dem Ähnlichkeitssatz: Je breiter ein Impuls in seiner Ausdehnung ist, desto schmäler und höher ist das zugehörige Spektrum und umgekehrt.

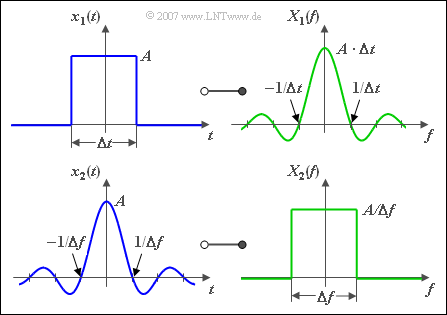
Um quantitative Aussagen treffen zu können, definieren wir zwei Kenngrößen für energiebegrenzte Signale ⇒ Impulse. Beide Größen werden sind in der Grafik zum $\text{Beispiel 4}$ für einen Gaußimpuls und dessen ebenfalls gaußförmiges Spektrum dargestellt.

$\text{Definition:}$ Die äquivalente Impulsdauer wird aus dem Zeitverlauf abgeleitet. Sie ist gleich der Breite eines flächengleichen Rechtecks mit gleicher Höhe wie $x(t)$ :

$\Delta t = \frac{1}{{x( {t = 0} )}} \cdot \int_{ - \infty }^{ + \infty } {x( t)} \hspace{0.1cm}{\rm d}t.$

$\text{Definition:}$ Die äquivalente Bandbreite kennzeichnet den Impuls im Frequenzbereich. Sie gibt die Breite des flächengleichen Rechtecks mit gleicher Höhe wie das Spektrum $X(f)$ an:

$\Delta f = \frac{1}{{X( {f = 0} )}}\cdot \int_{ - \infty }^{ + \infty } {X( f )} \hspace{0.1cm} {\rm d}f.$

$\text{Reziprozitätsgesetz:}$ Das Produkt aus äquivalenter Impulsdauer und äquivalenter Bandbreite ist stets gleich $1$ :

$\Delta t \cdot \Delta f = 1$

$\text{Beweis:}$ Ausgehend von den beiden Fourierintegralen erhält man für $f = 0$ bzw. $t = 0$ :

$X( {f = 0} ) = \int_{ - \infty }^{ + \infty } {x(t)\hspace{0.1cm}{\rm d}t,} \hspace{0.5cm}x( {t = 0} ) = \int_{ - \infty }^{ + \infty } {X(f)\hspace{0.1cm}{\rm d}f.}$

Berücksichtigt man dieses Ergebnis bei obigen Definitionen, so erhält man:

$\Delta t = \frac{{X( {f = 0} )}}{{x( {t = 0} )}}, \hspace{0.5cm}\Delta f = \frac{{x( {t = 0} )}}{{X( {f = 0} )}}.$

Daraus folgt direkt

$\Delta t \cdot \Delta f = 1$ .

q.e.d.

Anzumerken ist, dass $\Delta f$ über das tatsächliche Spektrum $X(f)$ und nicht über $|X(f)|$ definiert ist.

Bei reellen Funktionen genügt die Integration über den geraden Funktionsanteil, da das Integral über den ungeraden Anteil wegen des Zuordnungssatzes stets Null ist.
Bei ungeraden Zeitfunktionen und damit rein imaginären Spektren versagen die beiden Definitionen von $\Delta t$ bzw. $\Delta f$ .

Gauß–Beispiel zum Reziprozitätsgesetz

$\text{Beispiel 4:}$ Die Grafik verdeutlicht die äquivalente Impulsdauer $\Delta t$ und die äquivalente Bandbreite $\Delta f$ beispielhaft für den Gaußimpuls. Weiter gilt:

Verbreitert man den Gaußimpuls um den Faktor $3$ , so wird die äquivalente Bandbreite um den gleichen Faktor kleiner.
Wenn hierbei die Impulsamplitude $x(t = 0)$ nicht verändert wird, bleibt auch die Integralfläche über $X(f)$ konstant.
Das heißt, dass $X(f=0)$ gleichzeitig um den Faktor $3$ größer wird.

Vertauschungssatz

Diese Gesetzmäßigkeit ist besonders nützlich, um neue Fourierkorrespondenzen zu erhalten.

$\text{Vertauschungssatz:}$ Ist $X(f)$ die Fouriertransformierte von $x(t)$ , dann gilt auch:

$X^{\star}(t)\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}x^{\star}( f ).$

Beschränken wir uns auf reelle Zeitfunktionen, so können die Zeichen für „konjugiert komplex” auf beiden Seiten der Fourierkorrespondenz weggelassen werden.

$\text{Beweis:}$ Das erste Fourierintegral lautet nach sukzessiver Umbenennung $t \to u$ bzw. $f \to t$ :

$X( f ) = \int_{ - \infty }^{ + \infty } {x( u )} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}u} \hspace{0.1cm}{\rm d}u, \hspace{1cm} X(t ) = \int_{ - \infty }^{ + \infty } {x( u )} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}t\hspace{0.05cm}\cdot \hspace{0.05cm}u}\hspace{0.1cm} {\rm d}u.$

Ändert man das Vorzeichen in den Exponenten, so muss man $X(t)$ durch $X^*(t)$ und $x(u)$ durch $x^*(u)$ ersetzen:

$X^{\star}(t ) = \int_{ - \infty }^{ + \infty } {x^{\star}( u )} \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi\hspace{0.05cm}\cdot \hspace{0.05cm} t\hspace{0.05cm}\cdot \hspace{0.05cm}u}\hspace{0.1cm} {\rm d}u.$

Mit der weiteren Umbennung $u \to f$ kommt man zum zweiten Fourierintegral:

$X^{\star}(t ) = \int_{ - \infty }^{ + \infty } {x^{\star}( f )} \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}f.\hspace{7.9cm}$

q.e.d.

Rechteck

$\ \leftrightarrow \ \ \rm si$ –Funktion

$\text{Beispiel 5:}$ Das Spektrum $X(f) = \delta(f)$ des Gleichsignals $x(t) = 1$ wird als bekannt vorausgesetzt.

Nach dem Vertauschungssatz lautet deshalb die Spektralfunktion des Diracimpulses $x(t) = \delta(t)$ :

$x(t) = \delta(t)\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X(f)= 1.$

Die Grafik zeigt eine weitere Anwendung des Vertauschungssatzes, nämlich die Funktionalzusammenhänge zwischen

einem Signal $x_1(t)$ mit rechteckförmiger Zeitfunktion, und
einem Signal $x_2(t)$ mit rechteckförmiger Spektralfunktion.

Verschiebungssatz

Wir betrachten nun eine Verschiebung der Zeitfunktion – zum Beispiel verursacht durch eine Laufzeit – oder eine Frequenzverschiebung, wie sie beispielsweise bei der (analogen) Zweiseitenband–Amplitudenmodulation auftritt.

$\text{Verschiebungssatz:}$ Ist $X(f)$ die Fouriertransformierte (Spektralfunktion) der Zeitfunktion $x(t)$ , so gelten auch folgende Zusammenhänge:

$\mathbf{(1)}\hspace{0.5cm}x( {t - t_0 } )\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X( f ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm} f\hspace{0.05cm}\cdot \hspace{0.05cm}t_0 },$

$\mathbf{(2)}\hspace{0.5cm}x( t ) \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_0 \hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X( {f - f_0 } ).$

Hierbei sind $t_0$ und $f_0$ beliebige Zeit– bzw. Frequenzgrößen.

$\text{Beweis von Gleichung (1):}$ Das erste Fourierintegral für das um $t_0$ nach rechts verschobene Signal $x_{\rm V}(t) = x(t-t_0)$ lautet mit der Substitution $\tau = t - t_0$ :

$X_{\rm V} ( f ) = \int_{ - \infty }^{ + \infty } {x( {t - t_0 } ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm}{\rm d}t} = \int_{ - \infty }^{ + \infty } {x( \tau ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}( {\tau + t_0 } )}\hspace{0.1cm} {\rm d}\tau .}$

Der von der Integrationsvariablen $\tau$ unabhängige Term kann vor das Integral gezogen werden. Mit der Umbennung $\tau \to t$ erhält man dann:

$X_{\rm V}( f ) = {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t_0 } \cdot \int_{ - \infty }^{ + \infty } {x( t )} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}t = {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t_0 } \cdot X( f).$

q.e.d.

Beispiel zum Verschiebungssatz

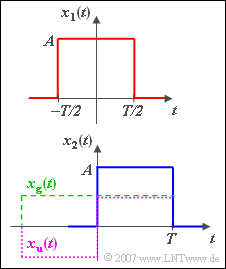
$\text{Beispiel 6:}$ Wie bereits erwähnt, besitzt der symmetrische Rechteckimpuls $x_1(t)$ das folgende Spektrum:

$X_1 ( f ) = A \cdot T \cdot {\rm si}( {\pi fT} ).$

Der unten dargestellte Rechteckimpuls $x_2(t)$ ist gegenüber $x_1(t)$ um $T/2$ nach rechts verschoben:

$x_2(t) = x_1(t-T/2).$

Somit lautet sein Spektrum:

$X_2( f ) = A \cdot T \cdot {\rm si}( {\pi fT} ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}T} .$

Diese Spektralfunktion kann mit dem Satz von Euler und einigen einfachen trigonometrischen Umformungen auch wie folgt geschrieben werden:

$X_2( f ) = \frac{A }{2\pi f} \cdot \sin ( 2\pi fT) + {\rm j}\cdot \frac{A }{2\pi f} \cdot \big[ {\cos ( {2\pi fT} ) - 1} \big] .$

Das gleiche Ergebnis erhält man auch mit dem Zuordnungssatz:

Der Realteil des Spektrums gehört zum geraden Signalanteil $x_{\rm g}(t)$ , der Imaginärteil zum ungeraden Anteil $x_{\rm u}(t)$ .

Differentiationssatz

Dieser Satz zeigt, wie sich die Differentiation einer Funktion $x(t)$ bzw. $X(f)$ in der korrespondierenden Fouriertransformierten auswirkt; er ist auch mehrfach anwendbar.

Ein einfaches Beispiel für die Anwendung des Differentiationsssatzes ist der Zusammenhang zwischen dem Strom $i(t)$ und der Spannung $u(t)$ einer Kapazität $C$ entsprechend der Gleichung $i(t) = C \cdot \text{d}u(t)/\text{d}t$ .

$\text{Differentiationsssatz:}$ Ist $X(f)$ die Fouriertransformierte von $x(t)$ , so gelten auch die beiden folgenden Korrespondenzen:

$\mathbf{(1)}\hspace{0.5cm}\frac{{{\rm d}x( t )}}{{{\rm d}t}}\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi f \cdot X( f ),$

$\mathbf{(2)}\hspace{0.5cm}- t \cdot x( t )\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}\frac{1}{{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi }} \cdot \frac{{{\rm d}X( f )}}{{{\rm d}f}}.$

$\text{Beweis von Gleichung (1):}$ Die erste Gleichung ergibt sich durch Differentiation des zweiten Fourierintegrals:

$y(t) = \frac{\text{d}x(t)}{\text{d}t} = \frac{\text{d} }{\text{d}t}\int_{ - \infty }^{ + \infty } X( f ) \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\hspace{0.03cm}\pi\hspace{0.05cm}\cdot \hspace{0.05cm} f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}f = \int_{ - \infty }^{ + \infty } {X( f )} \cdot {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi f \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm} f\hspace{0.05cm}\cdot \hspace{0.05cm}t} {\rm d}f.$

Gleichzeitig gilt aber auch:

$y( t ) = \int_{ - \infty }^{ + \infty } {Y( f )} \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\hspace{0.03cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}f.$

Durch Vergleich der Integranden erhält man die Variante $\mathbf{(1)}$ des Differentiationssatzes.
Zur Herleitung der zweiten Variante geht man ausgehend vom ersten Fourierintegral in analoger Weise vor.
Der negative Exponent im ersten Fourierintegral führt zum Minuszeichen in der Zeitfunktion.
q.e.d.

Zusammenhang Sprung

$\ \leftrightarrow \$ Dirac

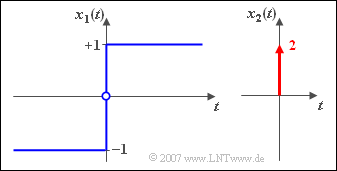
$\text{Beispiel 7:}$ Die Spektren der Signale $x_1(t)$ und $x_2(t)$ wurden bereits in früheren Beispielen wie folgt berechnet:

$X_1( f ) = \frac{1 }{ {\rm j\cdot \pi} f}, \hspace{1cm} X_2( f ) = 2 = {\rm const.}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} X_2(f) = X_1(f) \cdot {\rm j}\cdot 2\pi f.$

Aus dem Differentiationssatz folgt somit, dass $x_2(t)$ gleich der Ableitung von $x_1(t)$ nach der Zeit ist.
Dies stimmt tatsächlich: Für $t \neq 0$ ist $x_1(t)$ konstant, also die Ableitung Null.
Bei $t=0$ ist die Steigung unendlich groß, was sich auch in der Gleichung $x_2(t) = 2 \cdot \delta(t)$ ausdrückt.
Das Impulsgewicht „2” der Diracfunktion berücksichtigt, dass der Sprung innerhalb der Funktion $x_1(t)$ bei $t = 0$ die Höhe $2$ hat.

Integrationssatz

Die Integration ist ebenso wie die Differentiation eine lineare Operation. Daraus ergibt sich der

$\text{Integrationssatz:}$ Ist $X(f)$ die Fouriertransformierte (Spektralfunktion) von $x(t)$ , so gelten auch die folgenden Fourierkorrespondenzen:

$\mathbf{(1)}\hspace{0.5cm}\int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )} \hspace{0.1cm}{\rm d}\tau \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ \ X( f )\left( {\frac{1}{{{\rm j}\cdot 2\pi f}} + \frac{1}{2}\cdot \delta ( f )} \right),$

$\mathbf{(2)}\hspace{0.5cm}x( t )\left( { - \frac{1}{{{\rm j}\cdot 2\pi t}} + \frac{1}{2}\cdot \delta ( t )} \right)\ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ \ \int_{ - \infty }^f {X( \nu ) \hspace{0.1cm}{\rm d}\nu .}$

$\text{Veranschaulichung – kein exakter Beweis:}$

Der Integrationssatz stellt genau die Umkehrung des Differentiationssatzes dar. Wendet man auf die obere Gleichung $\mathbf{(1)}$ den Differentiationssatz an, so erhält man:

$\frac{ {\rm d} }{ {\rm d}t} \int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )} \hspace{0.1cm}{\rm d}\tau\ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ \ X( f )\cdot \left( {\frac{1}{ { {\rm j}\cdot 2\pi f} } + \frac{1}{2}\cdot \delta ( f )} \right) \cdot {\rm j}\cdot 2\pi f.$

An diesem Beispiel zeigt sich die Gültigkeit des Integrationssatzes:

Die Differentiation nach der oberen Grenze auf der linken Seite liefert genau den Integranden $x(t)$ .
Auf der rechten Seite der Korrespondenz ergibt sich richtigerweise $X(f)$ , da die Diracfunktion bei $f=0$ wegen der Multiplikation mit $\text{j}\cdot 2\pi f$ ausgeblendet wird.

Hinweis: Alle in diesem Kapitel dargelegten Gesetzmäßigkeiten – unter Anderem auch der Differentiations– und der Integrationssatz – werden im Lernvideo Gesetzmäßigkeiten der Fouriertransformation an Beispielen verdeutlicht.

Zusammenhang Rechteck

$\ \leftrightarrow \$ Rampe

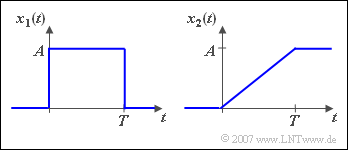
$\text{Beispiel 8:}$ Die skizzierten Signale $x_1(t)$ und $x_2(t)$ hängen wie folgt zusammen:

$x_2( t ) = \frac{1}{T}\cdot \int_{ - \infty }^{\hspace{0.05cm}t} {x_1 } ( \tau )\hspace{0.1cm}{\rm d}\tau .$

Aufgrund des Integrationssatzes gilt dann folgender Zusammenhang zwischen den Spektren:

$X_2 ( f ) = \frac{1}{T}\cdot X_1 ( f ) \cdot \left( {\frac{1}{{{\rm j}\cdot 2\pi f}} + \frac{1}{2}\cdot \delta ( f )} \right).$

Mit der Spektralfunktion

$X_1 ( f ) = A \cdot T \cdot {\rm si}( {\pi fT} ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}\pi fT}$

erhält man somit

$X_2 ( f ) = \frac{ {A } }{2}\cdot \delta ( f ) + \frac{ {A \cdot T} }{ {2{\rm j} } } \cdot \frac{ {\sin( {\pi fT}) } }{ {\left( {\pi fT} \right)^2 } } \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}\pi fT},$

bzw. nach trigonometrischen Umformungen:

$X_2 ( f ) = \frac{ {A} }{2}\cdot \delta ( f ) + \frac{ {A \cdot T} }{ { ( {2\pi fT} )^2 } }\cdot \big[ {\cos( {2\pi fT} ) - 1 - {\rm j}\cdot \sin ( {2\pi ft} )} \big].$

Hierzu ist anzumerken:

Die Diracfunktion bei $f = 0$ mit dem Gewicht $A/2$ berücksichtigt den Gleichanteil der Rampenfunktion $x_2(t)$ .
Das bedeutet auch: Der Gleichanteil der Rampenfunktion ist genau so groß wie der Gleichanteil der Sprungfunktion.
Das fehlende Dreieck mit den Eckpunkt–Koordinaten $(0, 0)$ , $(T, A)$ und $(0, A)$ ändert am Gleichanteil nichts.
Diese Dreieckfläche wirkt sich gegenüber der unendlich großen Restfläche (bis ins Unendliche gehend) nicht aus.