The Fourier Transform Theorems

Multiplication With a Factor - Addition Theorem

In this section the Fourier Transform Theorems are assembled. These can be used to e.g. derive from already known transformations

$x( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X( f ),\quad x_1 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_1 ( f ),\quad x_2 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_2 ( f )$

new functional relationships. Here we restrict ourselves to real time functions.

$\text{Theorem:}$ A constant factor $k$ affects the time and spectral function in the same way:

$k \cdot x(t)\ \;\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ k \cdot X(f).$

This relation can be used for simplification by omitting the constant $k$ (which can be a gain-, a damping- or a unit-factor) and adding it to the result later.

The above sentence follows directly from the definition of the first Fourier integral, as well as from the addition theorem, which formulates the foundation of the superposition principle .

$\text{Addition Theorem:}$ If a time function can be written as a sum of single functions, the resulting spectral function is the sum of the resulting single spectra:

$x( t ) = x_1 ( t ) + x_2 ( t )\quad\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad X( f ) = X_1 (f) + X_2 ( f ).$

Rectangular pulse, triangular pulse and their combination

$\text{Example 1:}$ The following Fourier correspondences are known:

The rectangular pulse:

$x_1 ( t )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X_1 ( f )=T \cdot {\rm si}(\pi f T),$

The triangle pulse:

$x_2 ( t )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X_2 ( f )=T /2\cdot {\rm si}(\pi f T/2).$

These two impulse signals are sketched as red and blue curve respectively.

Then the green drawn (weighted) sum signal is valid:

$x(t) = {1}/{3} \cdot x_1 ( t ) + {2}/{3} \cdot x_2 ( t )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X(f) = {1}/{3} \cdot X_1 ( f ) + {2}/{3} \cdot X_2 ( f ).$

Notes: All theorems presented in this chapter can be found at the german learning video Fourier Transform Laws with illustrated examples.

Mapping Theorem

With the Complex Fourier Series for describing periodic signals, we have found out that that an even function always leads to real Fourier coefficients and an odd function exclusively to imaginary Fourier coefficients. The Fourier transform shows similar properties.

$\text{Mapping Theorem:}$ If a real time function consists additively of an even and an uneven part,

$x( t ) = x_{\rm g} ( t ) + x_{\rm u} ( t ),$

then the following applies for its spectral function:

$X(f) = X_{\rm R}(f) + {\rm j}\cdot X_{\rm I}(f), \hspace{0.5cm}\text{with}$

$x_{\rm g} (t) \hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X_{\rm R}(f),$

$x_{\rm u} (t) \hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} {\rm j} \cdot X_{\rm I} (f).$

The real part $X_{\rm R}(f)$ of the spectrum is then also even, while $X_{\rm I}(f)$ describes an odd function of the frequency.

The assignment theorem can be easily proved by considering the theorem of Leonhard Euler ⇒ ${\rm e}^{ - {\rm j}\omega _0 t} = \cos ( {\omega _0 t} ) - {\rm j}\cdot \sin ( {\omega _0 t} )$ . The even and odd part of a function $x(t)$ can be calculated with the following equations:

$x_{\rm g} (t) = {1}/{2}\big[ {x(t) + x(-t)} \big],$

$x_{\rm u} (t) = {1}/{2}\big[ {x(t) - x(-t)} \big].$

Spectrum of a Jumping Function

$\text{Example 2:}$ We consider the Jump Function

$x(t) = \gamma (t) = \bigg\{ \begin{array}{l} 0\quad \quad {\rm f\ddot{u} r}\;t < 0 \\ 1\quad \quad{\rm f\ddot{u} r}\; t > 0 \\ \end{array} ,$

which can be split as follows:

$\gamma (t) = {1}/{2} +{1}/{2} \cdot {\rm sign}(t).$

The Signum function was used here:

${\rm sign} (t) = \bigg\{ \begin{array}{l} -1\quad \quad {\rm f\ddot{u} r}\;t < 0, \\ +1\quad \quad{\rm f\ddot{u} r}\; t > 0. \\ \end{array}$

Therefore the following applies:

The even (blue) signal portion $x_{\rm g} (t) = {1}/{2}$ is a constant with the real spectral function $X_{\rm R}(f) = {1}/{2} \cdot \delta(f)$ .
The spectrum ${\rm j} \cdot X_{\rm I}(f)$ the odd (green) signum function $x_{\rm u} (t)$ was already calculated in the earlier $\text{Example 3}$ n the page „Fouriertransformation”.
This results in the jump function&nbsp for the resulting spectrum of the red sketched jump function;

$X(f) = X_{\rm R}(f) + {\rm j}\cdot X_{\rm I}(f)= {1}/{2} \cdot \delta (f) - {\rm j}\cdot \frac{1}{2\pi f}.$

Similarity Theorem

The similarity theorem shows the relation between the spectral functions of two time signals of the same shape, stretched or compressed.

$\text{Simity Theoremlari:}$ If $X(f)$ the Fourier transform of $x(t)$ , then with the real constant $k$ the following relation appliesg:

$x( {k \cdot t} )\hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} \frac{1}{\left \vert k \right \vert} \cdot X( {f}/{k} ).$

$\text{Proof:}$ For positive $k$ follows from the Fourier integral with the substitution $\tau = k \cdot t$ :

$\int_{ - \infty }^{ + \infty } {x( {k \cdot t})} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}ft} \hspace{0.1cm}{\rm d}t = \frac{1}{k} \cdot \int_{ - \infty }^{ + \infty } {x( \tau )} \cdot {\rm e}^{ - {\rm j}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm} f/k \hspace{0.05cm}\cdot \hspace{0.05cm}\tau } \hspace{0.1cm}{\rm d} \tau = \frac{1}{k}\cdot X( {{f}/{k}}).$

For negative $k$ the integration limits would be mixed up and you get $-1/k \cdot X(f/k)$ .
Since in the equation $\vert k \vert$ is used, the result is valid for both signs.

q.e.d.

The effects of the similarity theorem can be illustrated with a tape for example. If such a tape is played with double speed, this corresponds to a compression of the time signal $(k = 2)$ . Thus the frequencies appear twice as high.

Two Rectangles of different width

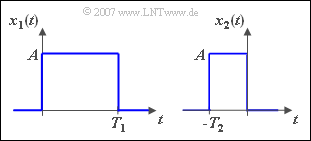
$\text{Example 3:}$ Wir betrachten zwei Rechtecke gleicher Höhe, wobei $T_2 = T_1/2$ gilt.

The spectral function of $x_1(t)$ results after the first Fourier Integral to

$X_1 (f) = A \cdot \frac{ {1 - {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } } }{ { {\rm j}2\pi f} } .$

For this can also be written:

$X_1 (f) = A \cdot T_1 \cdot \frac{{{\rm e}^{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } - {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } }}{{{\rm j}2\pi fT_1 }} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 } = A \cdot T_1 \cdot {\rm si}( {\pi f T_1 } ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_1 }.$

For the spectral function of $x_2(t)$ follows from the similarity theorem with $k = -2$ :

$X_2 (f) = \frac{1}{2} \cdot X_1 ( { - {f}/{2}} ) = \frac{A \cdot T_1 }{2} \cdot {\rm si}( { - \pi f {T_1 }/{2} } ) \cdot {\rm e}^{ {\rm j}\pi fT_1 /2} .$

The $\text{si}$ –function is even: $\text{si}(-x) = \text{si}(x)$ . Therefore you can omit the sign in the argument of the $\text{si}$ –function.

With $T_2 = T_1/2$ one gets:

$X_2 (f) = A \cdot T_2 \cdot {\rm si}( {\pi fT_2 } ) \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}fT_2 } .$

Reciprocity Theorem of Time duration and Bandwidth

This law follows directly from the Signal_Representation/Fourier_Transform_Laws#.C3.84hnlichkeitssatz|Similarity Theorem]]: The wider an impulse is in its extension, the narrower and higher is the corresponding spectrum and vice versa.

To be able to make quantitative statements, we define two parameters for energy-limited signals ⇒ Impulse. Both quantities are shown in the diagram for the $\text{Example 4}$ for a Gaussian pulse and its likewise Gaussian spectrum.

$\text{Definition:}$ The equivalent pulse duration is derived from the time course. It is equal to the width of an area equal rectangle with the same height as $x(t)$ :

$\Delta t = \frac{1}{{x( {t = 0} )}} \cdot \int_{ - \infty }^{ + \infty } {x( t)} \hspace{0.1cm}{\rm d}t.$

$\text{Definition:}$ The equivalent bandwidth denotes the impulse in the frequency domain. It gives the width of the area equal rectangle with the same height as the spectrum $X(f)$ :

$\Delta f = \frac{1}{{X( {f = 0} )}}\cdot \int_{ - \infty }^{ + \infty } {X( f )} \hspace{0.1cm} {\rm d}f.$

$\text{Reciprocity Theorem:}$ Das Produkt aus äquivalenter Impulsdauer und äquivalenter Bandbreite ist stets gleich $1$ :

$\Delta t \cdot \Delta f = 1$

$\text{Proof:}$ Based on the two Fourier integrals, for $f = 0$ or. $t = 0$ :

$X( {f = 0} ) = \int_{ - \infty }^{ + \infty } {x(t)\hspace{0.1cm}{\rm d}t,} \hspace{0.5cm}x( {t = 0} ) = \int_{ - \infty }^{ + \infty } {X(f)\hspace{0.1cm}{\rm d}f.}$

If you take this result into account in the above definitions, you get

$\Delta t = \frac{{X( {f = 0} )}}{{x( {t = 0} )}}, \hspace{0.5cm}\Delta f = \frac{{x( {t = 0} )}}{{X( {f = 0} )}}.$

From this

$\Delta t \cdot \Delta f = 1$ follows directly.

q.e.d.

Note that $\Delta f$ is defined over the actual spectrum $X(f)$ and not over $|X(f)|$ .

For real functions the integration over the even function part is sufficient, since the integral over the odd part is always zero due to the Mapping Theorem .
For odd time functions and thus purely imaginary spectra, the two definitions of $\Delta t$ and. $\Delta f$ fail.

Gauß–Beispiel zum Reziprozitätsgesetz

$\text{Example 4:}$ The graph illustrates the equivalent pulse duration $\Delta t$ and the equivalent bandwidth $\Delta f$ exemplary for the Gaussian pulse Furthermore , it is valid:

Widening the Gaussian pulse by the factor $3$ will reduce the equivalent bandwidth by the same factor.
If the pulse amplitude $x(t = 0)$ is not changed, the integral area above $X(f)$ remains constant.
This means that $X(f=0)$ is simultaneously increased by the factor $3$ .

Vertauschungssatz

Diese Gesetzmäßigkeit ist besonders nützlich, um neue Fourierkorrespondenzen zu erhalten.

$\text{Vertauschungssatz:}$ If $X(f)$ is the Fourier Transform of $x(t)$ , then:

$X^{\star}(t)\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}x^{\star}( f ).$

If we restrict ourselves to real time functions, the signs for "conjugated complex" can be omitted on both sides of the Fourier correspondence.

$\text{Proof:}$ The first Fourier Integral is after successive renaming $t \to u$ ,respectively $f \to t$ :

$X( f ) = \int_{ - \infty }^{ + \infty } {x( u )} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}u} \hspace{0.1cm}{\rm d}u, \hspace{1cm} X(t ) = \int_{ - \infty }^{ + \infty } {x( u )} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}t\hspace{0.05cm}\cdot \hspace{0.05cm}u}\hspace{0.1cm} {\rm d}u.$

If you change the sign in the exponent, you have to replace $X(t)$ by $X^*(t)$ and $x(u)$ by $x^*(u)$ :

$X^{\star}(t ) = \int_{ - \infty }^{ + \infty } {x^{\star}( u )} \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi\hspace{0.05cm}\cdot \hspace{0.05cm} t\hspace{0.05cm}\cdot \hspace{0.05cm}u}\hspace{0.1cm} {\rm d}u.$

With the further renaming $u \to f$ one gets to the second Fourier Integral:

$X^{\star}(t ) = \int_{ - \infty }^{ + \infty } {x^{\star}( f )} \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}f.\hspace{7.9cm}$

q.e.d.

Rectangle

$\ \leftrightarrow \ \ \rm si$ –Pulse

$\text{Example 5:}$ The spectrum $X(f) = \delta(f)$ of the DC signal $x(t) = 1$ is assumed to be known.

According to the permutation theorem, the spectral function of the Dirac impulse is therefore $x(t) = \delta(t)$ :

$x(t) = \delta(t)\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm} X(f)= 1.$

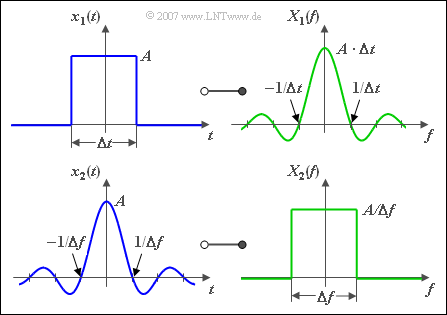
The figure shows another application of the swapping theorem, namely the functional relations between

a signal $x_1(t)$ with rectangular time function, and
a signal $x_2(t)$ with rectangular spectral function.

Shifting Theorem

We now consider a shift of the time function - for example caused by a running time - or a frequency shift, as it occurs for example with (analog) Zweiseitenband–Amplitude Modulation .

$\text{Shifting Theorem:}$ If $X(f)$ is the Fourier Transform of $x(t)$ , the following correlations also apply:

$\mathbf{(1)}\hspace{0.5cm}x( {t - t_0 } )\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X( f ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm} f\hspace{0.05cm}\cdot \hspace{0.05cm}t_0 },$

$\mathbf{(2)}\hspace{0.5cm}x( t ) \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f_0 \hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}X( {f - f_0 } ).$

Here $t_0$ and $f_0$ are any time or frequency values.

$\text{Proof of Equation (1):}$ The first Fourier Integral for the signal $x_{\rm V}(t) = x(t-t_0)$ shifted to the right by $t_0$ is defined as following with the substitution $\tau = t - t_0$ :

$X_{\rm V} ( f ) = \int_{ - \infty }^{ + \infty } {x( {t - t_0 } ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm}{\rm d}t} = \int_{ - \infty }^{ + \infty } {x( \tau ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}( {\tau + t_0 } )}\hspace{0.1cm} {\rm d}\tau .}$

The term independent from the integration variable $\tau$ can be dragged in front of the integral. With the renaming $\tau \to t$ one then obtains

$X_{\rm V}( f ) = {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t_0 } \cdot \int_{ - \infty }^{ + \infty } {x( t )} \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}t = {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t_0 } \cdot X( f).$

q.e.d.

Beispiel zum Verschiebungssatz

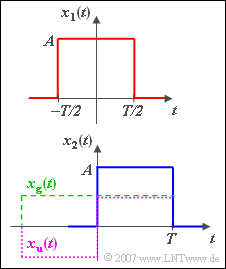
$\text{Example 6:}$ As already mentioned, the symmetrical rectangular pulse $x_1(t)$ has the following spectrum

$X_1 ( f ) = A \cdot T \cdot {\rm si}( {\pi fT} ).$

The rectangular pulse $x_2(t)$ displayed below is shifted to the right with respect to $x_1(t)$ by $T/2$ :

$x_2(t) = x_1(t-T/2).$

Thus its spectrum is:

$X_2( f ) = A \cdot T \cdot {\rm si}( {\pi fT} ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}T} .$

This spectral function can also be written as follows with the Theorem of Euler and some simple trigonometric transformations:

$X_2( f ) = \frac{A }{2\pi f} \cdot \sin ( 2\pi fT) + {\rm j}\cdot \frac{A }{2\pi f} \cdot \big[ {\cos ( {2\pi fT} ) - 1} \big] .$

The same result can be obtained with the Mapping Theorem:

The real part of the spectrum belongs to the even signal part $x_{\rm g}(t)$ , the imaginary part to the odd part $x_{\rm u}(t)$ .

Differentiation Theorem

This theorem shows, how the differentiation of a function $x(t)$ resp. $X(f)$ affects the corresponding Fourier-transform; it is also applicable several times.

A simple example for the application of the differentiation theorem is the relation between the current $i(t)$ and the voltage $u(t)$ a capacitance $C$ according to the equation $i(t) = C \cdot \text{d}u(t)/\text{d}t$ .

$\text{Differentiation Theorem:}$ If $X(f)$ is the Fourier transform of $x(t)$ , the following two correspondences are also valid:

$\mathbf{(1)}\hspace{0.5cm}\frac{{{\rm d}x( t )}}{{{\rm d}t}}\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi f \cdot X( f ),$

$\mathbf{(2)}\hspace{0.5cm}- t \cdot x( t )\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\hspace{0.15cm}\frac{1}{{{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi }} \cdot \frac{{{\rm d}X( f )}}{{{\rm d}f}}.$

$\text{Proof of Equation (1):}$ The first equation results from differentiation of the second Fourier Integral:

$y(t) = \frac{\text{d}x(t)}{\text{d}t} = \frac{\text{d} }{\text{d}t}\int_{ - \infty }^{ + \infty } X( f ) \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\hspace{0.03cm}\pi\hspace{0.05cm}\cdot \hspace{0.05cm} f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}f = \int_{ - \infty }^{ + \infty } {X( f )} \cdot {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi f \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\pi \hspace{0.05cm}\cdot \hspace{0.05cm} f\hspace{0.05cm}\cdot \hspace{0.05cm}t} {\rm d}f.$

At the same time:

$y( t ) = \int_{ - \infty }^{ + \infty } {Y( f )} \cdot {\rm e}^{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}2\hspace{0.03cm}\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}f.$

By comparing the integrands, the variation $\mathbf{(1)}$ of the differentiation theorem is obtained.
To derive the second variant one proceeds from the

first Fourier Integral in an analogous manner.

The negative exponent in the first Fourier integral leads to the minus sign in the time function.
q.e.d.

Correlation Jump

$\ \leftrightarrow \$ Dirac

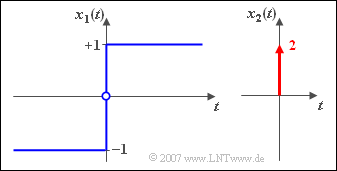
$\text{Example 7:}$ The spectra of the signals $x_1(t)$ and $x_2(t)$ were already calculated in the previous examples as following:

$X_1( f ) = \frac{1 }{ {\rm j\cdot \pi} f}, \hspace{1cm} X_2( f ) = 2 = {\rm const.}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} X_2(f) = X_1(f) \cdot {\rm j}\cdot 2\pi f.$

From the differentiation theorem it follows that $x_2(t)$ is equal to the time-derivative of $x_1(t)$ .
This is actually correct: For $t \neq 0$ is $x_1(t)$ constant, i.e. the derivative is zero.
For $t=0$ the gradient is infinitely large, which is also expressed in the equation $x_2(t) = 2 \cdot \delta(t)$
The impulse weight "2" of the Dirac function considers that the jump within the function $x_1(t)$ at $t = 0$ has the height $2$

Integration Theorem

Integration is a linear operation just like differentiation. This results in the

$\text{Integration Theorem:}$ If $X(f)$ is the Fourier Transform (spectral function) of $x(t)$ , then the following Fourier correspondences also apply:

$\mathbf{(1)}\hspace{0.5cm}\int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )} \hspace{0.1cm}{\rm d}\tau \ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ \ X( f )\left( {\frac{1}{{{\rm j}\cdot 2\pi f}} + \frac{1}{2}\cdot \delta ( f )} \right),$

$\mathbf{(2)}\hspace{0.5cm}x( t )\left( { - \frac{1}{{{\rm j}\cdot 2\pi t}} + \frac{1}{2}\cdot \delta ( t )} \right)\ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \ \ \int_{ - \infty }^f {X( \nu ) \hspace{0.1cm}{\rm d}\nu .}$

$\text{Illustration – no exact proof:}$

The integration theorem represents exactly the inversion of the differentiation theorem . . If one applies the differentiation theorem to the upper equation $\mathbf{(1)}$ one obtains

$\frac{ {\rm d} }{ {\rm d}t} \int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )} \hspace{0.1cm}{\rm d}\tau\ \ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ \ X( f )\cdot \left( {\frac{1}{ { {\rm j}\cdot 2\pi f} } + \frac{1}{2}\cdot \delta ( f )} \right) \cdot {\rm j}\cdot 2\pi f.$

This example shows the validity of the integration theorem:

The differentiation according to the upper limit on the left side yields exactly the integrand $x(t)$ .
On the right side of the correspondence correctly results in $X(f)$ , since the Dirac function is hidden with $f=0$ because of the multiplication with $\text{j}\cdot 2\pi f$ .

Notes: All theorems shown in this page – such as the integration and differentiation theorem – will be elucidated with examples in the german learning video Gesetzmäßigkeiten der Fouriertransformation .

Correlation of Rectangle

$\ \leftrightarrow \$ Ramp

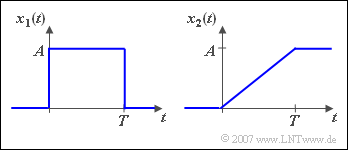
$\text{Example 8:}$ The sketched signals $x_1(t)$ and $x_2(t)$ are related as follows

$x_2( t ) = \frac{1}{T}\cdot \int_{ - \infty }^{\hspace{0.05cm}t} {x_1 } ( \tau )\hspace{0.1cm}{\rm d}\tau .$

Due to the integration theorem the following relation between the spectra applies:

$X_2 ( f ) = \frac{1}{T}\cdot X_1 ( f ) \cdot \left( {\frac{1}{{{\rm j}\cdot 2\pi f}} + \frac{1}{2}\cdot \delta ( f )} \right).$

With the spectral function

$X_1 ( f ) = A \cdot T \cdot {\rm si}( {\pi fT} ) \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}\pi fT}$

one gets

$X_2 ( f ) = \frac{ {A } }{2}\cdot \delta ( f ) + \frac{ {A \cdot T} }{ {2{\rm j} } } \cdot \frac{ {\sin( {\pi fT}) } }{ {\left( {\pi fT} \right)^2 } } \cdot {\rm e}^{ - {\rm j}\hspace{0.05cm}\cdot\hspace{0.05cm}\pi fT},$

or after trigonometric transformations:

$X_2 ( f ) = \frac{ {A} }{2}\cdot \delta ( f ) + \frac{ {A \cdot T} }{ { ( {2\pi fT} )^2 } }\cdot \big[ {\cos( {2\pi fT} ) - 1 - {\rm j}\cdot \sin ( {2\pi ft} )} \big].$

It should be noted here:

The Dirac function at $f = 0$ with the weight $A/2$ considers the DC component of the ramp function $x_2(t)$ .
This also means: the DC component of the ramp function is exactly the same as the DC component of the jump function.
The missing triangle with the corner point coordinates $(0, 0)$ , $(T, A)$ and $(0, A)$ does not change the DC component.
This triangular area has no effect compared to the infinite remaining area (going to infinity).