Some Preliminary Remarks on Two-Dimensional Random Variables

1 # OVERVIEW OF THE THIRD MAIN CHAPTER #
2 Introductory example on the statistical dependence of random variables
3 Prerequisites and nomenclature
4 Wahrscheinlichkeitsfunktion und Wahrscheinlichkeitsdichtefunktion
5 Wahrscheinlichkeitsfunktion und Entropie
6 Relative Entropie – Kullback–Leibler–Distanz
7 Verbundwahrscheinlichkeit und Verbundentropie
8 Aufgaben zum Kapitel
9 Quellenverzeichnis

# OVERVIEW OF THE THIRD MAIN CHAPTER #

The focus of this third main chapter is the mutual information $I(X; Y)$ between two random variables $X$ and $Y$. With statistical dependence, $I(X; Y)$ is smaller than the individual entropies $H(X)$ or $H(Y)$. For example, the uncertainty regarding the random variable $X$ ⇒ entropy $H(X)$ is reduced by the knowledge of $Y$ , by the amount $H(X\hspace{0.03cm}|\hspace{0.03cm}Y)$ ⇒ conditional entropy of $X$, falls $Y$ is known. The remaining residue is the mutual information $I(X; Y)$. At the same time, however $I(X; Y) = H(Y) - H(Y\hspace{0.03cm}|\hspace{0.03cm}X)$. The semicolon indicates that the two random variables under consideration, $X$ and $Y$ , are equal.

In detail, the third main chapter deals with:

the relationship between probability and entropy for 2D random variables,
the calculation of the relative entropy, , also known as the Kullback–Leibler distance ,
the definition of the joint entropie $H(XY)$ and the conditional entropies $H(X\hspace{0.03cm}|\hspace{0.03cm}Y)$ and $H(Y\hspace{0.03cm}|\hspace{0.03cm}X)$,
the mutual information $I(X; Y)$ between two random variables ,
the information theory of digital signal transmission and the corresponding model,
the definition and meaning of the channel capacity and its connection with the mutual information,
the capacity calculation for digital memoryless channels such as BSC, BEC and BSEC,
the channel coding theorem, one of the highlights of Shannon's information theory.

Further information on the topic as well as tasks, simulations and programming exercises can be found in the experiment „Wertdiskrete Informationstheorie” of the practical course „Simulation Digitaler Übertragungssysteme ”. This (former) LNT course at the TU Munich is based on

the windows programme WDIT ⇒ link refers to the ZIP version of the programme; and
the corresponding Praktikumsanleitung ⇒ link refers to the PDF version.

Introductory example on the statistical dependence of random variables

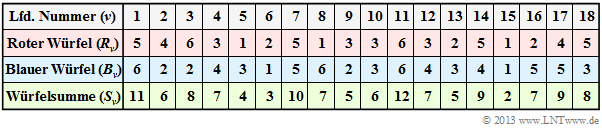
$\text{Example 1:}$ We start from the experiment „rolling two dice” aus, where both dice are distinguishable (by colour). The table shows the results of the first $N = 18$ pairs of throws of this exemplary random experiment.

Result protocol of our random experiment „throwing two dice”

Note: According to the nomenclature explained in the following section r $R_ν$, $B_ν$ and $S_ν$ are to be understood as random variables here:

For example, the random variable $R_3 \in \{1, \ 2, \ 3, \ 4, \ 5, \ 6\}$ indicates the number of eyes of the red die on the third throw as a probability event. The specification $R_3 = 6$ states that in the documented realisation the red die showed a „6” in the third throw.

In line 2, the numbers of the red dice $(R)$ are indicated. The mean value of this limited sequence $〈R_1$, ... , $R_{18}〉$ is with $3.39$ smaller than the expected value ${\rm E}\big[R\big] = 3.5$. Line 3 shows the numbers of eyes of the blue cube $(B)$. The sequence $〈B_1$, ... , $B_{18}〉$ has a slightly larger mean value of $3.61$ einen has a slightly larger mean value of ⇒ ${\rm E}\big[B\big] = 3.5$.
Line 4 contains the sum $S_ν = R_ν + B_ν$. The mean value of the sequence $〈S_1$, ... , $S_{18}〉$ is $3.39 + 3.61 = 7$. This is here (by chance) equal to the expected value $\text{E}\big[S\big] = \text{E}\big[R\big] + \text{E}\big[B\big]$.

Now the question arises between which random variables there are statistical dependencies:

If one assumes fair dice, there are no statistical ties between the sequences $〈 R\hspace{0.05cm} 〉$ and $〈B \hspace{0.05cm}〉$ – whether bounded or unbounded: Even if one knows $R_ν$ for $B_ν$ all possible numbers of eyes $1$, ... , $6$ are equally probable.
If one knows $S_ν$, however, statements about $R_ν$ as well as about $B_ν$ are possible. From $S_{11} = 12$ follows directly $R_{11} = B_{11} = 6$ and the sum $S_{15} = 2$ of two dice is only possible with two ones. Such dependencies are called deterministic.
From $S_7 = 10$ , at least ranges for $R_7$ and $B_7$ can be given: $R_7 ≥ 4, \ B_7 ≥ 4$. Then only the three pairs of values $(R_7 = 4) ∩ (B_7 = 6)$, $(R_7 = 5) ∩ (B_7 = 5)$ as well as $(R_7 = 6) ∩ (B_7 = 4)$ are possible. Here there is no deterministic relationship between the random variables $S_ν$ and $R_ν$ $($or. $B_ν)$, but rather a so-called statistical dependence.
Such statistical dependencies exist for $S_ν ∈ \{3, \ 4, \ 5, \ 6, \ 8, \ 9, \ 10, \ 11\}$. If, on the other hand, the sum $S_ν = 7$, one cannot infer $R_ν$ and $B_ν$ from this. For both dice, all possible numbers $1$, ... , $6$ are equally probable. In this case, there are also no statistical ties between $S_ν$ and $R_ν$ or between $S_ν$ and $B_ν$.

Prerequisites and nomenclature

Throughout this chapter, we consider discrete-value random variables of the form $X = \{ x_1, \ x_2, \hspace{0.05cm}$ ... $\hspace{0.05cm},\ x_{\mu},\hspace{0.05cm}$ ... $\hspace{0.05cm},\ x_M \} \hspace{0.05cm},$ , and use the following nomenclature:

The random variable itself is always denoted by a capital letter. The lower case letter $x$ indicates a possible realisation of the random variable $X$ .
All realisations $x_μ$ $($with $μ = 1$, ... , $M)$ are real-valued. $M$ indicates the symbol set size of of $X$ . Instead of $M$ , we sometimes also use $|X|$.

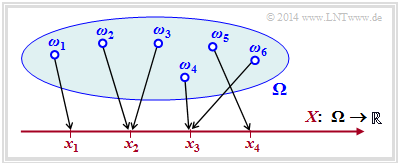
Relationship between the probability space ${\it \Omega}$
and the random variable $X$

The random variable $X$ can, for example, be created by the transformation $\Omega → X$ , where $\Omega$ stands for the probability space of a random experiment.

The diagram illustrates such a transformation:

$${\it \Omega} = \{ \omega_1, \omega_2, \omega_3, ... \hspace{0.15cm} \} \hspace{0.25cm} \longmapsto \hspace{0.25cm} X = \{ x_1, \ x_2, \ x_3, \ x_4\} \subset \cal{R}\hspace{0.05cm}.$$

Each random event $ω_i ∈ Ω$ is uniquely assigned to a real numerical value $x_μ ∈ X ⊂ ℝ$ .
In the example considered, the running variable is $1 ≤ μ ≤ 4$, , i.e. the symbol range is $M = |X| = 4$.
However, the figure is not one-to-one: the realisation $x_3 ∈ X$ could have resulted from the elementary event $ω_4$ in the example, but also from $ω_6$ $($or from some other of the infinitely many elementary events $ω_i not drawn in the diagram)$.

$\text{Agreement:}$ Often one refrains from indexing both the elementary events $ω_i$ and the realisations $x_μ$. This results in the following shorthand notations, for example:

$$ \{ X = x \} \hspace{0.05cm} \equiv \hspace{0.05cm} \{ \omega \in {\it \Omega} : \hspace{0.4cm} X(\omega) = x \} \hspace{0.05cm},$$

$$ \{ X \le x \} \hspace{0.05cm} \equiv \hspace{0.05cm} \{ \omega \in {\it \Omega} : \hspace{0.4cm} X(\omega) \le x \} \hspace{0.05cm}.$$

With this agreement, the probabilities of the discrete random variable $X$ are:

$${\rm Pr}( X = x_{\mu}) = \hspace{-0.2cm} \sum_{\omega \hspace{0.1cm} \in \{ X = x_{\mu} \} } \hspace{-0.2cm}{\rm Pr} \left ( \{ \omega \} \right ) \hspace{0.05cm}.$$

Wahrscheinlichkeitsfunktion und Wahrscheinlichkeitsdichtefunktion

$\text{Definition:}$ Fasst man die $M$ Wahrscheinlichkeiten einer diskreten Zufallsgröße $X$ ⇒ ${\rm Pr}( X = x_{\mu})$ ähnlich wie bei einem Vektor zusammen, so kommt man zur Wahrscheinlichkeitsfunktion (englisch: Probability Mass Function, PMF):

$$P_X(X) = \big [ \hspace{0.02cm} P_X(x_1), P_X(x_2), \hspace{0.05cm}\text{...} \hspace{0.15cm}, P_X(x_{\mu}),\hspace{0.05cm} \text{...}\hspace{0.15cm}, P_X(x_M) \hspace{0.02cm} \big ] \hspace{0.05cm}.$$

Das $μ$–te Element dieses „Vektors” gibt dabei die Wahrscheinlichkeit $P_X(x_{\mu}) = {\rm Pr}( X = x_{\mu}) $ an.

Im Buch„Stochastische Signaltheorie” haben wir mit der Wahrscheinlichkeitsdichtefunktion $($WDF, englisch: Probability Density Function, PDF$)$ eine ähnliche Beschreibungsgröße definiert und diese mit $f_X(x)$ bezeichnet.

Zu beachten ist aber:

Die PDF eignet sich eher zur Charakterisierung kontinuierlicher Zufallsgrößen, wie zum Beispiel bei einer Gaußverteilung oder einer Gleichverteilung. Erst durch die Verwendung von Diracfunktionen wird die PDF auch für diskrete Zufallsgrößen anwendbar.
Die PMF liefert weniger Information über die Zufallsgröße als die PDF und kann zudem nur für diskrete Größen angegeben werden. Für die in diesem Kapitel betrachtete wertdiskrete Informationstheorie ist die PMF allerdings ausreichend.

$\text{Beispiel 2:}$ Wir betrachten eine Wahrscheinlichkeitsdichtefunktion (abgekürzt WDF bzw. PDF) ohne großen Praxisbezug:

$$f_X(x) = 0.2 \cdot \delta(x+2) + 0.3 \cdot \delta(x - 1.5)+0.5 \cdot \delta(x - {\rm \pi}) \hspace{0.05cm}. $$

Für die diskrete Zufallsgröße gilt somit $x ∈ X = \{–2,\ +1.5,\ +\pi \} $ ⇒ Symbolumfang $M = \vert X \vert = 3$, und die Wahrscheinlichkeitsfunktion (PMF) lautet:

$$P_X(X) = \big [ \hspace{0.1cm}0.2\hspace{0.05cm}, 0.3\hspace{0.05cm}, 0.5 \hspace{0.1cm} \big] \hspace{0.05cm}. $$

Man erkennt:

Die PMF liefert nur Informationen über die Wahrscheinlichkeiten $\text{Pr}(x_1)$, $\text{Pr}(x_2)$ und $\text{Pr}(x_3)$.
Aus der PDF sind dagegen auch die möglichen Realisierungen $x_1$, $x_2$ und $x_3$ der Zufallsgröße $X$ ablesbar.
Die einzige Voraussetzung für die Zufallsgröße ist, dass sie reellwertig ist.
Die möglichen Werte $x_μ$ müssen weder positiv, ganzzahlig, äquidistant noch rational sein.

Wahrscheinlichkeitsfunktion und Entropie

In der wertdiskreten Informationstheorie genügt im Gegensatz zu übertragungstechnischen Problemen schon die Kenntnis der Wahrscheinlichkeitsfunktion $P_X(X)$, zum Beispiel zur Berechnung der Entropie.

$\text{Definition:}$ Die Entropie einer diskreten Zufallsgröße $X$ – also deren Unsicherheit für einen Beobachter – kann man mit der Wahrscheinlichkeitsfunktion $P_X(X)$ wie folgt darstellen:

$$H(X) = {\rm E} \big [ {\rm log} \hspace{0.1cm} \frac{1}{P_X(X)}\big ] \hspace{0.05cm}=\hspace{0.05cm} - {\rm E} \big [ {\rm log} \hspace{0.1cm} {P_X(X)}\big ] \hspace{0.05cm}=\hspace{0.05cm} \sum_{\mu = 1}^{M} P_X(x_{\mu}) \cdot {\rm log} \hspace{0.1cm} \frac{1}{P_X(x_{\mu})} \hspace{0.05cm}=\hspace{0.05cm} - \sum_{\mu = 1}^{M} P_X(x_{\mu}) \cdot {\rm log} \hspace{0.1cm} {P_X(x_{\mu})} \hspace{0.05cm}.$$

Verwendet man den Logarithmus zur Basis $2$, also $\log_2$ (...) ⇒ Logarithmus dualis, so wird der Zahlenwert mit der Pseudo–Einheit „bit” versehen. $\rm E\big[$...$\big]$ gibt den Erwartungswert an.

Beispielsweise erhält man

für $P_X(X) = \big [\hspace{0.02cm}0.2, \ 0.3, \ 0.5 \hspace{0.02cm}\big ]$:

$$H(X) = 0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} + 0.3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.3} +0.5 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.5} \approx 1.485\,{\rm bit}\hspace{0.05cm},$$

für $P_X(X) = \big [\hspace{0.02cm}1/3, \ 1/3, \ 1/3\hspace{0.02cm}\big ]$:

$$H(X) = 3 \cdot 1/3 \cdot {\rm log}_2 \hspace{0.1cm} (3) = {\rm log}_2 \hspace{0.1cm} (3) \approx 1.585\,{\rm bit}\hspace{0.05cm}.$$

Das zweite Beispiel liefert das Maximum der Entropiefunktion für den Symbolumfang $M = 3$.

$\text{Herleitung:}$ Für ein allgemeines $M$ lässt sich dieses Ergebnis beispielsweise wie folgt herleiten – siehe [Meck]^[1]:

$$H(X) = -{\rm E} \big [ {\rm log} \hspace{0.1cm} {P_X(X)}\big ] \hspace{0.2cm} \le \hspace{0.2cm}- {\rm log} \big [ {\rm E} \hspace{0.1cm} \left [{P_X(X)}\right ] \big ] \hspace{0.05cm}.$$

Diese Abschätzung $($Jensens's Ungleichung$)$ ist zulässig, da der Logarithmus eine konkave Funktion ist. Entsprechend der Aufgabe 3.2 gilt:

$$- {\rm E} \big [ {P_X(X)}\big ] \hspace{0.1cm} \le \hspace{0.1cm} M \hspace{0.3cm} \Rightarrow \hspace{0.3cm} H(X) \le {\rm log} \hspace{0.1cm} (M) \hspace{0.05cm}.$$

Das Gleichheitszeichen ergibt sich nach der oberen Rechnung für gleiche Wahrscheinlichkeiten, also für $P_X(x_μ) = {1}/{M}$ für alle $μ$. In der Aufgabe 3.3 soll der gleiche Sachverhalt unter Verwendung der Abschätzung

$${\rm ln} \hspace{0.1cm} (x) \le x-1$$

nachgewiesen werden. Das Gleichheitszeichen gilt hier nur für $x = 1$.

Ist eine der $M$ Wahrscheinlichkeiten $P_X(x_μ)$ der Wahrscheinlichkeitsfunktion gleich Null, so lässt sich für die Entropie eine engere Schranke angeben:

$$H(X) \le {\rm log} \hspace{0.1cm} (M-1) \hspace{0.05cm}.$$

$\text{Vereinbarung:}$ Im folgenden Beispiel und auf den nächsten Seiten verwenden wir die folgende Nomenklatur:

Die Entropie $H(X)$ bezieht sich stets auf die tatsächliche Wahrscheinlichkeitsfunktion $P_X(X)$ der diskreten Zufallsgröße. Experimentell erhält man diese Größen erst nach $N → ∞$ Versuchen.
Ermittelt man die Wahrscheinlichkeitsfunktion aus einer endlichen Zufallsfolge, so bezeichnen wir diese Wahrscheinlichkeitsfunktion mit $Q_X(X)$ und die daraus resultierende Entropie versehen wir mit dem Zusatz „$N =$ ...”.
Diese Entropie–Näherung basiert nicht auf Wahrscheinlichkeiten, sondern nur auf den relativen Häufigkeiten. Erst für $N → ∞$ stimmt diese Näherung mit $H(X)$ überein.

$\text{Beispiel 3:}$ Wir kommen auf unser „Würfel–Experiment” zurück. Die folgende Tabelle zeigt die Wahrscheinlichkeitsfunktionen $P_R(R)$ und $P_B(B)$ für den roten und den blauen Würfel sowie die Näherungen $Q_R(R)$ und $Q_B(B)$, jeweils basierend auf dem Zufallsexperiment mit $N = 18$ Würfen. Die relativen Häufigkeiten $Q_R(R)$ und $Q_B(B)$ ergeben sich aus den beispielhaften Zufallsfolgen von $\text{Beispiel 1}$.

Wahrscheinlichkeitsfunktionen unseres Würfelexperiments

Für die Zufallsgröße $R$ gilt mit dem Logarithmus dualis $($zur Basis $2)$:

$$H(R) = H(R) \big \vert_{N \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} = \sum_{\mu = 1}^{6} 1/6 \cdot {\rm log}_2 \hspace{0.1cm} (6) = {\rm log}_2 \hspace{0.1cm} (6) = 2.585\ {\rm bit} \hspace{0.05cm},$$

$$H(R) \big \vert_{N \hspace{0.05cm} = \hspace{0.05cm}18} = 2 \cdot \frac{2}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{2} \hspace{0.1cm} +\hspace{0.1cm} 2 \cdot \frac{3}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{3} \hspace{0.1cm} +\hspace{0.1cm} 2 \cdot \frac{4}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{4} \hspace{0.1cm}= 2.530\ {\rm bit} \hspace{0.05cm}.$$

Der blaue Würfel hat natürlich die gleiche Entropie: $H(B) = H(R) = 2.585\ \rm bit$. Hier erhält man für die auf $N = 18$ basierende Näherung einen etwas größeren Wert, da nach obiger Tabelle $Q_B(B)$ von der diskreten Gleichverteilung $P_B(B)$ weniger abweicht als $Q_R(R)$ von $P_R(R)$.

$$H(B) \big \vert_{N \hspace{0.05cm} = \hspace{0.05cm}18} = 1 \cdot \frac{2}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{2} \hspace{0.1cm} +\hspace{0.1cm} 4 \cdot \frac{3}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{3} \hspace{0.1cm} +\hspace{0.1cm} 1 \cdot \frac{4}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{4} \hspace{0.1cm}= 2.558\ {\rm bit} \hspace{0.05cm}.$$

Man erkennt aus den angegebenen Zahlenwerten, dass trotz des eigentlich viel zu kleinen Experimentenparameters $N$ die Verfälschungen hinsichtlich der Entropie nicht sehr groß sind.

Es soll nochmals erwähnt werden, dass bei endlichem $N$ stets gilt:

$$ H(R) \big \vert_{N } < H(R) = {\rm log}_2 \hspace{0.1cm} (6) \hspace{0.05cm}, \hspace{0.5cm} H(B) \big \vert_{N } < H(B) = {\rm log}_2 \hspace{0.1cm} (6)\hspace{0.05cm}.$$

Relative Entropie – Kullback–Leibler–Distanz

Wir betrachten zwei Wahrscheinlichkeitsfunktionen $P_X(·)$ und $P_Y(·)$ über dem gleichen Alphabet $X = \{ x_1, \ x_2$, ... , $x_M \}$, und definieren nun folgende Größe:

$\text{Definition:}$ Die relative Entropie (englisch: Informational Divergence) zwischen den durch $P_X(·)$ und $P_Y(·)$ definierten Zufallsgrößen ist wie folgt gegeben:

$$D(P_X \hspace{0.05cm} \vert \vert \hspace{0.05cm}P_Y) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{P_X(X)}{P_Y(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{M} P_X(x_{\mu}) \cdot {\rm log} \hspace{0.1cm} \frac{P_X(x_{\mu})}{P_Y(x_{\mu})} \hspace{0.05cm}.$$

Man bezeichnet $D(P_X \vert \vert P_Y)$ auch als die Kullback–Leibler–Distanz (oder kurz: KL–Distanz).

Diese liefert ein Maß für die „Ähnlichkeit” zwischen den beiden Wahrscheinlichkeitsfunktionen $P_X(·)$ und $P_Y(·)$.

Bei Verwendung des Logarithmus zur Basis $2$ ist wieder die Pseudo–Einheit „bit” hinzuzufügen.

In ähnlicher Weise lässt sich auch eine zweite Variante der Kullback–Leibler–Distanz angeben:

$$D(P_Y \hspace{0.05cm} || \hspace{0.05cm}P_X) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{P_Y(X)}{P_X(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{M} P_Y(x_{\mu}) \cdot {\rm log} \hspace{0.1cm} \frac{P_Y(x_{\mu})}{P_X(x_{\mu})} \hspace{0.05cm}.$$

Gegenüber der ersten Variante wird nun jede Funktion $P_X(·)$ durch $P_Y(·)$ ersetzt und umgekehrt. Da sich im allgemeinen $D(P_X || P_Y)$ und $D(P_Y || P_X)$ unterscheiden, ist der Begriff „Distanz” eigentlich irreführend. Wir wollen es aber bei dieser Namensgebung belassen.

Wertet man die beiden obigen Gleichungen aus, so erkennt man folgende Eigenschaften:

Liegt die gleiche Verteilung vor ⇒ $P_Y(·) ≡ P_X(·)$, so ist $D(P_X || P_Y) = 0$. In allen anderen Fällen ist $D(P_X || P_Y) > 0$. Gleiches gilt für die Variante $D(P_Y || P_X)$.
Gilt $P_X(x_μ) ≠ 0$ und $P_Y(x_μ) = 0$ $($hierfür genügt ein einziges und beliebiges $μ)$, so ergibt sich für die Kullback–Leibler–Distanz $D(P_X || P_Y)$ ein unendlich großer Wert. In diesem Fall ist $D(P_Y || P_X)$ nicht notwendigerweise ebenfalls unendlich.
Diese Aussage macht nochmals deutlich, dass im allgemeinen $D(P_X || P_Y)$ ungleich $D(P_Y || P_X)$ sein wird.

Anschließend werden diese beiden Definitionen an unserem Standardbeispiel „Würfel–Experiment„ verdeutlicht. Gleichzeitig verweisen wir auf folgende Aufgaben:

$\text{Beispiel 4:}$ Für das Würfel–Experiment haben wir die Wahrscheinlichkeitsfunktionen $P_R(·)$ und $P_B(·)$ sowie deren Näherungen $Q_R(·)$ und $Q_B(·)$ definiert.

Die Zufallsgröße $R$ mit der PMF $P_R(·)$ gibt die Augenzahl des roten Würfels an und $B$ mit der PMF $P_B(·)$ die Augenzahl des blauen Würfels.
Die Näherungen $Q_R(·)$ und $Q_B(·)$ ergeben sich aus dem früher beschriebenen Experiment mit $N = 18$ Doppelwürfen ⇒ $\text{Beispiel 1}$ .

Wahrscheinlichkeitsfunktionen unseres Würfelexperiments

Dann gilt:

Da $P_R(·)$ und $P_B(·)$ identisch sind, erhält man für die oben definierten Kullback–Leibler–Distanzen $D(P_R \vert \vert P_B)$ und $D(P_B \vert \vert P_R)$ jeweils den Wert Null.
Der Vergleich von $P_R(·)$ und $Q_R(·)$ ergibt für die erste Variante der Kullback–Leibler–Distanz:

$$\begin{align*}D(P_R \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_R) & = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_R(\cdot)}{Q_R(\cdot)}\right ] \hspace{0.1cm} = \sum_{\mu = 1}^{6} P_R(r_{\mu}) \cdot {\rm log} \hspace{0.1cm} \frac{P_R(r_{\mu})}{Q_R(r_{\mu})} = \\ & = {1}/{6} \cdot \left [ 2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1/6}{2/18} \hspace{0.1cm} + 2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1/6}{3/18} \hspace{0.1cm} + 2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1/6}{4/18} \hspace{0.1cm} \right ] = 1/6 \cdot \big [ 2 \cdot 0.585 + 2 \cdot 0 - 2 \cdot 0.415 \big ] \approx 0.0570\ {\rm bit} \hspace{0.05cm}.\end{align*}$$

Hierbei wurde bei der vorzunehmenden Erwartungswertbildung die Tatsache ausgenutzt, dass wegen $P_R(r_1) = $ ... $ = P_R(r_6)$ der Faktor $1/6$ ausgeklammert werden kann. Da hier der Logarithmus zur Basis $ 2$ verwendet wurde, ist die Pseudo–Einheit „bit” angefügt.

Für die zweite Variante der Kullback–Leibler–Distanz ergibt sich ein etwas anderer Wert:

$$\begin{align*}D(Q_R \hspace{0.05cm}\vert \vert \hspace{0.05cm} P_R) & = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{Q_R(\cdot)}{P_R(\cdot)}\right ] \hspace{0.1cm} = \sum_{\mu = 1}^{6} Q_R(r_{\mu}) \cdot {\rm log} \hspace{0.1cm} \frac{Q_R(r_{\mu})}{P_R(r_{\mu})} \hspace{0.05cm} = \\ & = 2 \cdot \frac{2}{18} \cdot {\rm log}_2 \hspace{0.1cm} \frac{2/18}{1/6} \hspace{0.1cm} + 2 \cdot \frac{3}{18} \cdot {\rm log}_2 \hspace{0.1cm} \frac{3/18}{1/6} \hspace{0.1cm} + 2 \cdot \frac{4}{18} \cdot {\rm log}_2 \hspace{0.1cm} \frac{4/18}{1/6} \approx 0.0544\ {\rm bit} \hspace{0.05cm}.\end{align*}$$

Für den blauen Würfel erhält man $D(P_B \vert \vert Q_B) ≈ 0.0283 \ \rm bit$ und $D(Q_B \vert \vert P_B) ≈ 0.0271 \ \rm bit$, also etwas kleinere Kullback–Leibler–Distanzen, da sich die Approximation $Q_B(·)$ von $P_B(·)$ weniger unterscheidet als $Q_R(·)$ von $P_R(·)$.
Vergleicht man die Häufigkeiten $Q_R(·)$ und $Q_B(·)$, so erhält man $D(Q_R \vert \vert Q_B) ≈ 0.0597 \ \rm bit$ und $D(Q_B \vert \vert Q_R) ≈ 0.0608 \ \rm bit$. Hier sind die Distanzen am größten, da die Unterschiede zwischen $Q_B(·)$ und $Q_R(·)$ größer sind als zwischen $Q_R(·)$ und $P_R(·)$ oder zwischen $Q_B(·)$ und $P_B(·)$.

Verbundwahrscheinlichkeit und Verbundentropie

Für den Rest diese dritten Kapitels betrachten wir stets zwei diskrete Zufallsgrößen $X = \{ x_1, \ x_2$, ... , $x_M \}$ und $Y = \{ y_1, \ y_2$, ... , $y_K \}$, deren Wertebereiche nicht notwendigerweise übereinstimmen müssen. Das heißt: $K ≠ M$ $($in anderer Notation: $|Y| ≠ |X|)$ ist durchaus erlaubt.

Die Wahrscheinlichkeitsfunktion hat somit eine $K×M$–Matrixform mit den Elementen

$$P_{XY}(X = x_{\mu}\hspace{0.05cm}, \ Y = y_{\kappa}) = {\rm Pr} \big [( X = x_{\mu})\hspace{0.05cm}\cap \hspace{0.05cm} (Y = y_{\kappa}) \big ] \hspace{0.05cm}.$$

Als Kurzschreibweise verwenden wir $P_{XY}(X, Y)$. Die neue Zufallsgröße $XY$ beinhaltet sowohl die Eigenschaften von $X$ als auch diejenigen von $Y$.

$\text{Definition:}$ Die Verbundentropie (englisch: Joint Entropy) lässt sich mit der 2D–Wahrscheinlichkeitsfunktion $P_{XY}(X, Y)$ als Erwartungswert wie folgt darstellen:

$$H(XY) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{1}{P_{XY}(X, Y)}\right ] = \sum_{\mu = 1}^{M} \hspace{0.1cm} \sum_{\kappa = 1}^{K} \hspace{0.1cm} P_{XY}(x_{\mu}\hspace{0.05cm}, y_{\kappa}) \cdot {\rm log} \hspace{0.1cm} \frac{1}{P_{XY}(x_{\mu}\hspace{0.05cm}, y_{\kappa})} \hspace{0.05cm}.$$

Im Folgenden verwenden wir durchgehend den Logarithmus zur Basis $2$ ⇒ $\log(x) → \log_2(x)$. Der Zahlenwert ist somit mit der Pseudo–Einheit „bit” zu versehen.

Allgemein kann für die Verbundentropie die folgende obere Schranke angegegeben werden:

$$H(XY) \le H(X) + H(Y) \hspace{0.05cm}.$$

Diese Ungleichung drückt folgenden Sachverhalt aus:

Das Gleichheitszeichen gilt nur für den Sonderfall statistisch unabhängiger Zufallsgrößen, wie im folgenden $\text{Beispiel 5}$ anhand der Zufallsgrößen $R$ und $B$ demonstriert wird. Hierbei bezeichnen $R$ und $B$ wieder die Augenzahlen des roten bzw. des blauen Würfels.
Gibt es dagegen statistische Abhängigkeiten wie im $\text{Beispiel 6}$ zwischen den Zufallsgrößen $R$ und $S = R + B$, so gilt in obiger Gleichung das „<”–Zeichen:

$$H(RS) < H(R) + H(S).$$

In diesen Beispielen wird auch gezeigt, in wie weit sich die Verbundentropien $H(RB)$ und $H(RS)$ ändern, wenn man beim Würfel–Experiment nicht unendlich viele Wurfpaare ermittelt, sondern lediglich $N = 18$.

2D–PMF $P_{RB}$ und Näherung $Q_{RB}$

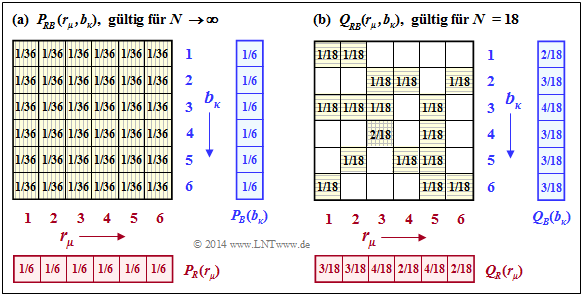
$\text{Beispiel 5:}$ Wir kommen wieder auf das Würfel–Experiment zurück:

Die Zufallsgrößen sind die Augenzahlen des

roten Würfels ⇒ $R = \{1, \ 2,\ 3,\ 4,\ 5,\ 6\}$,
blauen Würfels: ⇒ $B = \{1,\ 2,\ 3,\ 4,\ 5,\ 6\}$.

Die linke Grafik zeigt die Wahrscheinlichkeiten $P_{RB}(·)$, die sich für alle $μ = 1$, ... , $6$ und für alle $κ = 1$, ... , $6$ gleichermaßen zu $1/36$ ergeben.

Damit erhält man für die Verbundentropie:

$$H(RB) = H(RB) \big \vert_{N \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} = {\rm log}_2 \hspace{0.1cm} (36) = 5.170\ {\rm bit} \hspace{0.05cm}.$$

Man erkennt aus der linken Grafik und der hier angegebenen Gleichung:

Da $R$ und $B$ statistisch voneinander unabhängig sind, gilt

$$P_{RB}(R, B) = P_R(R) · P_B(B).$$

Die Verbundentropie ist die Summe der beiden Einzelentropien:

$$H(RB) = H(R) + H(B).$$

Die rechte Grafik zeigt die angenäherte 2D–PMF $Q_{RB}(·)$, basierend auf den nur $N = 18$ Wurfpaaren unseres Experiments. Hier ergibt sich keine quadratische Form der Verbundwahrscheinlichkeit $Q_{RB}(·)$, und die daraus abgeleitete Verbundentropie ist deutlich kleiner als $H(RB)$:

$$H(RB) \big \vert_{N \hspace{0.05cm} = \hspace{0.05cm}18} = 16 \cdot \frac{1}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{1} \hspace{0.1cm} +\hspace{0.1cm} 1 \cdot \frac{2}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{2} \hspace{0.1cm}= 4.059\ {\rm bit} \hspace{0.05cm}.$$

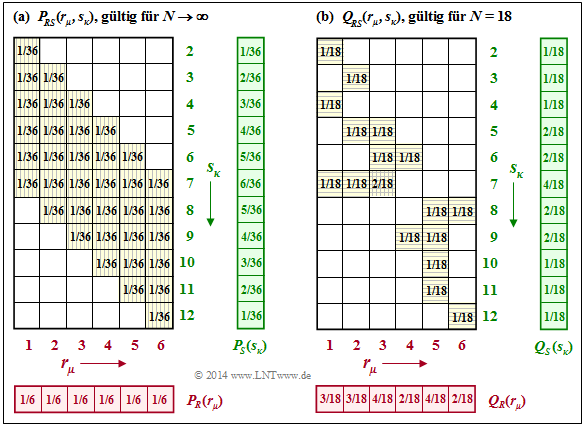
$\text{Beispiel 6:}$ Beim Würfel–Experiment haben wir neben den Zufallsgrößen $R$ (roter Würfel) und $B$ (blauer Würfel) auch die Summe $S = R + B$ betrachtet. Die linke Grafik zeigt, dass man die 2D–Wahrscheinlichkeitsfunktion $P_{RS}(·)$ nicht als Produkt von $P_R(·)$ und $P_S(·)$ schreiben kann.

Mit den Wahrscheinlichkeitsfunktionen

$$P_R(R) = \big [ \hspace{0.02cm} 1/6\hspace{0.05cm},\ 1/6\hspace{0.05cm},\ 1/6\hspace{0.05cm},\ 1/6\hspace{0.05cm},\ 1/6\hspace{0.05cm},\ 1/6 \hspace{0.02cm} \big ] \hspace{0.05cm},$$

$$P_S(S)=\big [ \hspace{0.02cm} 1/36\hspace{0.05cm},\ 2/36\hspace{0.05cm},\ 3/36\hspace{0.05cm},\ 4/36\hspace{0.05cm},\ 5/36\hspace{0.05cm},\ 6/36\hspace{0.05cm},\ 5/36\hspace{0.05cm},\ 4/36\hspace{0.05cm},\ 3/36\hspace{0.05cm},\ 2/36\hspace{0.05cm},\ 1/36\hspace{0.02cm} \big ] \hspace{0.05cm}$$

erhält man für die Entropien:

$$H(S) = 2 \hspace{-0.05cm}\cdot \hspace{-0.05cm}\frac{1}{36} \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2 \hspace{0.05cm} \frac{36}{1} \hspace{0.05cm} + 2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{2}{36} \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2 \hspace{0.05cm} \frac{36}{2} \hspace{0.05cm} + 2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{3}{36} \cdot {\rm log}_2 \hspace{0.05cm} \frac{36}{3} \hspace{0.05cm} + 2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{4}{36} \cdot {\rm log}_2 \hspace{0.05cm} \frac{36}{4} \hspace{0.05cm} +2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{5}{36} \cdot {\rm log}_2 \hspace{0.05cm} \frac{36}{5} + 1 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{6}{36} \cdot {\rm log}_2 \hspace{0.05cm} \frac{36}{6} \approx 3.274\ {\rm bit} \hspace{0.05cm}, $$

$$H(R) = {\rm log}_2 \hspace{0.1cm} (6) \approx 2.585\ {\rm bit} \hspace{0.05cm},\hspace{1.05cm} H(RS) = {\rm log}_2 \hspace{0.1cm} (36) \approx 5.170\ {\rm bit} \hspace{0.05cm}.$$

2D–PMF $P_{RS}$ und Näherung $Q_{RS}$

Aus diesen Zahlenwerten erkennt man:

Aufgrund der statistischen Abhängigkeit zwischen dem roten Würfel und der Summe ist die Verbundentropie

$$H(RS) ≈ 5.170 \ \rm bit < H(R) + H(S) ≈ 5.877 \ \rm bit.$$

Der Vergleich mit $\text{Beispiel 5}$ zeigt, dass $H(RS) =H(RB)$ ist.
Der Grund hierfür ist, dass bei Kenntnis von $R$ die Zufallsgrößen $B$ und $S$ genau die gleichen Informationen liefern.

Rechts dargestellt ist der Fall, dass die 2D–PMF $Q_{RS}(·)$ empirisch ermittelt wurde $(N = 18)$. Obwohl sich aufgrund des sehr kleinen $N$–Wertes ein völlig anderes Bild ergibt, liefert die Näherung für $H(RS)$ den exakt gleichen Wert wie die Näherung für $H(RB)$ im $\text{Beispiel 5}$:

$$H(RS) \big \vert_{N \hspace{0.05cm} = \hspace{0.05cm}18} = H(RB) \big \vert_{N \hspace{0.05cm} = \hspace{0.05cm}18} = 4.059\,{\rm bit} \hspace{0.05cm}.$$