Some Preliminary Remarks on Two-Dimensional Random Variables

1 # OVERVIEW OF THE THIRD MAIN CHAPTER #
2 Introductory example on the statistical dependence of random variables
3 Prerequisites and nomenclature
4 Probability function and probability density function
5 Probability function and entropy
6 Informational Divergence - Kullback-Leibler Distance
7 Joint probability and joint entropy
8 Relevant tasks
9 Quellenverzeichnis

# OVERVIEW OF THE THIRD MAIN CHAPTER #

The focus of this third main chapter is the mutual information $I(X; Y)$ between two random variables $X$ and $Y$. With statistical dependence, $I(X; Y)$ is smaller than the individual entropies $H(X)$ or $H(Y)$. For example, the uncertainty regarding the random variable $X$ ⇒ entropy $H(X)$ is reduced by the knowledge of $Y$ , by the amount $H(X\hspace{0.03cm}|\hspace{0.03cm}Y)$ ⇒ conditional entropy of $X$, falls $Y$ is known. The remaining residue is the mutual information $I(X; Y)$. At the same time, however $I(X; Y) = H(Y) - H(Y\hspace{0.03cm}|\hspace{0.03cm}X)$. The semicolon indicates that the two random variables under consideration, $X$ and $Y$ , are equal.

In detail, the third main chapter deals with:

the relationship between probability and entropy for 2D random variables,
the calculation of the informational divergence, , also known as the Kullback–Leibler distance ,
the definition of the joint entropy $H(XY)$ and the conditional entropies $H(X\hspace{0.03cm}|\hspace{0.03cm}Y)$ and $H(Y\hspace{0.03cm}|\hspace{0.03cm}X)$,
the mutual information $I(X; Y)$ between two random variables ,
the information theory of digital signal transmission and the corresponding model,
the definition and meaning of the channel capacity and its connection with the mutual information,
the capacity calculation for digital memoryless channels such as BSC, BEC and BSEC,
the channel coding theorem, one of the highlights of Shannon's information theory.

Further information on the topic as well as tasks, simulations and programming exercises can be found in the experiment „Wertdiskrete Informationstheorie” of the practical course „Simulation Digitaler Übertragungssysteme ”. This (former) LNT course at the TU Munich is based on

the windows programme WDIT ⇒ link refers to the ZIP version of the programme; and
the corresponding Praktikumsanleitung ⇒ link refers to the PDF version.

Introductory example on the statistical dependence of random variables

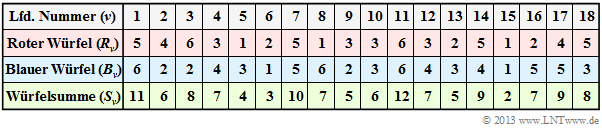
$\text{Example 1:}$ We start from the experiment „rolling two dice” aus, where both dice are distinguishable (by colour). The table shows the results of the first $N = 18$ pairs of throws of this exemplary random experiment.

Result protocol of our random experiment „throwing two dice”

Note: According to the nomenclature explained in the following section r $R_ν$, $B_ν$ and $S_ν$ are to be understood as random variables here:

For example, the random variable $R_3 \in \{1, \ 2, \ 3, \ 4, \ 5, \ 6\}$ indicates the number of eyes of the red die on the third throw as a probability event. The specification $R_3 = 6$ states that in the documented realisation the red die showed a „6” in the third throw.

In line 2, the numbers of the red die $(R)$ are indicated. The mean value of this limited sequence $〈R_1$, ... , $R_{18}〉$ is with $3.39$ smaller than the expected value ${\rm E}\big[R\big] = 3.5$. Line 3 shows the numbers of eyes of the blue cube $(B)$. The sequence $〈B_1$, ... , $B_{18}〉$ has a slightly larger mean value of $3.61$ einen has a slightly larger mean value of ⇒ ${\rm E}\big[B\big] = 3.5$.
Line 4 contains the sum $S_ν = R_ν + B_ν$. The mean value of the sequence $〈S_1$, ... , $S_{18}〉$ is $3.39 + 3.61 = 7$. This is here (by chance) equal to the expected value $\text{E}\big[S\big] = \text{E}\big[R\big] + \text{E}\big[B\big]$.

Now the question arises between which random variables there are statistical dependencies:

If one assumes fair dice, there are no statistical ties between the sequences $〈 R\hspace{0.05cm} 〉$ and $〈B \hspace{0.05cm}〉$ – whether bounded or unbounded: Even if one knows $R_ν$ for $B_ν$ all possible numbers of eyes $1$, ... , $6$ are equally probable.
If one knows $S_ν$, however, statements about $R_ν$ as well as about $B_ν$ are possible. From $S_{11} = 12$ follows directly $R_{11} = B_{11} = 6$ and the sum $S_{15} = 2$ of two dice is only possible with two ones. Such dependencies are called deterministic.
From $S_7 = 10$ , at least ranges for $R_7$ and $B_7$ can be given: $R_7 ≥ 4, \ B_7 ≥ 4$. Then only the three pairs of values $(R_7 = 4) ∩ (B_7 = 6)$, $(R_7 = 5) ∩ (B_7 = 5)$ as well as $(R_7 = 6) ∩ (B_7 = 4)$ are possible. Here there is no deterministic relationship between the random variables $S_ν$ and $R_ν$ $($or. $B_ν)$, but rather a so-called statistical dependence.
Such statistical dependencies exist for $S_ν ∈ \{3, \ 4, \ 5, \ 6, \ 8, \ 9, \ 10, \ 11\}$. If, on the other hand, the sum $S_ν = 7$, one cannot infer $R_ν$ and $B_ν$ from this. For both dice, all possible numbers $1$, ... , $6$ are equally probable. In this case, there are also no statistical ties between $S_ν$ and $R_ν$ or between $S_ν$ and $B_ν$.

Prerequisites and nomenclature

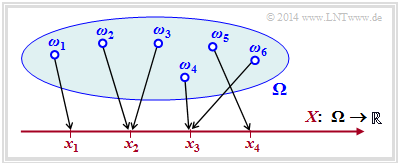
Throughout this chapter, we consider discrete-value random variables of the form $X = \{ x_1, \ x_2, \hspace{0.05cm}$ ... $\hspace{0.05cm},\ x_{\mu},\hspace{0.05cm}$ ... $\hspace{0.05cm},\ x_M \} \hspace{0.05cm},$ , and use the following nomenclature:

The random variable itself is always denoted by a capital letter. The lower case letter $x$ indicates a possible realisation of the random variable $X$ .
All realisations $x_μ$ $($with $μ = 1$, ... , $M)$ are real-valued. $M$ indicates the symbol set size of of $X$ . Instead of $M$ , we sometimes also use $|X|$.

Relationship between the probability space ${\it \Omega}$
and the random variable $X$

The random variable $X$ can, for example, be created by the transformation $\Omega → X$ , where $\Omega$ stands for the probability space of a random experiment.

The diagram illustrates such a transformation:

$${\it \Omega} = \{ \omega_1, \omega_2, \omega_3, ... \hspace{0.15cm} \} \hspace{0.25cm} \longmapsto \hspace{0.25cm} X = \{ x_1, \ x_2, \ x_3, \ x_4\} \subset \cal{R}\hspace{0.05cm}.$$

Each random event $ω_i ∈ Ω$ is uniquely assigned to a real numerical value $x_μ ∈ X ⊂ ℝ$ .
In the example considered, the running variable is $1 ≤ μ ≤ 4$, , i.e. the symbol range is $M = |X| = 4$.
However, the figure is not one-to-one: the realisation $x_3 ∈ X$ could have resulted from the elementary event $ω_4$ in the example, but also from $ω_6$ $($or from some other of the infinitely many elementary events $ω_i$ not drawn in the diagram).

$\text{Agreement:}$ Often one refrains from indexing both the elementary events $ω_i$ and the realisations $x_μ$. This results in the following shorthand notations, for example:

$$ \{ X = x \} \hspace{0.05cm} \equiv \hspace{0.05cm} \{ \omega \in {\it \Omega} : \hspace{0.4cm} X(\omega) = x \} \hspace{0.05cm},$$

$$ \{ X \le x \} \hspace{0.05cm} \equiv \hspace{0.05cm} \{ \omega \in {\it \Omega} : \hspace{0.4cm} X(\omega) \le x \} \hspace{0.05cm}.$$

With this agreement, the probabilities of the discrete random variable $X$ are:

$${\rm Pr}( X = x_{\mu}) = \hspace{-0.2cm} \sum_{\omega \hspace{0.1cm} \in \{ X = x_{\mu} \} } \hspace{-0.2cm}{\rm Pr} \left ( \{ \omega \} \right ) \hspace{0.05cm}.$$

Probability function and probability density function

$\text{Definition:}$ If the $M$ probabilities of a discrete random variable $X$ ⇒ ${\rm Pr}( X = x_{\mu})$ are combined in a similar way to a vector, we arrive at the probability mass function ( PMF):

$$P_X(X) = \big [ \hspace{0.02cm} P_X(x_1), P_X(x_2), \hspace{0.05cm}\text{...} \hspace{0.15cm}, P_X(x_{\mu}),\hspace{0.05cm} \text{...}\hspace{0.15cm}, P_X(x_M) \hspace{0.02cm} \big ] \hspace{0.05cm}.$$

The $μ$–element of this „vector” indicates the probability $P_X(x_{\mu}) = {\rm Pr}( X = x_{\mu}) $ an.

In the book„Stochastische Signaltheorie” , we defined a similar descriptive quantity with the Probability Density Function $($ PDF$)$ and designated it as $f_X(x)$ bezeichnet.

It should be noted, however:

The PDF is more suitable for characterising continuous random variables, such as a Gaussian distribution or a uniform distribution. Only through the use of Dirac functions does the PDF also become applicable for discrete random variables.
The PMF provides less information about the random variable than the PDF and can also only be specified for discrete variables. However, for the discrete value information theory considered in this chapter, the PMF is sufficient.

$\text{Example 2:}$ We consider a probability density function (PDF) without much practical relevance:

$$f_X(x) = 0.2 \cdot \delta(x+2) + 0.3 \cdot \delta(x - 1.5)+0.5 \cdot \delta(x - {\rm \pi}) \hspace{0.05cm}. $$

Thus, for the discrete random variable, $x ∈ X = \{–2,\ +1.5,\ +\pi \} $ ⇒ symbol range $M = \vert X \vert = 3$, and the probability function (PMF) is:

$$P_X(X) = \big [ \hspace{0.1cm}0.2\hspace{0.05cm}, 0.3\hspace{0.05cm}, 0.5 \hspace{0.1cm} \big] \hspace{0.05cm}. $$

It can be seen:

The PMF only provides information about the probabilities $\text{Pr}(x_1)$, $\text{Pr}(x_2)$ and $\text{Pr}(x_3)$.
From the PDF , on the other hand, the possible realisations $x_1$, $x_2$ and $x_3$ of the random variable $X$ can also be read.
The only requirement for the random variable is that it is real-valued.
The possible values $x_μ$ do not have to be positive, integer, equidistant or rational.

Probability function and entropy

In discrete value information theory, in contrast to transmission problems, knowledge of the probability function $P_X(X)$ is sufficient, for example, to calculate entropy.

$\text{Definition:}$ The entropy of a discrete random variable $X$ – i.e. its uncertainty for an observer - can be represented with the probability function $P_X(X)$ as follows:

$$H(X) = {\rm E} \big [ {\rm log} \hspace{0.1cm} \frac{1}{P_X(X)}\big ] \hspace{0.05cm}=\hspace{0.05cm} - {\rm E} \big [ {\rm log} \hspace{0.1cm} {P_X(X)}\big ] \hspace{0.05cm}=\hspace{0.05cm} \sum_{\mu = 1}^{M} P_X(x_{\mu}) \cdot {\rm log} \hspace{0.1cm} \frac{1}{P_X(x_{\mu})} \hspace{0.05cm}=\hspace{0.05cm} - \sum_{\mu = 1}^{M} P_X(x_{\mu}) \cdot {\rm log} \hspace{0.1cm} {P_X(x_{\mu})} \hspace{0.05cm}.$$

If one uses the logarithm to the base $2$, i.e. $\log_2$ (...) ⇒ binary logarithm, the numerical value is provided with the pseudo-unit „bit” . $\rm E\big[$...$\big]$ indicates the expected value.

For example, one obtains

für $P_X(X) = \big [\hspace{0.02cm}0.2, \ 0.3, \ 0.5 \hspace{0.02cm}\big ]$:

$$H(X) = 0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} + 0.3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.3} +0.5 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.5} \approx 1.485\,{\rm bit}\hspace{0.05cm},$$

für $P_X(X) = \big [\hspace{0.02cm}1/3, \ 1/3, \ 1/3\hspace{0.02cm}\big ]$:

$$H(X) = 3 \cdot 1/3 \cdot {\rm log}_2 \hspace{0.1cm} (3) = {\rm log}_2 \hspace{0.1cm} (3) \approx 1.585\,{\rm bit}\hspace{0.05cm}.$$

The second example provides the maximum of the entropy function for the symbol range $M = 3$.

$\text{Derivation:}$ For a general $M$ for example, this result can be derived as follows – see [Meck]^[1]:

$$H(X) = -{\rm E} \big [ {\rm log} \hspace{0.1cm} {P_X(X)}\big ] \hspace{0.2cm} \le \hspace{0.2cm}- {\rm log} \big [ {\rm E} \hspace{0.1cm} \left [{P_X(X)}\right ] \big ] \hspace{0.05cm}.$$

This estimation $($Jensens's inequality$)$ is admissible because the logarithm is a concave function. According to task 3.2 , the following holds:

$$- {\rm E} \big [ {P_X(X)}\big ] \hspace{0.1cm} \le \hspace{0.1cm} M \hspace{0.3cm} \Rightarrow \hspace{0.3cm} H(X) \le {\rm log} \hspace{0.1cm} (M) \hspace{0.05cm}.$$

The equal sign results according to the calculation above for equal probabilities, i.e. for $P_X(x_μ) = {1}/{M}$ for all $μ$. In task 3.3 , the same situation is to be solved using the estimate

$${\rm ln} \hspace{0.1cm} (x) \le x-1$$

is to be proved. The equal sign applies here only for $x = 1$.

If one of the $M$ probabilities $P_X(x_μ)$ of the probability function is equal to zero, a tighter bound can be given for the entropy:

$$H(X) \le {\rm log} \hspace{0.1cm} (M-1) \hspace{0.05cm}.$$

$\text{Agreement:}$ In the following example and on the next pages we use the following nomenclature:

The entropy $H(X)$ always refers to the actual probability function $P_X(X)$ of the discrete random variable. Experimentally, these quantities are obtained only after $N → ∞$ trials.
If the probability function is determined from a finite random sequence, we denote this probability function by $Q_X(X)$ and add „$N =$ ...” to the resulting entropy.
This entropy approximation is not based on probabilities, but only on the relative frequencies. Only for $N → ∞$ does this approximation agree with $H(X)$ .

$\text{Example 3:}$ We return to our „dice experiment” . The following table shows the probability functions $P_R(R)$ and $P_B(B)$ for the red and blue dice as well as the approximations $Q_R(R)$ and $Q_B(B)$, in each case based on the random experiment with $N = 18$ throws. The relative frequencies $Q_R(R)$ and $Q_B(B)$ result from the exemplary random sequences of $\text{example 1}$.

Probability functions of our dice experiment

The following applies to the random variable $R$ with the binary logarithm $($to base $2)$:

$$H(R) = H(R) \big \vert_{N \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} = \sum_{\mu = 1}^{6} 1/6 \cdot {\rm log}_2 \hspace{0.1cm} (6) = {\rm log}_2 \hspace{0.1cm} (6) = 2.585\ {\rm bit} \hspace{0.05cm},$$

$$H(R) \big \vert_{N \hspace{0.05cm} = \hspace{0.05cm}18} = 2 \cdot \frac{2}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{2} \hspace{0.1cm} +\hspace{0.1cm} 2 \cdot \frac{3}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{3} \hspace{0.1cm} +\hspace{0.1cm} 2 \cdot \frac{4}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{4} \hspace{0.1cm}= 2.530\ {\rm bit} \hspace{0.05cm}.$$

The blue cube of course has the same entropy: $H(B) = H(R) = 2.585\ \rm bits$. Here we get a slightly larger value for the approximation based on $N = 18$ , since according to the table above $Q_B(B)$ deviates less from the discrete uniform distribution $P_B(B)$ than als $Q_R(R)$ from $P_R(R)$.

$$H(B) \big \vert_{N \hspace{0.05cm} = \hspace{0.05cm}18} = 1 \cdot \frac{2}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{2} \hspace{0.1cm} +\hspace{0.1cm} 4 \cdot \frac{3}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{3} \hspace{0.1cm} +\hspace{0.1cm} 1 \cdot \frac{4}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{4} \hspace{0.1cm}= 2.558\ {\rm bit} \hspace{0.05cm}.$$

It can be seen from the given numerical values that despite the experimental parameter $N$ , which is actually much too small, the distortions with regard to entropy are not very large.

It should be mentioned again that with finite $N$ , the following always applies:

$$ H(R) \big \vert_{N } < H(R) = {\rm log}_2 \hspace{0.1cm} (6) \hspace{0.05cm}, \hspace{0.5cm} H(B) \big \vert_{N } < H(B) = {\rm log}_2 \hspace{0.1cm} (6)\hspace{0.05cm}.$$

Informational Divergence - Kullback-Leibler Distance

We consider two probability functions $P_X(·)$ and $P_Y(·)$ over the same alphabet $X = \{ x_1, \ x_2$, ... , $x_M \}$, is given as follows:

$\text{Definition:}$ The Informational Divergence between the random variables defined by $P_X(·)$ and $P_Y(·)$ is given as follows:

$$D(P_X \hspace{0.05cm} \vert \vert \hspace{0.05cm}P_Y) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{P_X(X)}{P_Y(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{M} P_X(x_{\mu}) \cdot {\rm log} \hspace{0.1cm} \frac{P_X(x_{\mu})}{P_Y(x_{\mu})} \hspace{0.05cm}.$$

$D(P_X \vert \vert P_Y)$ is also called Kullback–Leibler distance .

This provides a measure of the „similarity” between the two probability functions $P_X(·)$ and $P_Y(·)$.

When using the logarithm to base $2$ the pseudo-unit „bit” must again be added.

ISimilarly, a second variant of the Kullback-Leibler distance can be given:

$$D(P_Y \hspace{0.05cm} || \hspace{0.05cm}P_X) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{P_Y(X)}{P_X(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{M} P_Y(x_{\mu}) \cdot {\rm log} \hspace{0.1cm} \frac{P_Y(x_{\mu})}{P_X(x_{\mu})} \hspace{0.05cm}.$$

Compared to the first variant, each function $P_X(·)$ is now replaced by $P_Y(·)$ and vice versa. Since in general $D(P_X || P_Y)$ and $D(P_Y || P_X)$ differ, the term „distance” is actually misleading. However, we want to leave it at this naming.

If we evaluate the two equations above, we recognise the following properties:

If the same distribution is present ⇒ $P_Y(·) ≡ P_X(·)$, then $D(P_X || P_Y) = 0$. In all other cases $D(P_X || P_Y) > 0$. The same applies to the variant $D(P_Y || P_X)$.
If $P_X(x_μ) ≠ 0$ and $P_Y(x_μ) = 0$ $($a single and arbitrary $μ is sufficient for this)$,the Kullback-Leibler distance $D(P_X || P_Y)$ has an infinitely large value. In this case, $D(P_Y || P_X)$ is not necessarily infinite either.
This statement makes it clear once again that in general $D(P_X || P_Y)$ will be unequal to $D(P_Y || P_X)$ .

Subsequently, these two definitions are clarified with our standard example „dice experiment„ . At the same time we refer to the following tasks:

$\text{Example 4:}$ For the dice experiment, we have defined the probability functions $P_R(·)$ and $P_B(·)$ and their approximations $Q_R(·)$ and $Q_B(·)$ .

The random variable $R$ with the PMF $P_R(·)$ indicates the numbers of the red die and $B$ mit der PMF $P_B(·)$ the numbers of the blue cube.
The approximations $Q_R(·)$ and $Q_B(·)$ result from the experiment described earlier with $N = 18$ double throws ⇒ $\text{Example 1}$ .

Probability functions of our dice experiment

Then holds:

Since $P_R(·)$ and $P_B(·)$ are identical, we obtain zero for each of the Kullback-Leibler distances $D(P_R \vert \vert P_B)$ and $D(P_B \vert \vert P_R)$ defined above.
The comparison of $P_R(·)$ and $Q_R(·)$ yields for the first variant of the Kullback-Leibler distance:

$$\begin{align*}D(P_R \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_R) & = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_R(\cdot)}{Q_R(\cdot)}\right ] \hspace{0.1cm} = \sum_{\mu = 1}^{6} P_R(r_{\mu}) \cdot {\rm log} \hspace{0.1cm} \frac{P_R(r_{\mu})}{Q_R(r_{\mu})} = \\ & = {1}/{6} \cdot \left [ 2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1/6}{2/18} \hspace{0.1cm} + 2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1/6}{3/18} \hspace{0.1cm} + 2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1/6}{4/18} \hspace{0.1cm} \right ] = 1/6 \cdot \big [ 2 \cdot 0.585 + 2 \cdot 0 - 2 \cdot 0.415 \big ] \approx 0.0570\ {\rm bit} \hspace{0.05cm}.\end{align*}$$

Here, the expected value formation to be carried out exploited the fact that due to $P_R(r_1) = $ ... $ = P_R(r_6)$ , the factor $1/6$ can be excluded. Since the logarithm to base $ 2$ was used here, the pseudo-unit „bit” was used.

For the second variant of the Kullback-Leibler distance, a slightly different value results:

$$\begin{align*}D(Q_R \hspace{0.05cm}\vert \vert \hspace{0.05cm} P_R) & = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{Q_R(\cdot)}{P_R(\cdot)}\right ] \hspace{0.1cm} = \sum_{\mu = 1}^{6} Q_R(r_{\mu}) \cdot {\rm log} \hspace{0.1cm} \frac{Q_R(r_{\mu})}{P_R(r_{\mu})} \hspace{0.05cm} = \\ & = 2 \cdot \frac{2}{18} \cdot {\rm log}_2 \hspace{0.1cm} \frac{2/18}{1/6} \hspace{0.1cm} + 2 \cdot \frac{3}{18} \cdot {\rm log}_2 \hspace{0.1cm} \frac{3/18}{1/6} \hspace{0.1cm} + 2 \cdot \frac{4}{18} \cdot {\rm log}_2 \hspace{0.1cm} \frac{4/18}{1/6} \approx 0.0544\ {\rm bit} \hspace{0.05cm}.\end{align*}$$

For the blue cube, one obtains $D(P_B \vert \vert Q_B) ≈ 0.0283 \ \rm bit$ and $D(Q_B \vert \vert P_B) ≈ 0.0271 \ \rm bit$, i.e. slightly smaller Kullback-Leibler distances, since the approximation $Q_B(·)$ of $P_B(·)$ differs less than $Q_R(·)$ of $P_R(·)$.
Comparing the frequencies $Q_R(·)$ and $Q_B(·)$, we get $D(Q_R \vert \vert Q_B) ≈ 0.0597 \ \rm bit$ and $D(Q_B \vert \vert Q_R) ≈ 0.0608 \ \rm bit$. Here the distances are greatest, since the differences between $Q_B(·)$ and $Q_R(·)$ are greater than between $Q_R(·)$ and $P_R(·)$ or between $Q_B(·)$ and $P_B(·)$.

Joint probability and joint entropy

For the remainder of this third chapter, we always consider two discrete random variable $X = \{ x_1, \ x_2$, ... , $x_M \}$ and $Y = \{ y_1, \ y_2$, ... , $y_K \}$, whose value ranges do not necessarily have to coincide. This means: $K ≠ M$ $($in other notation: $|Y| ≠ |X|)$ is quite permissible.

The probability function thus has a $K×M$ matrix form with the elements

$$P_{XY}(X = x_{\mu}\hspace{0.05cm}, \ Y = y_{\kappa}) = {\rm Pr} \big [( X = x_{\mu})\hspace{0.05cm}\cap \hspace{0.05cm} (Y = y_{\kappa}) \big ] \hspace{0.05cm}.$$

We use $P_{XY}(X, Y)$ as a shorthand notation. The new random variable $XY$ contains both the properties of $X$ and those of $Y$.

$\text{Definition:}$ The joint entropy can be represented with the 2D probability function $P_{XY}(X, Y)$ as an expected value as follows:

$$H(XY) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{1}{P_{XY}(X, Y)}\right ] = \sum_{\mu = 1}^{M} \hspace{0.1cm} \sum_{\kappa = 1}^{K} \hspace{0.1cm} P_{XY}(x_{\mu}\hspace{0.05cm}, y_{\kappa}) \cdot {\rm log} \hspace{0.1cm} \frac{1}{P_{XY}(x_{\mu}\hspace{0.05cm}, y_{\kappa})} \hspace{0.05cm}.$$

In the following we use the logarithm to the base $2$ ⇒ $\log(x) → \log_2(x)$ throughout. The numerical value is thus to be assigned the pseudo-unit „bit”.

In general, the following upper bound can be given for the compound entropy:

$$H(XY) \le H(X) + H(Y) \hspace{0.05cm}.$$

This inequality expresses the following fact:

The equal sign only applies to the special case of statistically independent random variables, as demonstrated in the following $\text{example 5}$ using the random variables $R$ and $B$ . Here $R$ and $B$ denote the numbers of the red and blue dice, respectively.
If, on the other hand, there are statistical dependencies as in example $\text{example 6}$ between the random variables $R$ and $S = R + B$, the „<” sign applies in the above equation:

$$H(RS) < H(R) + H(S).$$

These examples also show to what extent the joint entropies $H(RB)$ and $H(RS)$ change if one does not determine an infinite number of pairs of throws in the dice experiment, but only $N = 18$.

2D–PMF $P_{RB}$ and approximation $Q_{RB}$

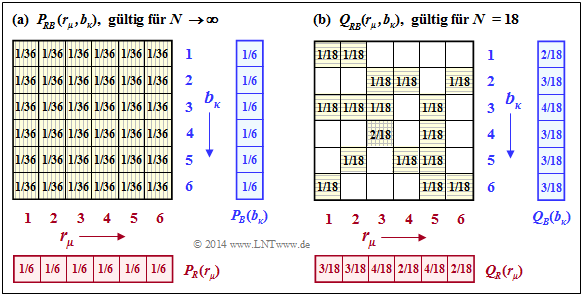
$\text{Example 5:}$ We return to the dice experiment :

The random variables are the numbers of the

red die ⇒ $R = \{1, \ 2,\ 3,\ 4,\ 5,\ 6\}$,
blue die: ⇒ $B = \{1,\ 2,\ 3,\ 4,\ 5,\ 6\}$.

The left graph shows the probabilities $P_{RB}(·)$, which are obtained for all $μ = 1$, ... , $6$ and for all $κ = 1$, ... , $6$ equally add up to $1/36$ ergeben.

Thus, one obtains for the joint entropy:

$$H(RB) = H(RB) \big \vert_{N \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} = {\rm log}_2 \hspace{0.1cm} (36) = 5.170\ {\rm bit} \hspace{0.05cm}.$$

One can see from the left graph and the equation given here:

Since $R$ and $B$ are statistically independent of each other, the following applies.

$$P_{RB}(R, B) = P_R(R) · P_B(B).$$

The joint entropy is the sum of the two individual entropies:

$$H(RB) = H(R) + H(B).$$

The right graph shows the approximated 2D–PMF $Q_{RB}(·)$, based on the only $N = 18$ throws of our experiment. Here, no quadratic form of the joint probability $Q_{RB}(·)$, results, and the joint entropy derived from it is significantly smaller than $H(RB)$:

$$H(RB) \big \vert_{N \hspace{0.05cm} = \hspace{0.05cm}18} = 16 \cdot \frac{1}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{1} \hspace{0.1cm} +\hspace{0.1cm} 1 \cdot \frac{2}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{2} \hspace{0.1cm}= 4.059\ {\rm bit} \hspace{0.05cm}.$$

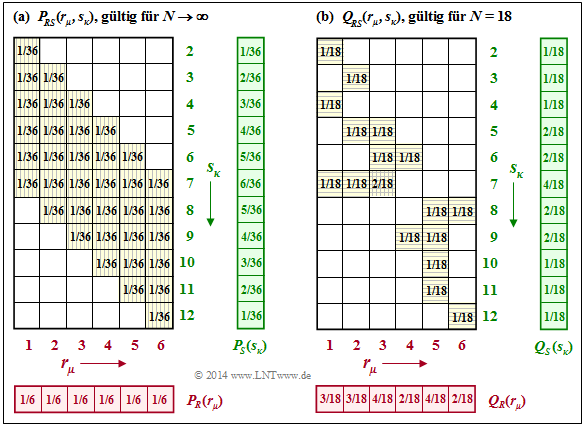
$\text{Example 6:}$ In the dice experiment, in addition to the random variables $R$ (roter Würfel) and $B$ (blue die) also the sum $S = R + B$ is considered. The graph on the left shows that the 2D probability function $P_{RS}(·)$ cannot be written as a product of $P_R(·)$ and $P_S(·)$ .

With the probability functions

$$P_R(R) = \big [ \hspace{0.02cm} 1/6\hspace{0.05cm},\ 1/6\hspace{0.05cm},\ 1/6\hspace{0.05cm},\ 1/6\hspace{0.05cm},\ 1/6\hspace{0.05cm},\ 1/6 \hspace{0.02cm} \big ] \hspace{0.05cm},$$

$$P_S(S)=\big [ \hspace{0.02cm} 1/36\hspace{0.05cm},\ 2/36\hspace{0.05cm},\ 3/36\hspace{0.05cm},\ 4/36\hspace{0.05cm},\ 5/36\hspace{0.05cm},\ 6/36\hspace{0.05cm},\ 5/36\hspace{0.05cm},\ 4/36\hspace{0.05cm},\ 3/36\hspace{0.05cm},\ 2/36\hspace{0.05cm},\ 1/36\hspace{0.02cm} \big ] \hspace{0.05cm}$$

one obtains for the entropies:

$$H(S) = 2 \hspace{-0.05cm}\cdot \hspace{-0.05cm}\frac{1}{36} \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2 \hspace{0.05cm} \frac{36}{1} \hspace{0.05cm} + 2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{2}{36} \hspace{-0.05cm}\cdot \hspace{-0.05cm} {\rm log}_2 \hspace{0.05cm} \frac{36}{2} \hspace{0.05cm} + 2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{3}{36} \cdot {\rm log}_2 \hspace{0.05cm} \frac{36}{3} \hspace{0.05cm} + 2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{4}{36} \cdot {\rm log}_2 \hspace{0.05cm} \frac{36}{4} \hspace{0.05cm} +2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{5}{36} \cdot {\rm log}_2 \hspace{0.05cm} \frac{36}{5} + 1 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \frac{6}{36} \cdot {\rm log}_2 \hspace{0.05cm} \frac{36}{6} \approx 3.274\ {\rm bit} \hspace{0.05cm}, $$

$$H(R) = {\rm log}_2 \hspace{0.1cm} (6) \approx 2.585\ {\rm bit} \hspace{0.05cm},\hspace{1.05cm} H(RS) = {\rm log}_2 \hspace{0.1cm} (36) \approx 5.170\ {\rm bit} \hspace{0.05cm}.$$

2D–PMF $P_{RS}$ and approximation $Q_{RS}$

From these numerical values one can see:

Due to the statistical dependence between the red die and the sum, the joint entropy is

$$H(RS) ≈ 5.170 \ \rm bit < H(R) + H(S) ≈ 5.877 \ \rm bit.$$

Der Vergleich mit $\text{Beispiel 5}$ zeigt, dass $H(RS) =H(RB)$ ist.
The reason for this is that if $R$ is known, the random variables $B$ and $S$ provide exactly the same information.

Shown on the right is the case where the 2D PMF $Q_{RS}(·)$ was determined empirically $(N = 18)$. Although a completely different picture emerges due to the very small $N$–value, the approximation for $H(RS)$ provides exactly the same value as the approximation for $H(RB)$ in $\text{example 5}$:

$$H(RS) \big \vert_{N \hspace{0.05cm} = \hspace{0.05cm}18} = H(RB) \big \vert_{N \hspace{0.05cm} = \hspace{0.05cm}18} = 4.059\,{\rm bit} \hspace{0.05cm}.$$