Exercise 1.3Z: Calculating with Complex Numbers II

• Return to book

Considered numbers in the complex plane

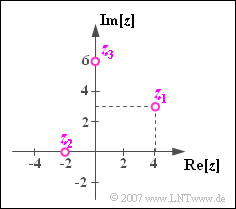
The following three complex quantities are shown in the complex plane to the right:

$$z_1 = 4 + 3\cdot {\rm j},$$

$$z_2 = -2 ,$$

$$z_3 = 6\cdot{\rm j} .$$

Within the framework of this task, the following quantities are to be calculated:

$$z_4 = z_1 \cdot z_1^{\star},$$

$$z_5 = z_1 + 2 \cdot z_2 - {z_3}/{2},$$

$$z_6 = z_1 \cdot z_2,$$

$$z_7 = {z_3}/{z_1}.$$

Hints:

• This exercise belongs to the chapter Calculating with Complex Numbers.
• The topic of this task is also covered in the (German language) learning video
       Rechnen mit komplexen Zahlen   ⇒   "Arithmetic operations involving complex numbers".
• Enter the phase values in the range of  $-\hspace{-0.05cm}180^{\circ} < \phi ≤ +180^{\circ}$.

Questions

1

Enter the magnitude and phase of  $z_1$ .

$|z_1|\ = \ $

$\phi_1\ = \ $ $\hspace{0.2cm}\text{deg}$

2

What is  $z_4 = z_1 \cdot z_1^{\star} = x_4 + \text{j} \cdot y_4$?

$x_4\ = \ $

$y_4\ = \ $

3

Calculate  $z_5 = x_5 + {\rm j} \cdot y_5$ .

$x_5\ = \ $

$y_5\ = \ $

4

Specify the magnitude and phase of  $z_6 = z_1 \cdot z_2$    $($range  $\pm 180^{\circ})$.

$|z_6|\ = \ $

$\phi_6\ = \ $ $\hspace{0.2cm}\text{deg}$

5

What is the phase value of the purely imaginary number  $z_3$?

$\phi_3 \ = \ $ $\hspace{0.2cm}\text{deg}$

6

Calculate the magnitude and phase of  $z_7 = z_3/z_1$    $($range  $\pm 180^{\circ})$.

$|z_7| \ = \ $

$\phi_7 \ = \ $ $\hspace{0.2cm}\text{deg}$

Solution

Solution

(1)  The magnitude can be calculated according to the  Pythagorean  theorem:

$$|z_1| = \sqrt{x_1^2 + y_1^2}= \sqrt{4^2 + 3^2}\hspace{0.15cm}\underline{ = 5}.$$

• For the phase angle, the following applies according to the page  Darstellung nach Betrag und Phase :

$$\phi_1 = \arctan \frac{y_1}{x_1}= \arctan \frac{3}{4}\hspace{0.15cm}\underline{ = 36.9^{\circ}}.$$

(2)  Multiplying  $z_1$  by its conjugate complex  $z_1^{\star}$  yields the purely real quantity  $z_4$, as the following equations show:

$$z_4 = (x_1 + {\rm j} \cdot y_1)(x_1 - {\rm j} \cdot y_1)= {x_1^2 + y_1^2}= |z_1|^2 = 25,$$

$$z_4 = |z_1| \cdot {\rm e}^{{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm}\phi_1} \cdot |z_1| \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} \phi_1}= |z_1|^2 = 25\hspace{0.3cm} \Rightarrow\hspace{0.3cm} x_4 \hspace{0.1cm}\underline{= 25}, \hspace{0.25cm}y_4 \hspace{0.15cm}\underline{= 0}.$$

(3)  By dividing into real and imaginary part one can write:

$$x_5 = x_1 + 2 \cdot x_2 - {x_3}/{2} = 4 + 2 \cdot(-2) -0 \hspace{0.15cm}\underline{= 0},$$

$$y_5 = y_1 + 2 \cdot y_2 - {y_3}/{2} = 3 + 2 \cdot 0 - \frac{6}{2} \hspace{0.1cm}\underline{=0}.$$

(4)  If one writes  $z_2$  as magnitude and phase  ⇒   $|z_2| = 2, \ \phi_2 = 180^{\circ}$, one obtains for the product:

$$|z_6| = |z_1| \cdot |z_2|= 5 \cdot 2 \hspace{0.15cm}\underline{= 10},$$

$$\phi_6 = \phi_1 + \phi_2 = 36.9^{\circ} + 180^{\circ} = 216.9^{\circ}\hspace{0.15cm}\underline{= -143.1^{\circ}}.$$

(5)  The phase is  $\phi_3 = 90^{\circ}$  (see graph above). This can be formally proven:

$$\phi_3 = \arctan \left( \frac{6}{0}\right) = \arctan (\infty) \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \phi_3 \hspace{0.15cm}\underline{= 90^{ \circ}}.$$

(6)  First, the more inconvenient solution:

$$z_7 = \frac{z_3}{z_1}= \frac{6{\rm j}}{4 + 3{\rm j}} = \frac{6{\rm j}\cdot(4 - 3{\rm j})}{(4 + 3{\rm j})\cdot (4 - 3{\rm j})} = \frac{18 +24{\rm j}}{25} = 1.2 \cdot{\rm e}^{{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 53.1^{ \circ}}.$$

• An easier way of solving the problem is:

$$|z_7| = \frac{|z_3|}{|z_1|} = \frac{6}{5}\hspace{0.15cm}\underline{=1.2}, \hspace{0.3cm}\phi_7 = \phi_3 - \phi_1 = 90^{\circ} - 36.9^{\circ} \hspace{0.15cm}\underline{=53.1^{\circ}}.$$