Exercise 4.3Z: Exponential and Laplace Distribution

• Return to book

WDF von Exponentialverteilung und Laplaceverteilung (unten)

Wir betrachten hier die Wahrscheinlichkeitsdichtefunktionen (WDF) zweier wertkontinuierlicher Zufallsgrößen:

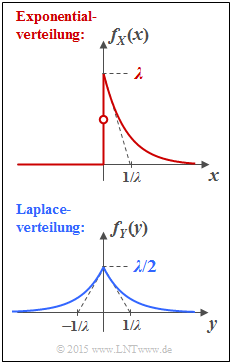
• Die Zufallsgröße  $X$  ist exponentialverteilt (siehe obere Darstellung):   Für  $x<0$  ist  $f_X(x) = 0$,  und für positive $x$–Werte gilt:

$$f_X(x) = \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.05cm}.$$

• Dagegen gilt für die laplaceverteilte Zufallsgröße  $Y$  im gesamten Bereich  $- \infty < y < + \infty$  (untere Skizze):

$$f_Y(y) = \lambda/2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}|\hspace{0.05cm}y\hspace{0.05cm}|}\hspace{0.05cm}.$$

Zu berechnen sind die differentiellen Entropien  $h(X)$  und  $h(Y)$  abhängig vom WDF–Parameter  $\it \lambda$.  Zum Beispiel gilt:

$$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_X)} \hspace{-0.55cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big [f_X(x) \big ] \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$

Bei Verwendung von  $\log_2$  ist die Pseudo–Einheit "bit” anzufügen.

In den Teilaufgaben  (2)  und  (4)  ist die differentielle Entropie in folgender Form anzugeben:

$$h(X) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{{\hspace{-0.01cm} \rm L}}^{\hspace{0.08cm}(X)} \cdot \sigma^2) \hspace{0.5cm}{\rm bzw.} \hspace{0.5cm}h(Y) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{{\hspace{-0.05cm} \rm L}}^{\hspace{0.08cm}(Y)} \cdot \sigma^2) \hspace{0.05cm}.$$

Zu ermitteln ist, durch welchen Faktor  ${\it \Gamma}_{{\hspace{-0.05cm} \rm L}}^{\hspace{0.08cm}(X)}$  die Exponentialverteilung charakterisiert wird und welcher Faktor  ${\it \Gamma}_{{\hspace{-0.01cm} \rm L}}^{\hspace{0.08cm}(Y)}$  sich für die Laplaceverteilung ergibt.

Hinweise:

• Die Aufgabe gehört zum Kapitel  Differentielle Entropie.
• Nützliche Hinweise zur Lösung dieser Aufgabe finden Sie insbesondere auf der Seite  Differentielle Entropie einiger leistungsbegrenzter Zufallsgrößen.
• Für die Varianz der exponentialverteiten Zufallsgröße $X$ gilt, wie in Aufgabe 4.1Z hergeleitet:   $\sigma^2 = 1/\lambda^2$.
• Die Varianz der laplaceverteiten Zufallsgröße $Y$ ist bei gleichem $\it \lambda$ doppelt so groß:   $\sigma^2 = 2/\lambda^2$.

Fragebogen

1

Berechnen Sie die differentielle Entropie der Exponentialverteilung für  $\lambda = 1$.

$h(X) \ = \ $ $\ \rm bit$

2

Welche Kenngröße   ${\it \Gamma}_{{\hspace{-0.01cm} \rm L}}^{\hspace{0.08cm}(X)}$  ergibt sich für die Exponentialverteilung entsprechend der Form  $h(X) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.05cm} \rm L}^{\hspace{0.08cm}(X)} \cdot \sigma^2)$ ?

${\it \Gamma}_{{\hspace{-0.01cm} \rm L}}^{\hspace{0.08cm}(X)} \ = \ $

3

Berechnen Sie die differentielle Entropie der Laplaceverteilung für  $\lambda = 1$.

$h(Y) \ = \ $ $\ \rm bit$

4

Welche Kenngröße  ${\it \Gamma}_{{\hspace{-0.01cm} \rm L}}^{\hspace{0.08cm}(Y)}$  ergibt sich für die Laplaceverteilung entsprechend der Form  $h(Y) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.05cm} \rm L}^{\hspace{0.08cm}(Y)} \cdot \sigma^2)$?

${\it \Gamma}_{{\hspace{-0.01cm} \rm L}}^{\hspace{0.08cm}(Y)} \ = \ $

Musterlösung

Solution

(1)  Obwohl in dieser Aufgabe das Ergebnis in "bit” angegeben werden soll, verwenden wir zur Herleitung den natürlichen Logarithmus.

• Dann gilt für die differentielle Entropie:

$$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm ln} \hspace{0.1cm} \big [f_X(x)\big] \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$

• Für die Exponentialverteilung sind die Integrationsgrenzen  $0$  und  $+∞$  anzusetzen.  In diesem Bereich wird die WDF  $f_X(x)$  gemäß Angabenblatt eingesetzt:

$$h(X) =- \int_{0}^{\infty} \hspace{-0.15cm} \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x} \hspace{0.05cm} \cdot \hspace{0.05cm} \left [ {\rm ln} \hspace{0.1cm} (\lambda) + {\rm ln} \hspace{0.1cm} ({\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x})\right ]\hspace{0.1cm}{\rm d}x - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda) \cdot \int_{0}^{\infty} \hspace{-0.15cm} \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x \hspace{0.1cm} + \hspace{0.1cm} \lambda \cdot \int_{0}^{\infty} \hspace{-0.15cm} \lambda \cdot x \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}x}\hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$

Man erkennt:

• Der erste Integrand ist identisch mit der hier betrachteten WDF  $f_X(x)$.  Das Integral über den gesamten Integrationsbereich ergibt somit  $1$.
• Das zweite Integral entspricht genau der Definition des Mittelwertes  $m_1$  (Moment erster Ordnung).  Für die Exponentialverteilung gilt  $m_1 = 1/λ$.  Daraus folgt:

$$h(X) = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda) + 1 = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda) + \hspace{0.05cm} {\rm ln} \hspace{0.1cm} ({\rm e}) = {\rm ln} \hspace{0.1cm} ({\rm e}/\lambda) \hspace{0.05cm}.$$

• Dieses Ergebnis ist mit der Zusatzeinheit "nat” zu versehen.  Mit  $\log_2$  anstelle von  $\ln$  erhält man die differentielle Entropie in "bit”:

$$h(X) = {\rm log}_2 \hspace{0.1cm} ({\rm e}/\lambda) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda = 1{\rm :} \hspace{0.3cm} h(X) = {\rm log}_2 \hspace{0.1cm} ({\rm e}) = \frac{{\rm ln} \hspace{0.1cm} ({\rm e})}{{\rm ln} \hspace{0.1cm} (2)} \hspace{0.15cm}\underline{= 1.443\,{\rm bit}} \hspace{0.05cm}.$$

(2)  Unter Berücksichtigung der für die Exponentialverteilung gültigen Gleichung  $\sigma^2 = 1/\lambda^2$  kann man das in  (1)  gefundene Ergebnis wie folgt umformen:

$$h(X) = {\rm log}_2 \hspace{0.1cm} ({\rm e}/\lambda) = {1}/{2}\cdot {\rm log}_2 \hspace{0.1cm} ({\rm e}^2/\lambda^2) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ({\rm e}^2 \cdot \sigma^2) \hspace{0.05cm}.$$

• Ein Vergleich mit der geforderten Grundform  $h(X) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.05cm} \rm L}^{\hspace{0.08cm}(X)} \cdot \sigma^2)$  führt zum Ergebnis:

$${\it \Gamma}_{{\hspace{-0.05cm} \rm L}}^{\hspace{0.08cm}(X)} = {\rm e}^2 \hspace{0.15cm}\underline{\approx 7.39} \hspace{0.05cm}.$$

(3)  Bei der Laplaceverteilung unterteilen wir den Integrationsbereich in zwei Teilbereiche:

• $Y$  negativ   ⇒   Anteil  $h_{\rm neg}(Y)$,
• $Y$  positiv   ⇒   Anteil  $h_{\rm pos}(Y)$.

Die gesamte differentielle Entropie ergibt sich unter Berücksichtigung von  $h_{\rm neg}(Y) = h_{\rm pos}(Y)$  zu

$$h(Y) = h_{\rm neg}(Y) + h_{\rm pos}(Y) = 2 \cdot h_{\rm pos}(Y)$$

$$\Rightarrow \hspace{0.3cm} h(Y) = - 2 \cdot \int_{0}^{\infty} \hspace{-0.15cm} \lambda/2 \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y} \hspace{0.05cm} \cdot \hspace{0.05cm} \left [ {\rm ln} \hspace{0.1cm} (\lambda/2) + {\rm ln} \hspace{0.1cm} ({\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y})\right ]\hspace{0.1cm}{\rm d}y = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda/2) \cdot \int_{0}^{\infty} \hspace{-0.15cm} \lambda \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y}\hspace{0.1cm}{\rm d}y \hspace{0.1cm} + \hspace{0.1cm} \lambda \cdot \int_{0}^{\infty} \hspace{-0.15cm} \lambda \cdot y \cdot {\rm e}^{-\lambda \hspace{0.05cm}\cdot \hspace{0.05cm}y}\hspace{0.1cm}{\rm d}y \hspace{0.05cm}.$$

Berücksichtigen wir wiederum, dass das erste Integral den Wert  $1$ ergibt  (WDF–Fläche) und das zweite Integral den Mittelwert  $m_1 = 1/\lambda$  angibt, so erhalten wir:

$$h(Y) = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda/2) + 1 = - \hspace{0.05cm} {\rm ln} \hspace{0.1cm} (\lambda/2) + \hspace{0.05cm} {\rm ln} \hspace{0.1cm} ({\rm e}) = {\rm ln} \hspace{0.1cm} (2{\rm e}/\lambda) \hspace{0.05cm}.$$

• Da das Ergebnis in "bit” gefordert ist, muss noch  $\ln$  durch  $\log_2$  ersetzt werden:

$$h(Y) = {\rm log}_2 \hspace{0.1cm} (2{\rm e}/\lambda) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda = 1{\rm :} \hspace{0.3cm} h(Y) = {\rm log}_2 \hspace{0.1cm} (2{\rm e}) \hspace{0.15cm}\underline{= 2.443\,{\rm bit}} \hspace{0.05cm}.$$

(4)  Bei der Laplaceverteilung gilt der Zusammenhang  $\sigma^2 = 2/\lambda^2$.  Damit erhält man:

$$h(X) = {\rm log}_2 \hspace{0.1cm} (\frac{2{\rm e}}{\lambda}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} (\frac{4{\rm e}^2}{\lambda^2}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} (2 {\rm e}^2 \cdot \sigma^2) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\it \Gamma}_{{\hspace{-0.05cm} \rm L}}^{\hspace{0.08cm}(Y)} = 2 \cdot {\rm e}^2 \hspace{0.15cm}\underline{\approx 14.78} \hspace{0.05cm}.$$

• Der  ${\it \Gamma}_{{\hspace{-0.05cm} \rm L}}$–Wert ist demzufolge bei der Laplaceverteilung doppelt so groß wie bei der Exponentialverteilung.
• Die Laplaceverteilung ist also bezüglich der differentiellen Entropie besser als die Exponentialverteilung, wenn man von leistungsbegrenzten Signalen ausgeht.
• Unter der Nebenbedingung der Spitzenwertbegrenzung sind sowohl die Exponential– als auch die Laplaceverteilung völlig ungeeignet, ebenso wie die Gaußverteilung.  Diese reichen alle bis ins Unendliche.