Exercise 2.11: Arithmetic Coding
Arithmetic coding is a special form of entropy coding: The symbol probabilities must also be known here. In this task, we assume $M = 3$ symbols, which we name with $\rm X$, $\rm Y$ and $\rm Z$ . While Huffman coding is done symbol by symbol, in Arithmetic Coding $(\rm AC)$ a sequence of symbols of length $N$ is coded together. The coding result is a real numerical value $r$ from the interval
- $$I = \big[B, \ E \big) = \big[B, \ B +{\it \Delta} \big)\hspace{0.05cm}.$$
This notation means:
- The beginning $B$ belongs to the interval $I$.
- The end $E$ is no longer contained in $I$ .
- The interval width is ${\it} \Delta = E - B$.
Of the infinite number of possible values $r \in I$ $($since $r$ is real-valued, i.e. not an integer$)$ , the numerical value that gets by with the smallest number of bits is selected. Here are two examples for clarification:
- The deciaml value $r = 3/4$ can be represented with two bits:
- $$r = 1 \cdot 2^{-1} + 1 \cdot 2^{-2} = 0.75 \hspace{0.3cm} \Rightarrow\hspace{0.3cm}\text{binary:}\hspace{0.25cm} 0.11\hspace{0.3cm}\Rightarrow\hspace{0.3cm}\text {Code:} \hspace{0.25cm} \boldsymbol{\rm 11} \hspace{0.05cm}, $$
- The decimal value $r = 1/3$ , on the other hand, requires an infinite number of bits:
- $$r = 0 \cdot 2^{-1} + 1 \cdot 2^{-2} + 1 \cdot 2^{-3}+ 1 \cdot 2^{-4}+ 0 \cdot 2^{-5} + 1 \cdot 2^{-6} + \hspace{0.05cm}\text{...}$$
- $$ \Rightarrow\hspace{0.3cm}\text{binär:} \hspace{0.25cm}0.011101\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \text{Code:} \hspace{0.25cm} \boldsymbol{\rm 011101} \hspace{0.05cm}. $$
In this task we restrict ourselves to the determination of the current interval $I$, marked by the beginning $B$ as well as the end $E$ and the width $\Delta$ respectively.
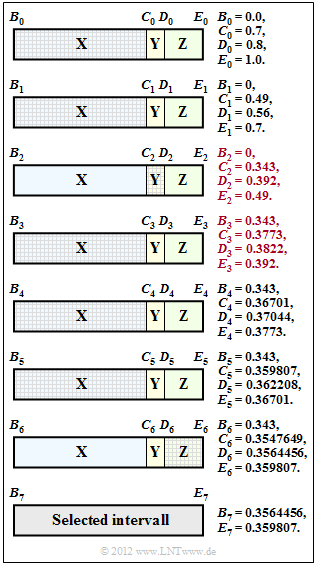
- This determination is done according to the interval nesting in the above diagram.
- The hatching shows that the sequence begins with the ternary symbols $\rm XXY$ .
The algorithm works as follows:
- Before the beginning (quasi at the zero symbol) the entire probability range is divided into three areas according to the probabilities $p_{\rm X}$, $p_{\rm Y}$ and $p_{\rm Z}$ . The limits are
- $$B_0 = 0\hspace{0.05cm},\hspace{0.4cm}C_0 = p_{\rm X}\hspace{0.05cm},\hspace{0.4cm}D_0 = p_{\rm X} + p_{\rm Y}\hspace{0.05cm},\hspace{0.4cm} E_0 = p_{\rm X} + p_{\rm Y}+ p_{\rm Z} = 1\hspace{0.05cm}.$$
- The first symbol of the sequence to be coded is $\rm X$. This means: the selected interval is limited by $B_0$ and $C_0$ . This interval is divided with new beginning $B_1 = B_0$ and new end $E_1 = C_0$ in the same way as the total range in the zero step. The intermediate values are $C_1$ and $D_1$.
- The further interval division is your task. For example, in subtask (2) the boundaries $B_2$, $C_2$, $D_2$ and $E_2$ for the second symbol $\rm X$ are to be determined and in subtask (3) the boundaries $B_3$, $C_3$, $D_3$ and $E_3$ for the third symbol $\rm Y$ are to be determined.
Hints:
- The task belongs to the chapter Other source coding methods.
- In particular, reference is made to the page Arithmetic Coding.
- The binary representation of the selected interval is dealt with in Exercise 2.11Z behandelt.
Questions
Solution
(1) From the graph on the information page you can read the probabilities:
- $$p_{\rm X} = 0.7\hspace{0.05cm},\hspace{0.2cm}p_{\rm Y} = 0.1\hspace{0.05cm},\hspace{0.2cm}p_{\rm Z} = 0.2\hspace{0.05cm}.$$
(2) The second symbol is also $\rm X$. Using the same procedure as in the task description, we get
- $$B_2 \hspace{0.1cm}\underline{= 0}\hspace{0.05cm},\hspace{0.2cm}C_2 = 0.49 \cdot 0.7 \hspace{0.1cm}\underline{= 0.343}\hspace{0.05cm},\hspace{0.2cm} D_2 \hspace{0.1cm} \underline{= 0.392}\hspace{0.05cm},\hspace{0.2cm}E_2 = C_1 \hspace{0.1cm}\underline{= 0.49} \hspace{0.05cm}.$$
(3) For the third symbol $\rm Y$ the limitations $B_3 = C_2$ and $E_3 = D_2$ now apply:
- $$B_3 \hspace{0.1cm}\underline{= 0.343}\hspace{0.05cm},\hspace{0.2cm}C_3 \hspace{0.1cm}\underline{= 0.3773}\hspace{0.05cm},\hspace{0.2cm} D_3 \hspace{0.1cm} \underline{= 0.3822}\hspace{0.05cm},\hspace{0.2cm}E_3 \hspace{0.1cm}\underline{= 0.392} \hspace{0.05cm}.$$
(4) Solution suggestion 1 is correct: From $B_4 = 0.343 = B_3$ (to be read in the diagram on the data sheet) it follows that the fourth source symbol was an $\rm X$ war.
(5) Proposed solutions 2 and 3 are correct:
- The graph shows the interval nesting with all previous results. You can see from the hatching that the second suggested solution gives the correct sequence of symbols: $\rm XXYXXXZ$.
- The interval width $\it \Delta$ can really be determined according to suggestion 3. It holds:
- $${\it \Delta} = 0.359807 - 0.3564456 = 0.003614 \hspace{0.05cm},$$
- $${\it \Delta} =p_{\rm X}^5 \cdot p_{\rm Y} \cdot p_{\rm Z} = 0.7^5 \cdot 0.1 \cdot 0.2 = 0.003614 \hspace{0.05cm}. $$
(6) Correct is the proposed solution 2 ⇒ $r_2 = (0.010111)_{\text{binary}}$, because of:
- $$r_2 = 0 \cdot 2^{-1} + 1 \cdot 2^{-2} + 0 \cdot 2^{-3}+ 1 \cdot 2^{-4}+ 1 \cdot 2^{-5} + 1 \cdot 2^{-6} = 0.359375\hspace{0.05cm}. $$
- Proposition 1: $r_1 = (0.101100)_{\text{binary}}$ must be ruled out because the associated decimal value is $r_1 > 0.5$ .
- The last suggested solution is also wrong, since $r_3 = (0.001011)_{\text{binary}} < (0.01)_{\text{binary}} = (0.25)_{\text{decimal}}$ will be.