Exercise 2.4: Distortion Factor and Distortion Power
A cosine signal
- $$x_1(t) = A_x \cdot \cos(\omega_0 t)$$
with the amplitude $A_x = 1 \ \rm V$ is applied to the input of a message transmission system to test it. Then, the following signal occurs at the system output:
- $$y_1(t) = {0.992 \,\rm V} \cdot \cos(\omega_0 t) - {0.062 \,\rm V} \cdot \cos(2\omega_0 t)+ \hspace{0.05cm}\text{...}$$
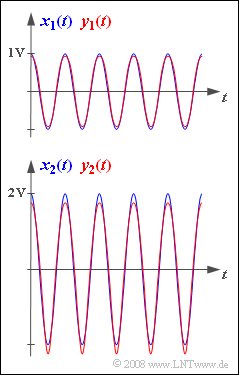
In the upper graph the signals $x_1(t)$ and $y_1(t)$ are shown. Harmonics with amplitudes smaller than $10 \ \rm mV$ are not considered here.
The bottom image shows the input signal $x_2(t)$ with the ampiltude $A_x = 2 \ \rm V$ and the corresponding output signal, again without harmonics smaller than $10 \ \rm mV$:
- $$y_2(t) \hspace{-0.05cm}=\hspace{-0.05cm}{1.938 \,\rm V} \cdot \cos(\omega_0 t)\hspace{-0.05cm} -\hspace{-0.05cm} {0.234 \,\rm V} \cdot \cos(2\omega_0 t) \hspace{-0.05cm}+\hspace{-0.05cm} {0.058 \,\rm V} \cdot \cos(3\omega_0 t)\hspace{-0.05cm} -\hspace{-0.05cm}{0.018 \,\rm V} \cdot \cos(4\omega_0 t) \hspace{-0.05cm}+\hspace{-0.05cm} \hspace{0.05cm}\text{...}$$
It is obvious that the indices "1" and "2" respectively denote the normalised amplitude of the input signal.
The system is supposed to be analysed based on the signal–to–distortion–power ratio
- $$\rho_{\rm V} = { P_{x}}/{P_{\rm V}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} 10 \cdot \lg \hspace{0.1cm}\rho_{\rm V} = 10 \cdot \lg \hspace{0.1cm}{ P_{x}}/{P_{\rm V}}\hspace{0.3cm} \left( {\rm in \hspace{0.15cm} dB} \right)$$
defined in the section Quantitative measure for the signal distortions and the distortion factor $K$ :
- $P_x$ denotes the power of the input signal.
- The distortion power $P_{\rm V}$ respectively represents the power (the root mean square) of the difference signal $\varepsilon(t) = y(t) - x(t)$ .
Zur Bestimmung der Leistungen $P_{x}$ und $P_{\rm V}$ muss jeweils über die quadrierten Signale gemittelt werden. Einfacher ist in dieser Aufgabe jedoch die Leistungsberechnung im Frequenzbereich.
Please note:
- The task belongs to the chapter Nonlinear Distortion.
- All powers required here refer to the resistance $R = 1 \ \rm \Omega$ and thus have the unit ${\rm V}^2$.
Questions
Solution
- $$K \approx K_2 = \frac{0.062 \,\,{\rm V}}{0.992 \,\,{\rm V}} \hspace{0.15cm}\underline{\approx 6.25 \%}.$$
(2) Für die Eingangsamplitude $A_x = 2 \ \rm V$ (untere Skizze) lauten die verschiedenen Klirrfaktoren:
- $$K_2 = \frac{0.234 \,\,{\rm V}}{1.938 \,\,{\rm V}} \approx 0.121, \hspace{0.5cm} K_3 = \frac{0.058 \,\,{\rm V}}{1.938 \,\,{\rm V}} \approx 0.030, \hspace{0.5cm}K_4 = \frac{0.018 \,\,{\rm V}}{1.938 \,\,{\rm V}} \approx 0.009.$$
- Somit lautet der Gesamtklirrfaktor:
- $$K = \sqrt{K_2^2 + K_3^2 + K_4^2 +\text{ ...} }\hspace{0.15cm}\underline{ \approx 12.5 \%}.$$
(3) Richtig sind die beiden ersten Lösungsvorschläge:
- Hier bewirken die nichtlinearen Verzerrungen, dass die untere Halbwelle spitzförmiger verläuft als die obere.
- Da zudem $y(t)$ gleichsignalfrei ist, gilt $y_{\rm max} = 1.75 \ \rm V$ und $y_{\rm min} = -2.25 \ \rm V$. Die Symmetrie bezüglich der Nulllinie ist somit nicht mehr gegeben.
- Bei einem nichtlinearen System ist der Klirrfaktor $K$ unabhängig von der Frequenz des cosinusförmigen Eingangssignals, aber stark abhängig von dessen Amplitude.
(4) Der Effektivwert eines Cosinussignals ist bekanntlich das $\sqrt{0.5}$–fache der Amplitude. Das Quadrat hiervon ergibt die "Leistung":
- $$P_x = \frac{A_x^2}{2} = \frac{(2 \,{\rm V})^2}{2}\hspace{0.15cm}\underline{ = 2\,{\rm V^2}}.$$
- Eigentlich hängt die Leistung ja auch vom Bezugswiderstand $R$ ab und besitzt die Einheit "Watt".
- Mit $R = 1 \ \rm \Omega$ ergibt sich $P_x = 2 \ \rm W$, also der genau gleiche Zahlenwert wie bei dieser einfacheren Berechnung.
(5) Bezeichnet man
- mit $A_1$ die Amplitude der Grundwelle von $y_2(t)$, und
- mit $A_2$, $A_3$ und $A_4$ die so genannten Oberwellen,
so erhält man für die Verzerrungsleistung durch Berechnung im Frequenzbereich:
- $$P_{\rm V} = \frac{1}{2} \cdot \big[ (A_1 - A_x)^2 + A_2^2+ A_3^2+ A_4^2\big] = \frac{1}{2} \cdot \big[ (-2 \,{\rm V} \hspace{-0.05cm}+ \hspace{-0.05cm}1.938 \,{\rm V} )^2 \hspace{-0.05cm}+ \hspace{-0.05cm} (0.234 \,{\rm V})^2 \hspace{-0.05cm}+ \hspace{-0.05cm} (0.058 \,{\rm V})^2 \hspace{-0.05cm}+ \hspace{-0.05cm} (0.018 \,{\rm V})^2 \big] \hspace{0.15cm}\underline{\approx 0.031 \,{\rm V}^2}.$$
Hierbei bezeichnet $A_x$ die Amplitude des Eingangssignals. Die Vorzeichen der Oberwellen spielen bei dieser Berechnung keine Rolle.
(6) Mit den Ergebnissen der Unterpunkte (4) und (5) erhält man:
- $$10 \cdot \lg \rho_{V} = 10 \cdot \lg \frac{P_x}{P_{\rm V}}= 10 \cdot \lg \frac{2.000\,{\rm V^2}}{0.031 \,{\rm V}^2} \hspace{0.15cm}\underline{\approx 18.10 \,{\rm dB}}.$$
(7) Richtig sind die Lösungsvorschläge 1 und 3:
- Die erste Aussage ist richtig, denn es gilt
- $$K^2 = \frac{A_2^2 + A_3^2 + A_4^2 + ... }{A_1^2}.$$
- Dagegen gilt für den Kehrwert des Signal–zu–Verzerrungs–Leistungsverhältnisses:
- $${1}/{\rho_{\rm V}} = \frac{(A_1 - A_x)^2+A_2^2 + A_3^2 + A_4^2 + \text{...} }{A_x^2}.$$
- Bei der Berechnung der Verzerrungsleistung $P_{\rm V}$ wird auch eine Verfälschung der Grundwellenamplitude $($diese ist nun $A_1$ anstelle von $A_x)$ berücksichtigt. Außerdem wird die Verzerrungsleistung nicht auf $A_1^2$, sondern auf $A_x^2$ bezogen.
- Allgemein gilt zwischen dem Signal–zu–Verzerrungs–Leistungsverhältnis und dem Klirrfaktor folgender Zusammenhang:
- $${\rho_{\rm V}} = \frac{A_x^2}{(A_1 - A_x)^2 + K^2 \cdot A_1^2}.$$
- Mit $A_1 = A_x$ vereinfacht sich diese Gleichung wie folgt:
- $${\rho_{\rm V}} = {1}/{ K^2 }.$$
Anmerkungen:
- Ein Klirrfaktor von $1\%$ entspricht in diesem Fall dem Ergebnis $10 \cdot \lg \rho_{\rm V} = 40 \,{\rm dB}$.
- Mit dem Klirrfaktor $K = 0.125$ aus Teilaufgabe (2) hätte man mit der Näherung $A_1 \approx A_x$ sofort $10 \cdot \lg \rho_{\rm V} = 18.06 \,{\rm dB}$ erhalten.
- Der unter Punkt (7) errechnete tatsächliche Wert $(18.10 \ \rm dB)$ weicht hiervon nur unwesentlich ab.