Exercise 3.11: Erasure Channel

Erasure channel with
four inputs and five outputs

An erasure channel is considered with

the $M$ inputs $x ∈ X = \{1,\ 2, \ \text{...} \ ,\ M\}$, and
the $M + 1$ outputs $y ∈ Y = \{1,\ 2,\ \ \text{...} \ ,\ M,\ \text{E}\}.$

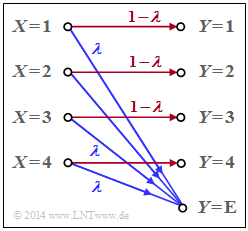
The graph shows the model for the special case $M = 4$. The sink symbol $y = \text{E}$ takes into account an erasure for the case that the receiver cannot make a sufficiently certain decision.

The transition probabilities are given for $1 ≤ μ ≤ M$ as follows:

$${\rm Pr}(Y \hspace{-0.05cm} = \mu\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= \mu) = 1-\lambda \hspace{0.05cm},$$

$${\rm Pr}(Y \hspace{-0.05cm} = {\rm E}\hspace{-0.05cm}\mid \hspace{-0.05cm} X \hspace{-0.05cm}= \mu) = \lambda \hspace{0.05cm}.$$

We are looking for:

the capacity $C_{M\rm –EC}$ of this M–ary Erasure Channel,
the capacity $C_{\rm BEC}$ of the Binary Erasure Channels as a special case of the above model.

Hints:

The exercise belongs to the chapter Application to Digital Signal Transmission.
Reference is made in particular to the page Information-theoretical model of digital signal transmission.
In the above diagram, "erasures" $($with probability $λ)$ are drawn in blue.
"Correct transmission paths" $($i.e., from $X = μ$ to $Y = μ)$ are shown in red ($1 ≤ μ ≤ M$).

Questions

	$P_X(X) = (0.5, \ 0.5),$
	$P_X(X) = (1/M,\ 1/M, \ \text{...} \ ,\ 1/M),$
	$P_X(X) = (0.1,\ 0.2,\ 0.3,\ 0.4).$

	Exactly $M · (M + 1)$,
	Exactly $M$,
	Exactly $2 · M$.

$H(Y) \ = \ $

$\ \rm bit$

$H(Y|X) \ = \ $

$\ \rm bit$

$M = 4\text{:} \hspace{0.5cm} C\ = \ $

$\ \rm bit$

$M = 2\text{:} \hspace{0.5cm} C\ = \ $

$\ \rm bit$

	$C_{\rm BEC} = 1 - λ,$
	$C_{\rm BEC} = 1 - H_{\rm bin}(λ).$

Solution

(1) Correct is the proposed solution 2:

Due to the symmetry of the transition probabilities $P_{Y|X}(Y|X)$ it is obvious that a uniform distribution will lead to the maximum mutual information $I(X; Y)$ and therefore to the channel capacity $C$ :

$$ P_X(X) = P_X\big ( \hspace{0.03cm}X\hspace{-0.03cm}=1\hspace{0.03cm}, \hspace{0.08cm} X\hspace{-0.03cm}=2\hspace{0.03cm},\hspace{0.08cm}\text{...}\hspace{0.08cm}, X\hspace{-0.03cm}=M\hspace{0.03cm}\big ) = \big [\hspace{0.03cm}1/M\hspace{0.03cm}, \hspace{0.08cm} 1/M\hspace{0.03cm},\hspace{0.03cm}\text{...}\hspace{0.08cm},\hspace{0.08cm} 1/M\hspace{0.03cm}\big ]\hspace{0.05cm}.$$

In the special case $M = 2$ also $P_X(X) = (0.5, \ 0.5)$ would be correct.

(2) Correct is the proposed solution 3, i.e. exactly $2M$ connections. Because:

From each source symbol $X = μ$ one gets to the sink symbol $Y = μ$ as well as to the erasure $Y = \text{E}$.

(3) All probabilities ${\rm Pr}(Y = 1), \hspace{0.05cm} \text{...}\hspace{0.05cm} , \hspace{0.08cm}{\rm Pr}(Y = M)$ are equal. Thus, for $μ = 1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \hspace{0.08cm} M$ we obtain:

$${\rm Pr}(Y \hspace{-0.05cm} = \mu) = ( 1-\lambda)/M \hspace{0.05cm}.$$

Moreover, from each source symbol $X = 1, \hspace{0.05cm} \text{...}\hspace{0.05cm} , X = M$ one also gets to the erasure $Y = \text{E}$:

$${\rm Pr}(Y \hspace{-0.05cm} = {\rm E}) = \lambda \hspace{0.05cm}.$$

Inspection reveals that the sum of all $M + 1$ sink symbol probabilities actually adds up t $1$ .
It follows for the sink entropy:

$$H(Y) = M \cdot \frac{ 1-\lambda }{M} \cdot {\rm log}_2 \hspace{0.1cm} \frac{M}{1 - \lambda} \hspace{0.15cm}+\hspace{0.15cm} \lambda \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{\lambda} \hspace{0.05cm}.$$

Summarized with the binary entropy function, this gives:

$$H(Y) = (1-\lambda) \cdot {\rm log}_2 \hspace{0.1cm} M \hspace{0.15cm}+\hspace{0.15cm} H_{\rm bin} (\lambda ) \hspace{0.05cm}$$

and with $M = 4$ as well as $ λ = 0.2$:

$$H(Y) = 1.6 \,{\rm bit} + H_{\rm bin} (0.2 ) \hspace{0.15cm} \underline {=2.322\,{\rm bit}} \hspace{0.05cm}.$$

(4) The $2M$ joint probabilities

$${\rm Pr} \big[(X = μ) ∩ (Y = κ)\big] ≠ 0$$

and the conditional probabilities

$$pκ|μ = {\rm Pr}(Y = κ|X = μ)$$

show the following properties:

The combination $p_{μκ} = (1 – λ)/M$ and $p_{κ|μ} = 1 – λ$ occurs $M$ times.
The combination $p_{μκ} = λ/M$ and $p_{κ|μ} = λ$ also occurs $M$ times.

It follows that:

$$ H(Y \hspace{-0.15cm}\mid \hspace{-0.15cm} X) \hspace{-0.01cm} =\hspace{-0.01cm} M \cdot \frac{ 1-\lambda }{M} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \lambda} \hspace{0.15cm}+\hspace{0.15cm}M \cdot \frac{ \lambda }{M} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ \lambda} = ( 1-\lambda) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1 - \lambda} \hspace{0.15cm}+\hspace{0.15cm} \lambda \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ \lambda} = H_{\rm bin} (\lambda)\hspace{0.05cm}.$$

The result is independent of $M$. With $λ = 0.2$ we obtain:

$$H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H_{\rm bin} (0.2 ) \hspace{0.15cm} \underline {=0.722\,{\rm bit}} \hspace{0.05cm}.$$

(5) The channel capacity $C$ is equal to the maximum mutual information $I(X; Y)$, where the maximization with respect to $P_X(X)$ has already been considered by the symmetric approach:

$$ C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) = H(Y) - H(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = ( 1-\lambda) \cdot {\rm log}_2 \hspace{0.1cm} M + H_{\rm bin} (\lambda) - H_{\rm bin} (\lambda) = ( 1-\lambda) \cdot {\rm log}_2 \hspace{0.1cm} M \hspace{0.05cm}$$

$$\Rightarrow \hspace{0.3cm} M = 4\text{:} \hspace{0.3cm} \underline {C=1.6\,\,{\rm bit}} \hspace{0.05cm}, \hspace{0.8cm} M = 2\text{:} \hspace{0.3cm} \underline {C=0.8\,\,{\rm bit}} \hspace{0.05cm}.$$

(6) The "Binary Erasure Channel" $\rm (BEC)$ is a special case of the general model considered here with $M = 2$:

$$C_{\rm BEC} = 1-\lambda \hspace{0.05cm}.$$

Thus, the correct solution proposal 1.
The second proposed solution, on the other hand, applies to the "Binary Symmetric Channel" $\rm (BSC)$ with distortion probability $λ$.