Exercise 3.15: Data Processing Theorem

"Data Processing Theorem"

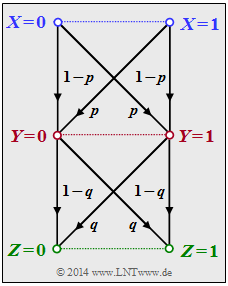
We consider the following data processing chain:

Binary input data $X$ is processed by processor $1$ (top half in the graph) which is describable by conditional probabilities ⇒ $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(\cdot)$ . Its output variable is $Y$.
A second processor with random variable $Y$ at input and random variable $Z$ at output is given by $P_{Z\hspace{0.03cm}|\hspace{0.03cm}Y}(\cdot)$ (lower half in the graph). $Z$ depends on $Y$ alone (deterministic or stochastic) and is independent of $X$:

$$P_{Z\hspace{0.05cm}|\hspace{0.03cm} XY\hspace{-0.03cm}}(z\hspace{0.03cm}|\hspace{0.03cm} x, y) =P_{Z\hspace{0.05cm}|\hspace{0.03cm} Y\hspace{-0.03cm}}(z\hspace{0.03cm}|\hspace{0.03cm} y) \hspace{0.05cm}.$$

The following nomenclature was used for this description:

$$x \in X = \{0, 1\}\hspace{0.02cm},\hspace{0.3cm} y \in Y = \{0,1\}\hspace{0.02cm},\hspace{0.3cm} z \in Z = \{0, 1\}\hspace{0.02cm}.$$

The joint probability mass function is:

$$P_{XYZ}(x, y, z) = P_{X}(x) \cdot P_{Y\hspace{0.05cm}|\hspace{0.03cm} X\hspace{-0.03cm}}(y\hspace{0.03cm}|\hspace{0.03cm} x)\cdot P_{Z\hspace{0.05cm}|\hspace{0.03cm} Y\hspace{-0.03cm}}(z\hspace{0.03cm}|\hspace{0.03cm} y) \hspace{0.05cm}.$$

This also means:

$X → Y → Z$ form a Markov chain. For such a one, the "Data Processing Theorem" holds with the following consequence:

$$I(X;Z) \le I(X;Y ) \hspace{0.05cm}, $$

$$I(X;Z) \le I(Y;Z ) \hspace{0.05cm}.$$

The theorem thus states:

One cannot gain additional information about input $X$ by manipulating ("processing") data $Y$ .
Data processing (by processor $1$) serves only the purpose of making the information contained in $X$ more visible.

Hints:

The task belongs to the chapter Application to Digital Signal Transmission.
Reference is also made to the page Chain rule of the mutual information in the previous chapter]].

Questions

	The derivation is based on the properties of a strictly symmetric channel.
	It is exploited that $H_{\rm bin}(p)$ is a concave function.
	The result is valid for any probability mass function $P_X(X)$.

$ I(X; Y) \ = \ $

$\ \rm bit$

$I(Y; Z) \ = \ $

$\ \rm bit$

$I(X; Z) \ = \ $

$\ \rm bit$

	Yes,
	No.

Solution

(1) Only solution proposal 1 is correct:

Both processors describe strictly symmetric channels ⇒ both uniformly dispersive and uniformly focusing.
For such a binary channel, with $Y = \{0, 1\} \ ⇒ \ |Y| = 2$:

$$I(X;Y) = 1 + \sum_{y \hspace{0.05cm}\in\hspace{0.05cm} Y} \hspace{0.1cm} P_{Y\hspace{0.03cm}|\hspace{0.03cm} X}(y\hspace{0.03cm}|\hspace{0.03cm}x) \cdot {\rm log}_2 \hspace{0.1cm}P_{\hspace{0.01cm}Y \hspace{0.03cm}|\hspace{0.03cm} X}(y\hspace{0.03cm}|\hspace{0.03cm}x) \hspace{0.05cm}.$$

Here it does not matter at all whether one starts from $X = 0$ or from $X = 1$ .
For $X = 0$ one obtains with $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(Y = 1\hspace{0.03cm}|\hspace{0.03cm}X = 0) = p$ and $P_{Y\hspace{0.03cm}|\hspace{0.03cm}X}(Y = 0\hspace{0.03cm}|\hspace{0.03cm}X = 0) = 1 – p\hspace{0.05cm}$:

$$ I(X;Y) = 1 + p \cdot {\rm log}_2 \hspace{0.1cm} (p) + (1-p) \cdot {\rm log}_2 \hspace{0.1cm} (1-p) = 1 - H_{\rm bin}(p)\hspace{0.05cm}, \hspace{1.0cm}H_{\rm bin}(p)= p \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p}+ (1-p) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{1-p}\hspace{0.05cm}.$$

However, the result holds only for $P_X(X) = (0.5, \ 0.5)$ ⇒ maximale mutual information ⇒ channel capacity.
Otherwise, $I(X; Y)$ is smaller. For example, for $P_X(X) = (1, \ 0)$: $H(X) = 0$ ⇒ $I(X; Y) = 0.$
The binary entropy function is concave, but this property was not used in the derivation ⇒ Antwort 2 is incorrect.

(2) For processor $1$ , $p = 0.1\hspace{0.05cm}$ gives:

$$ I(X;Y) = 1 - H_{\rm bin}(0.1) = 1 - 0.469 \hspace{0.15cm} \underline {=0.531 \,{\rm (bit)}} \hspace{0.05cm}.$$

(3) Correspondingly, for the second processor with $q = 0.2\hspace{0.05cm}$:

$$I(Y;Z) = 1 - H_{\rm bin}(0.2) = 1 - 0.722 \hspace{0.15cm} \underline {=0.278 \,{\rm (bit)}} \hspace{0.05cm}.$$

(4) The probability for $Z = 0$ under the condition $X = 0$ results in two ways to

$$P(\hspace{0.01cm}Z\hspace{-0.05cm} = 0\hspace{0.03cm} | \hspace{0.03cm} X\hspace{-0.05cm} = \hspace{-0.05cm}0) = (1-p) \cdot (1-q) + p \cdot q = 1 - p - q + 2pq \stackrel{!}{=} 1 - \varepsilon \hspace{0.05cm}.$$

The overall system then has exactly the same BSC structure as processors $1$ and $2$, but now with falsification probability $\varepsilon = p + q - 2pq \hspace{0.05cm}.$
For $p = 0.1$ and $q = 0.2$ , we obtain:

$$ \varepsilon = 0.1 + 0.2 - 2\cdot 0.1 \cdot 0.2 = 0.26 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) = 1 - H_{\rm bin}(0.26) = 1 - 0.827 \hspace{0.15cm} \underline {=0.173 \,{\rm (bit)}} \hspace{0.05cm}.$$

(5) The answer is YES, of course Data Processing Theorem assumes exactly the conditions given here.

However, we want to evaluate some additional numerical results:

If $0 ≤ p < 0.5$ and $0 ≤ q < 0.5$, hold, we obtain:

$$\varepsilon = p + q \cdot (1-2p) > p \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) < I(X;Y) \hspace{0.05cm},$$

$$\varepsilon = q + p \cdot (1-2q) > q \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) < I(Y;Z) \hspace{0.05cm}.$$

For $p = 0.5$ holds independently of $q$, since $I(X; Z)$ cannot be greater than $I(X; Y)$:

$$\varepsilon = 0.5 + q \cdot (1-1) = 0.5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Y) = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) = 0 \hspace{0.05cm}.$$

Similarly, with $q = 0.5$ independent of $p$, we obtain:

$$\varepsilon = 0.5 + p \cdot (1-1) = 0.5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(Y;Z) = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} I(X;Z) = 0 \hspace{0.05cm}.$$

Also for $p < 0.5$ and $q > 0.5$ the Data Processing Theorem is not violated, which will be shown here only by an example:

With $p = 0.1$ and $q = 0.8$ , the same result is obtained as in subtask (4):

$$\varepsilon = 0.1 + 0.8 - 2\cdot 0.1 \cdot 0.8 = 0.74 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} I(X;Z) = 1 - H_{\rm bin}(0.74) = 1 - H_{\rm bin}(0.26) =0.173 \,{\rm (bit)} \hspace{0.05cm}.$$