Exercise 3.6: Transient Behavior

• Return to book

Cosine and sine waves,
each causal

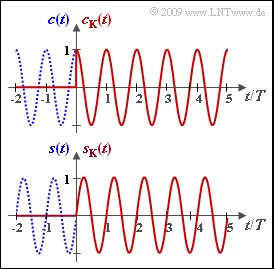
In this exercise, we consider a cosine signal  $c(t)$  with amplitude  $1$  and period $T = 1 \ \rm µ s$, which is defined for all times  $t$  $($in the range  $\pm \infty)$ :

$$c(t) = \cos(2\pi \cdot {t}/{T}) \hspace{0.05cm} .$$

In contrast, the causal cosine signal  $c_{\rm K}(t)$  (red curve) starts only at the turn-on instant  $t = 0$:

$$c_{\rm K}(t)= \left\{ \begin{array}{c} c(t) \\ 0 \end{array} \right. \begin{array}{c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \end{array}\begin{array}{*{20}c} { t \ge 0\hspace{0.05cm},} \\ { t < 0\hspace{0.05cm}.} \end{array}$$

Only the Fourier spectrum can be specified for the bilaterally unbounded signal  $c(t)$ :

$$C(f) = {1}/{ 2} \cdot \delta (f - f_0) + {1}/{ 2} \cdot \delta (f + f_0) \quad {\rm with} \quad f_0 = {1}/{ T}= 1\,\,{\rm MHz.}$$

On the contrary, for the causal cosine signal  $c_{\rm K}(t)$  the Laplace transform can also be specified:

$$C_{\rm L}(p) = \frac {p} { (p-{\rm j} \cdot 2 \pi/T)\cdot (p+{\rm j} \cdot 2 \pi/T)}\hspace{0.05cm} .$$

Accordingly, the following holds for the Laplace transform of the causal sine function  $s_{\rm K}(t)$:

$$S_{\rm L}(p) = \frac {2 \pi/T} { (p-{\rm j} \cdot 2 \pi/T)\cdot (p+{\rm j} \cdot 2 \pi/T)}\hspace{0.05cm} .$$

The bilaterally unbounded sine function is denoted by  $s(t)$  and is shown as a blue–dotted curve in the diagram below.

The signals  $c(t)$,  $c_{\rm K}(t)$,  $s(t)$  and  $s_{\rm K}(t)$  are applied to the input of a low-pass filter of first-order with the following transfer function (or impulse response):

$$H_{\rm L}(p) = \frac {2 /T} { p + 2 /T} \quad \bullet\!\!-\!\!\!-^{\hspace{-0.25cm}\rm L}\!\!\!-\!\!\circ\quad h(t) = {2}/{T} \cdot {\rm e}^{\hspace{0.05cm}-\hspace{0.03cm}2 \hspace{0.03cm}t/T}.$$

• The corresponding output signals are denoted by  $y_{\rm C}(t)$,  $y_{\rm CK}(t)$,  $y_{\rm S}(t)$  and  $y_{\rm SK}(t)$ .
• These signals are to be computed and correlated to each other in this exercise.

Please note:

• The exercise belongs to the chapter  Inverse Laplace Transform.

• The computations for subtask  (6)  are bulky.
• For computing the signals  $y_{\rm CK}(t)$  and  $y_{\rm SK}(t)$,  for example the  residue theorem  can be used.

Questions

1

Compute the frequency response  $H(f)$  using  $H_{\rm L}(p)$  by magnitude and phase.  What values are obtained for frequency  $f = f_0 = 1/T = 1 \ \rm MHz$?

$|H(f = f_0)| \ = \ $

$a(f = f_0)\hspace{0.2cm} = \ $ $\ \rm Np$

${\rm arc} \ H(f = f_0)\ = \ $ $\ \rm Grad$

$b(f = f_0)\hspace{0.24cm} = \ $ $\ \rm Grad$

2

Compute the signal  $y_{\rm C}(t)$  at the filter output if the cosine signal  $c(t)$  is applied to the filter input.  What value is obtained for  $t = 0$?

$y_{\rm C}(t = 0) \ = \ $

3

Compute the output signal  $y_{\rm S}(t)$ if the sine signal  $s(t)$  is applied to the filter input.  What value is obtained for  $t = 0$?

$y_{\rm S}(t = 0) \ = \ $

4

Determine the length of influence  $T_h$  of the filter impulse response, that is the time at which  $h(t)$  has decayed to  $1\%$  of the maximum value. Normalization to  $T$.

$T_h/T \ = \ $

5

Which statements are true for the signals  $y_{\rm CK}(t)$  and  $y_{\rm SK}(t)$ ?

	The following holds:  $y_{\rm CK}(t) \equiv 0$  and  $y_{\rm SK}(t) \equiv 0$  for  $t < 0$.
	The signal  $y_{\rm CK}(t)$  is approximately equal to  $y_{\rm C}(t)$ for  $t > T_h$ .
	The causal signal  $y_{\rm SK}(t)$  is approximately equal to $y_{\rm S}(t)$ for  $t < T_h$ .

6

Using the residue theorem compute the signal  $y_{\rm CK}(t)$  after the filter if  $c_{\rm K}(t)$  is applied to the input.  What signal value occurs at time  $t = T/5$ ?

$y_\text{CK}(t = T/5) \ = \ $

Solution

Solution

(1)  Ersetzt man in  $H_{\rm L}(p)$  den Parameter  $T$  durch  $1/f_0$  sowie  $p$  durch  ${\rm j} \cdot 2 \pi f$, so erhält man für den Frequenzgang allgemein bzw. für  $f_0 = 1 \ \rm MHz$:

$$H(f) = \frac {2 /T} { {\rm j} \cdot 2 \pi f + 2 /T}= \frac {f_0} { {\rm j} \cdot \pi f + f_0} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} H(f= f_0) = \frac {1} { 1 + {\rm j} \cdot \pi }$$

$$\Rightarrow \hspace{0.3cm} |H(f= f_0)| = \frac {1} { \sqrt{1 + \pi^2 }} \hspace{0.15cm}\underline{= 0.303}\hspace{0.05cm},\hspace{0.2cm}a(f= f_0)= - {\rm ln}\,\, |H(f= f_0)| \hspace{0.15cm}\underline{\approx 1.194\,\,{\rm Np}}$$

$$\Rightarrow \hspace{0.3cm} {\rm arc}\,H(f= f_0)= - {\rm arctan}\,(\pi) \hspace{0.15cm}\underline{\approx -72^\circ} \hspace{0.05cm}, \hspace{0.2cm}b(f= f_0)= -{\rm arc}\,H(f= f_0) \hspace{0.15cm}\underline{\approx +72^\circ} \hspace{0.05cm}.$$

(2)  Das Ausgangssignal  $y_{\rm C}(t)$  ist gegenüber dem Eingangssignal  $c(t)$  um den Faktor  $0.303$  gedämpft und um  $\tau \approx 72/360 \cdot T = T/5$  verzögert.

Man kann dieses Signal somit auch folgendermaßen beschreiben:

$$y_{\rm C}(t) = \frac { \cos(2\pi {t}/{T}) + \pi \cdot \sin(2\pi {t}/{T})} { {1 + \pi^2 }}= 0.303 \cdot \cos(2\pi \cdot \frac{t-T/5}{T}) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} y_{\rm C}(t=0) = \frac {1} { {1 + \pi^2 }} \hspace{0.15cm}\underline{\approx 0.092} \hspace{0.05cm}.$$

Dieses Signal ist in der linken Grafik zur Musterlösung  (5)  blau–gepunktet dargestellt.

(3)  Das Signal  $y_{\rm S}(t)$  ist gegenüber  $s(t)$  ebenfalls um den Dämpfungsfaktor  $0.303$  kleiner und um die Zeitdauer  $\tau = T/5$  verzögert.

Es lässt sich wie folgt beschreiben:

$$y_{\rm S}(t) = \frac { -\pi \cdot \cos(2\pi {t}/{T}) + \sin(2\pi {t}/{T})} { {1 + \pi^2 }}= 0.303 \cdot \sin(2\pi \cdot \frac{t-T/5}{T}) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} y_{\rm S}(t=0) = -\frac {\pi} { {1 + \pi^2 }} \hspace{0.15cm}\underline{\approx -0.289} \hspace{0.05cm}.$$

Dieses Signal ist in der rechten Grafik zur Musterlösung  (5)  blau–gepunktet skizziert.

(4)  Bei  $T_h$  soll die Impulsantwort  $h(t)$  auf  $1\%$  des Maximalwertes abgeklungen sein. Somit gilt:

$${\rm e}^{\hspace{0.05cm}-\hspace{0.03cm}2 \hspace{0.03cm}T_{ h}/T} = 0.01 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {T_{ h}}/{T} =\frac{1}{2} \cdot {\rm ln}\,\, \frac{1}{0.01} \hspace{0.15cm}\underline{\approx 2.3} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}h(t=0) = {2}/{T}\hspace{0.05cm}, \hspace{0.2cm}h(t=T_{ h}) = {0.02}/{T}\hspace{0.05cm}.$$

(5)  Richtig sind die Aussagen 1 und 2:

• Die kausalen Signale  $y_{\rm CK}(t)$  und  $y_{\rm SK}(t)$  müssen für  $t < 0$  identisch Null sein.
• Da aber die Impulsantwort  $h(t)$  des betrachteten Filters für  $t > T_h$  (nahezu) verschwindet, ist es nach Abschluss des Einschwingvorganges egal, ob das zeitlich unbegrenzte Cosinussignal  $c(t)$  oder das kausale Signal  $c_{\rm K}(t)$ am Eingang anliegt.
• Das gleiche gilt für die Sinussignale:   Für  $t >T_{ h}$  ist  $y_{\rm SK}(t)=y_{\rm S}(t)$.

Einschwingverhalten eines kausalen Cosinus– und eines kausalen Sinussignals

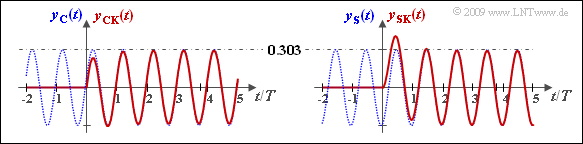
Die Grafik zeigt links die Ausgangssignale  $y_{\rm C}(t)$  und  $y_{\rm CK}(t)$  bei cosinusförmigem Eingang und rechts die Signale  $y_{\rm S}(t)$  und  $y_{\rm SK}(t)$  bei sinusförmigem Eingang. Beachten Sie die Laufzeit von  $T/5$  $($entsprechend der Phase  $72^\circ)$  in beiden Fällen.

• Bei  $y_{\rm CK}(t)$  sind die ersten Wellenberge kleiner als  $1$, um die richtige Phasenlage von  $y_{\rm C}(t)$  zu erreichen.
• Bei  $y_{\rm SK}(t)$  sind dagegen die ersten Wellenberge größer als  $1$, um die richtige Phasenlage von  $y_{\rm S}(t)$  zu erreichen.

(6)  Mit  $p_{\rm x1}= {\rm j} \cdot {2\pi}/{T} , \hspace{0.1cm}p_{\rm x2}= -{\rm j} \cdot {2\pi}/{T} , \hspace{0.1cm} p_{\rm x3}= -{2}/{T} \hspace{0.05cm}$  kann für die Laplace–Transformierte des Signals  $y_{\rm CK}(t)$  geschrieben werden:

$$Y_{\rm L}(p) = \frac {-p_{{\rm x}3}\cdot p} { (p-p_{{\rm x}1})(p-p_{{\rm x}2})(p-p_{{\rm x}3})} \hspace{0.05cm}.$$

Die Zeitfunktion  $y_{\rm CK}(t)$  setzt sich somit nach dem Residuensatz aus drei Anteilen zusammen:

• Der erste Anteil ergibt sich unter Berücksichtigung von  $p_{\rm x2}= -p_{\rm x1}$  zu

$$y_1(t)= {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}} \hspace{0.05cm}\{Y_{\rm L}(p)\cdot {\rm e}^{\hspace{0.03cm}p t}\}= \frac {-p_{{\rm x}3}\cdot p} { (p-p_{{\rm x}2})(p-p_{{\rm x}3})}\cdot {\rm e}^{\hspace{0.03cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}1}}= \frac {-p_{{\rm x}3}\cdot p_{{\rm x}1}} { (p_{{\rm x}1}-p_{{\rm x}2})(p_{{\rm x}1}-p_{{\rm x}3})}\cdot {\rm e}^{\hspace{0.03cm}p_{{\rm x}1}\cdot \hspace{0.03cm}t}= \frac {-p_{{\rm x}3}/2} { p_{{\rm x}1}-p_{{\rm x}3}}\cdot {\rm e}^{\hspace{0.03cm}p_{{\rm x}1}\cdot \hspace{0.03cm}t} \hspace{0.05cm} .$$

• In gleicher Weise erhält man für den zweiten Anteil:

$$y_2(t)= {\rm Res} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}2}} \hspace{0.05cm}\{Y_{\rm L}(p)\cdot {\rm e}^{\hspace{0.03cm}p t}\}= \frac {-p_{{\rm x}3}\cdot p} { (p-p_{{\rm x}1})(p-p_{{\rm x}3})}\cdot {\rm e}^{\hspace{0.03cm}p \hspace{0.05cm}t} \bigg |_{p \hspace{0.05cm}= \hspace{0.05cm}p_{{\rm x}2}}=\frac {-p_{{\rm x}3}\cdot p_{{\rm x}2}} { (p_{{\rm x}2}-p_{{\rm x}1})(p_{{\rm x}2}-p_{{\rm x}3})}\cdot {\rm e}^{\hspace{0.03cm}p_{{\rm x}2}\cdot \hspace{0.03cm}t}= \frac {p_{{\rm x}3}/2} { p_{{\rm x}1}+p_{{\rm x}3}}\cdot {\rm e}^{-p_{{\rm x}1}\cdot \hspace{0.03cm}t} \hspace{0.05cm} .$$

• Fasst man beide Anteile zusammen und berücksichtigt die Zahlenwerte von  $p_{\rm x1}$  und  $p_{\rm x3}$, so erhält man

$$y_{1\hspace{0.03cm}+2}(t)= \frac {1/T} { 2/T + {\rm j} \cdot 2\pi /T} \cdot {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi \hspace{0.03cm} t/T}+\frac {1/T} { 2/T - {\rm j} \cdot 2\pi /T} \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi \hspace{0.03cm}t/T}= \frac {1/2} { 1 + {\rm j} \cdot \pi } \cdot {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi \hspace{0.03cm}t/T}+\frac {1/2} { 1 - {\rm j} \cdot \pi } \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi \hspace{0.03cm}t/T}$$

$$\Rightarrow \hspace{0.3cm} y_{1\hspace{0.03cm}+2}(t)\hspace{0.25cm} = \frac {1/2 \cdot (1 - {\rm j} \cdot \pi)} { 1 + \pi^2 } \cdot {\rm e}^{\hspace{0.03cm}{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi \hspace{0.03cm}t/T}+\frac {1/2 \cdot (1 + {\rm j} \cdot \pi)} { 1 + \pi^2 } \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm}2\pi \hspace{0.03cm}t/T} \hspace{0.05cm} .$$

• Mit Hilfe des Eulerschen Satzes kann hierfür auch geschrieben werden:

$$y_{1\hspace{-0.03cm}+2} (t) = \frac { \cos(2\pi {t}/{T}) + \pi \cdot \sin(2\pi {t}/{T})} { {1 + \pi^2 }}= y_{\rm C}(t)\hspace{0.05cm}.$$

Man erkennt, dass  $y_{1\hspace{0.03cm}+2}(t)$  gleich dem in der Teilaufgabe  (2)  berechneten Signal  $y_{\rm C}(t)$  ist.

• Schließlich erhält man für das letzte Residuum:

$$y_3(t)=\frac {-p_{{\rm x}3}^2} { (p_{{\rm x}3}-p_{{\rm x}1}) (p_{{\rm x}3}-p_{{\rm x}2})} \cdot {\rm e}^{\hspace{0.05cm}p_{{\rm x}3}\cdot \hspace{0.03cm}t}= \frac {-(2/T)^2 \cdot {\rm e}^{\hspace{0.05cm}-2 \hspace{0.03cm}t/T}} { (-2/T-{\rm j} \cdot 2\pi /T) (-2/T+{\rm j} \cdot 2\pi /T)} =\frac {- {\rm e}^{\hspace{0.05cm}-2 \hspace{0.03cm}t/T} } { (1+{\rm j} \cdot \pi ) (1-{\rm j} \cdot \pi)} =\frac {- {\rm e}^{\hspace{0.05cm}-2 \hspace{0.03cm}t/T}} { 1+\pi^2} \hspace{0.05cm} .$$

• Damit lautet das Ausgangssignal bei kausalem Cosinussignal am Eingang:

$$y_{\rm CK}(t) = y_1(t)+y_2(t)+y_3(t) = \frac { \cos(2\pi {t}/{T}) + \pi \cdot \sin(2\pi {t}/{T})-{\rm e}^{\hspace{0.05cm}-2 \hspace{0.03cm}t/T}} { {1 + \pi^2 }}$$

$$\Rightarrow \hspace{0.3cm}y_{\rm CK}(t = {T}/{5}) = \frac { \cos(72^\circ) + \pi \cdot \sin(72^\circ)-{\rm e}^{\hspace{0.05cm}-0.4}} { {1 + \pi^2 }} \hspace{0.15cm}\underline{ \approx 0.24} < 0.303\hspace{0.05cm} .$$

Zum Vergleich:   Das Signal  $y_{\rm C}(t)$  hat zu diesem Zeitpunkt den Wert  $0.303$.

• Dagegen ergibt sich beim kausalen Sinussignal am Eingang allgemein und speziell zum Zeitpunkt des ersten Maximums bei  $t = 0.45 \cdot T$:

$$y_{\rm SK}(t) = \frac { -\pi \cdot \cos(2\pi {t}/{T}) + \sin(2\pi {t}/{T})+\pi \cdot {\rm e}^{\hspace{0.05cm}-2 \hspace{0.03cm}t/T}} { {1 + \pi^2 }}$$

$$\Rightarrow \hspace{0.3cm} y_{\rm SK}(t = 0.45 \cdot T) = \frac { -\pi \cdot \cos(162^\circ) + \sin(162^\circ)+\pi \cdot{\rm e}^{\hspace{0.05cm}-0.9}} { {1 + \pi^2 }} \approx 0.42 > 0.303\hspace{0.05cm} .$$