Exercise 4.Ten: QPSK Channel Capacity

Capacity curves for BPSK and QPSK

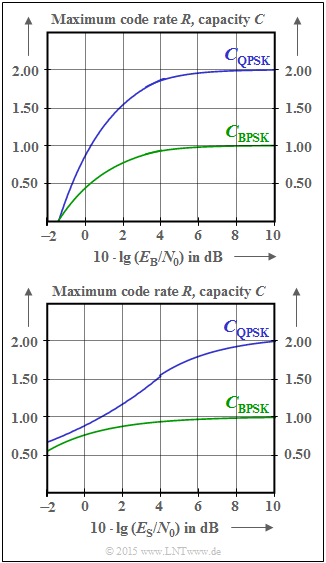
Given are the AWGN channel capacity limit curves for the modulation methods

Binary Phase Shift Keying (BPSK),
Quaternary Phase Shift Keying (4–PSK or QPSK).

The channel capacities $C_\text{BPSK}$ and $C_\text{QPSK}$ simultaneously indicate the maximum code rate $R_{\rm max}$ , with which the bit error probability $p_\text{B} ≡ 0$ can be asymptotically achieved with BPSK (or QPSK) with suitable channel coding.

The upper diagram shows the dependence on the parameter $10 \cdot \lg (E_{\rm B}/{N_0})$ in $\rm dB$, where $E_{\rm B}$ indicates the "energy per information bit".

For large $E_{\rm B}/{N_0}$ values, the BPSK curve provides the maximum code rate $R ≈ 1$.
From the QPSK curve, on the other hand, $R ≈ 2$ can be read.

The capacitance curves for digital input (each with the unit "bit/symbol"),

green curve ⇒ $C_\text{BPSK} (E_{\rm B}/{N_0})$ and
blue curve ⇒ $C_\text{QPSK} (E_{\rm B}/{N_0})$

are to be related in subtask (3) to two Shannon limit curves, each valid for a Gaussian input distribution:

$$C_1( E_{\rm B}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2\cdot R \cdot E_{\rm B}}{N_0}) ,$$

$$C_2( E_{\rm B}/{N_0}) = {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { R \cdot E_{\rm B}}{N_0}) .$$

The two curves simultaneously indicate the maximum code rate $R_{\rm max}$ with which error-free transmission is possible by long channel codes according to the channel coding theorem . Of course, different boundary conditions apply to $C_1( E_{\rm B}/{N_0})$ or $C_2( E_{\rm B}/{N_0})$ . Which ones, you shall find out.

On the other hand, the abscissa in the lower diagram is $10 \cdot \lg (E_{\rm S}/{N_0})$ with the "energy per symbol" $(E_{\rm S})$. Notice that the two limits are not changed from the upper plot::

$$C_{\rm BPSK}( E_{\rm S}/{N_0} \to \infty) = C_{\rm BPSK}( E_{\rm B}/{N_0} \to \infty) = 1 \ \rm bit/symbol,$$

$$C_{\rm QPSK}( E_{\rm S}/{N_0} \to \infty) = C_{\rm QPSK}( E_{\rm B}/{N_0} \to \infty) = 2 \ \rm bit/symbol.$$

Hints:

The task belongs to the chapter AWGN channel capacity with discrete value input.
Reference is made in particular to the page Maximum code rate for QAM structures.

Questions

Solution

QPSK– und 4–QAM–Signalraumkonstellation

(1) The diagram shows the signal space constellations for

Quaternary Phase Shift Keying (QPSK), and
four-level quadrature amplitude modulation (4–QAM).

The latter is also referred to as π/4–QPSK . Both are identical from an information-theoretic point of view ⇒ answer NO.

(2) Correct is the proposed solution 1:

The 4–QAM can be viewed as two BPSK constellations in orthogonal planes, where the energy per information bit $(E_{\rm B})$ is the same in both cases.
Since, according to subtask (1) the 4–QAM is identical to the QSPK, in fact:

$$C_{\rm QPSK}( E_{\rm B}/{N_0}) = 2 \cdot C_{\rm BPSK}( E_{\rm B}/{N_0}).$$

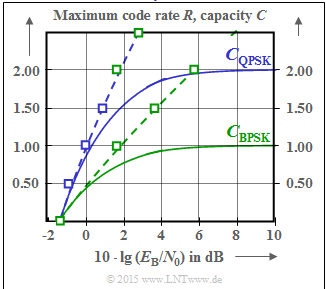
(3) In the lower graph, the two Shannon boundary curves given are sketched together with $C_{\rm BPSK}( E_{\rm B}/{N_0})$ and $C_{\rm QPSK}( E_{\rm B}/{N_0})$ :

$$C_1( E_{\rm B}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot R \cdot E_{\rm B}}{N_0}) ,$$

$$C_2( E_{\rm B}/{N_0}) = {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { R \cdot E_{\rm B}}{N_0}) .$$

Four capacity curves with different statements

One can see from this sketch: Proposed solutions 1, 2 and 4 are correct.

The green–dashed curve $C_1( E_{\rm B}/{N_0})$ is valid for the AWGN channel with Gaussian distributed input.
For code rate $R =1$ , $10 \cdot \lg (E_{\rm B}/{N_0}) = 1.76\ \rm dB$ is required according to this curve.
For $R =2$ , on the other hand $10 \cdot \lg (E_{\rm B}/{N_0}) = 5.74\ \rm dB$ is required.
The blue–dashed curve $C_2( E_{\rm B}/{N_0})$ gives the Shannon limit for $K=2$ parallel Gaussian channels. Here one needs $10 \cdot \lg (E_{\rm B}/{N_0}) = 0\ \rm dB$ for $R =1$ or $10 \cdot \lg (E_{\rm B}/{N_0}) = 1.76\ \rm dB$ for $R =2$.
The one–dimensional BPSK is below $C_1$ in the entire range and thus, of course, below $C_2 > C_1$.
As expected, the two–dimensional QPSK lies below the $C_2$ limit curve relevant for it. However, it is above $C_1$ in the lower range $($up to almost $\text{6 dB)}$ .

(4) The $C_{\rm QPSK}( E_{\rm B}/{N_0})$ curve can also be constructed from $C_{\rm BPSK}( E_{\rm B}/{N_0})$, namely

on the one hand by doubling:

$$C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 2 \cdot C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) ,$$

as well as by a shift of $3\ \rm dB$ to the right:

$$C_{\rm QPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0}) = 2 \cdot C_{\rm BPSK}(10 \cdot {\rm lg} \hspace{0.1cm}E_{\rm S}/{N_0} - 3\,{\rm dB}) .$$

The proposed solution 1 is correct. The second proposal takes into account that with QPSK the energy in one dimension is only $E_{\rm S}/2$.

	By doubling: $C_{\rm QPSK}( E_{\rm B}/{N_0}) = 2 \cdot C_{\rm BPSK}( E_{\rm B}/{N_0})$.
	Additionally by a shift to the right.
	Additionally by a shift to the left.
	$C_{\rm QPSK}( E_{\rm B}/{N_0})$ cannot be constructed from $C_{\rm BPSK}( E_{\rm B}/{N_0})$ .

	$C_{\rm BPSK}( E_{\rm B}/{N_0}) \le C_{\rm 1}( E_{\rm B}/{N_0})$ holds.
	$C_{\rm BPSK}( E_{\rm B}/{N_0}) \le C_{\rm 2}( E_{\rm B}/{N_0})$ holds.
	$C_{\rm QPSK}( E_{\rm B}/{N_0}) \le C_{\rm 1}( E_{\rm B}/{N_0})$ holds.
	$C_{\rm QPSK}( E_{\rm B}/{N_0}) \le C_{\rm 2}( E_{\rm B}/{N_0})$ holds.

	By doubling: $C_{\rm QPSK}( E_{\rm S}/{N_0}) = 2 \cdot C_{\rm BPSK}( E_{\rm S}/{N_0})$ and Additionally by a shift to the right.
	By doubling: $C_{\rm QPSK}( E_{\rm S}/{N_0}) = 2 \cdot C_{\rm BPSK}( E_{\rm S}/{N_0})$ and Additionally by a shift to the left.
	$C_{\rm QPSK}( E_{\rm S}/{N_0})$ cannot be constructed from $C_{\rm BPSK}( E_{\rm S}/{N_0})$ .

	Yes.
	No.