Exercise 1.2Z: Linear Distorting System
The modulator, the channel, and the demodulator of a communication system can be represented by a single linear system with a frequency response of
- $$ H(f) = {\rm si }( \pi \cdot f \cdot \Delta t)$$
The corresponding impulse response is rectangular, symmetrical about $t = 0$ and has height $1/Δt$ and (equivalent) duration $Δt$ :
- $$ h(t) = \left\{ \begin{array}{c} 1/\Delta t \\ 1/(2\Delta t) \\ 0 \\ \end{array} \right. \begin{array}{*{4}c} {\rm{for}} \\ {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.005cm} t\hspace{0.05cm} \right| < \Delta t/2,} \\ {\left| \hspace{0.005cm}t\hspace{0.05cm} \right| = \Delta t/2,} \\ {\left|\hspace{0.005cm} t \hspace{0.05cm} \right| > \Delta t/2.} \\ \end{array}$$
This is a slit low-pass filter, as discussed in the chapter Some Low-Pass Functions in Systems Theory in the book „Linear and Time Invariant Systems”.
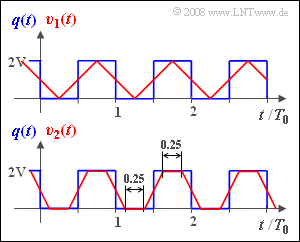
The periodic square wave signal $q(t)$ of period $T_0$ is applied at the system input. Thus, the duration of each rectangle and each gap is $T_0/2$. The height of the rectangles is $2\ \rm V$.
The signal $v(t)$ at the system output is called the sink signal. This is represented in the graph for two different parameter values with equivalent pulse duration (red waveforms):
- The signal $v_1(t)$ results when the equivalent pulse duration of $h(t)$ is exactly $Δt_1$ .
- Accordingly, the signal $v_2(t)$ is obtained with the equivalent pulse duration of $Δt_2$.
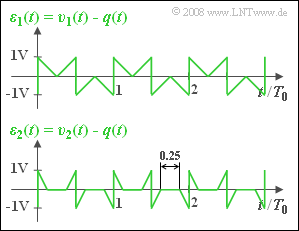
The change from the square wave signal $q(t)$ to the triangular or trapezoidal sink signal $v(t)$ is due to linear distortions and is captured by the error signal $ε(t) = v(t) - q(t)$ .
Using the signal powers $P_q$ and $P_ε$ of $q(t)$ and $ε(t)$ , respectively, the sink SNR can be calculated:
- $$\rho_{v} =P_{q}/{P_{\varepsilon }} \hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter Quality Criteria. Particular reference is made to the page Signal–to–noise (power) ratio and to the chapter Linear Distortions im Buch "Linear and Time Invarian Systems".
- The powers $P_q$ and $P_ε$ are the root mean square values of the signals $q(t)$ and $ε(t)$ and can be determined for periodic signals with period duration $T_0$ as follows:
- $$P_{q} = \overline{q(t)^2} = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} {q(t)^2 }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}, \hspace{0.5cm} P_{\varepsilon} = \overline{\varepsilon(t)^2} = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} {\varepsilon(t)^2 }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$
- Specifying the powers in $\rm V^2$ , means that the signals refer to a resistance of $R = 1\ \rm \Omega$ .
Questions
Solution
- $$\Delta t_1 = T_0 /2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \Delta t_1 / T_0\hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$
(2) Das Fehlersignal $ε_1(t)$ ist in nebenstehender Grafik oben dargestellt. Man erkennt, dass $ε_1(t)$ alle Werte zwischen $±1 \ \rm V$ annehmen kann:
- $${\varepsilon}_\text{ 1, max} \hspace{0.15cm}\underline {= {1}\;{\rm V}} \hspace{0.05cm}.$$
(3) Es genügt die Mittelung über den Zeitbereich von $t = 0$ bis $t =T_0/4$, da alle anderen Teilintervalle genau gleiche Beiträge liefern:
- $$P_{\varepsilon{\rm 1}} = \frac{1}{T_{\rm 0}/4} \hspace{-0.05cm}\cdot \hspace{-0.05cm}\int_{0}^{ T_{\rm 0}/4} {\varepsilon_1(t)^2 }\hspace{0.1cm}{\rm d}t = \frac{1 \,{\rm V}^2}{T_{\rm 0}/4} \hspace{-0.05cm}\cdot \hspace{-0.05cm} \int_{0}^{ T_{\rm 0}/4} {\left( 1 - \frac{t}{T_{\rm 0}/4}\right)^2 }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$
- Mit der Substitution $x = 4 · t/T_0$ kann hierfür auch geschrieben werden:
- $$P_{\varepsilon{\rm 1}} = 1 \,{\rm V}^2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \int_{0}^{ 1} \hspace{-0.2cm}{\left( 1 - 2x + x^2\right)}\hspace{0.1cm}{\rm d}x \hspace{0.05cm}= 1 \,{\rm V}^2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \left( 1 - 1 + \frac{1}{3}\right)\hspace{0.15cm}\underline {= 0.333} \,{\rm V}^2\hspace{0.05cm}.$$
(4) Die Mittelung über eine Periode des quadrierten Quellensignals liefert:
- $$P_{q} = \frac{1}{T_0} \cdot \left[(2\,{\rm V})^2 \cdot \frac{T_0}{2}+(0\,{\rm V})^2 \cdot \frac{T_0}{2} \right]\hspace{0.15cm}\underline {= 2\,{\rm V^2}}\hspace{0.05cm}.$$
- Das Sinken–SNR beträgt somit
- $$\rho_{v{\rm 1}} = \frac{P_{q}}{P_{\varepsilon {\rm 1}}} = \frac{2 \,{\rm V}^2}{0.333 \,{\rm V}^2}\hspace{0.15cm}\underline {= 6} \hspace{0.05cm}.$$
(5) Entsprechend der Skizze auf dem Angabenblatt wird nun aus einem Rechteck der Dauer $0.5 \cdot T_0$ ein Trapez der absoluten Dauer $0.75 · T_0$.
- Damit ist nach den Gesetzen der Faltung offensichtlich, dass die äquivalente Impulsdauer $Δt_2/T_0\hspace{0.15cm}\underline { = 0.25}$ sein muss.
(6) Die untere Skizze in obiger Grafik zeigt, dass sich $ε_2(t)$ ebenso wie $ε_1(t)$ innerhalb einer Periodendauer $T_0$ aus vier Dreiecken zusammensetzt, doch sind diese nur halb so breit.
- In der Hälfte der Zeit ist nämlich $ε_2(t) = 0$.
- Wegen $ε_\text{2, max} = ε_\text{1, max} = 1 \ \rm V$ erhält man:
- $$P_{\varepsilon{\rm 2}} ={P_{\varepsilon{\rm 1}}}/{2} \hspace{0.15cm}\underline {= 0.167} \,{\rm V}^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v{\rm 2}} = {P_{q}}/{P_{\varepsilon {\rm 2}}}\hspace{0.15cm}\underline {= 12} \hspace{0.05cm}.$$
(7) Für $Δt = T_0/2$ wurde in der Teilaufgabe (3) die Verzerrungsleistung $P_{ε1} = 1/3 \ \rm V^{ 2 }$ berechnet.
- In der Teilaufgabe (6) wurde gezeigt, dass bei $Δt = T_0/4$ die Verzerrungsleistung $P_{ε2}$ nur halb so groß ist.
- Anschaulich wurde erläutert, dass ein linearer Zusammenhang besteht. Daraus folgen für $Δt ≤ T_0/2$ die empirischen Gleichungen:
- $$P_{\varepsilon} = \frac{2 \,{\rm V}^2}{3} \cdot \frac{\Delta t}{T_0} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v} = \frac{P_{q}}{P_{\varepsilon }}= \frac{3}{\Delta t/T_0} \hspace{0.05cm}.$$
- Der Sonderfall $Δt = T_0/20$ führt somit zu den Resultaten:
- $$P_{\varepsilon{\rm 3}} = \frac{2 \,{\rm V}^2}{60} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v{\rm 3}} = \frac{P_{q}}{P_{\varepsilon {\rm 3}}}\hspace{0.15cm}\underline {= 60} \hspace{0.05cm}.$$