Exercise 1.2Z: Linear Distorting System
The modulator, the channel, and the demodulator of a communication system can be represented by a single linear system with a frequency response of
- $$ H(f) = {\rm si }( \pi \cdot f \cdot \Delta t)$$
The corresponding impulse response is rectangular, symmetrical about $t = 0$ and has height $1/Δt$ and (equivalent) duration $Δt$ :
- $$ h(t) = \left\{ \begin{array}{c} 1/\Delta t \\ 1/(2\Delta t) \\ 0 \\ \end{array} \right. \begin{array}{*{4}c} {\rm{for}} \\ {\rm{for}} \\ {\rm{for}} \\ \end{array}\begin{array}{*{20}c} {\left| \hspace{0.005cm} t\hspace{0.05cm} \right| < \Delta t/2,} \\ {\left| \hspace{0.005cm}t\hspace{0.05cm} \right| = \Delta t/2,} \\ {\left|\hspace{0.005cm} t \hspace{0.05cm} \right| > \Delta t/2.} \\ \end{array}$$
This is a slit low-pass filter, as discussed in the chapter Some Low-Pass Functions in Systems Theory in the book „Linear and Time Invariant Systems”.
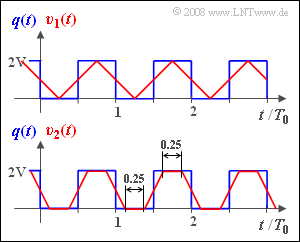
The periodic square wave signal $q(t)$ of period $T_0$ is applied at the system input. Thus, the duration of each rectangle and each gap is $T_0/2$. The height of the rectangles is $2\ \rm V$.
The signal $v(t)$ at the system output is called the sink signal. This is represented in the graph for two different parameter values with equivalent pulse duration (red waveforms):
- The signal $v_1(t)$ results when the equivalent pulse duration of $h(t)$ is exactly $Δt_1$ .
- Accordingly, the signal $v_2(t)$ is obtained with the equivalent pulse duration of $Δt_2$.
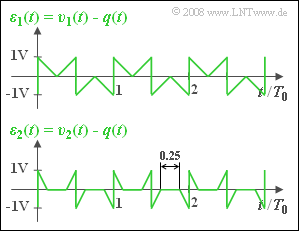
The change from the square wave signal $q(t)$ to the triangular or trapezoidal sink signal $v(t)$ is due to linear distortions and is captured by the error signal $ε(t) = v(t) - q(t)$ .
Using the signal powers $P_q$ and $P_ε$ of $q(t)$ and $ε(t)$ , respectively, the sink SNR can be calculated:
- $$\rho_{v} =P_{q}/{P_{\varepsilon }} \hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter Quality Criteria. Particular reference is made to the page Signal–to–noise (power) ratio and to the chapter Linear Distortions im Buch "Linear and Time Invarian Systems".
- The powers $P_q$ and $P_ε$ are the root mean square values of the signals $q(t)$ and $ε(t)$ and can be determined for periodic signals with period duration $T_0$ as follows:
- $$P_{q} = \overline{q(t)^2} = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} {q(t)^2 }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}, \hspace{0.5cm} P_{\varepsilon} = \overline{\varepsilon(t)^2} = \frac{1}{T_{\rm 0}} \cdot \int_{0}^{ T_{\rm 0}} {\varepsilon(t)^2 }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$
- Specifying the powers in $\rm V^2$ , means that the signals refer to a resistance of $R = 1\ \rm \Omega$ .
Questions
Solution
- $$\Delta t_1 = T_0 /2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \Delta t_1 / T_0\hspace{0.15cm}\underline {= 0.5} \hspace{0.05cm}.$$
(2) The error signal $ε_1(t)$ is shown in the adjacent graph. It can be seen that $ε_1(t)$ can assume all values in the range $±1 \ \rm V$ :
- $${\varepsilon}_\text{ 1, max} \hspace{0.15cm}\underline {= {1}\;{\rm V}} \hspace{0.05cm}.$$
(3) It is sufficient to average over the time range from $t = 0$ to $t =T_0/4$, since all other subintervals contribute identically:
- $$P_{\varepsilon{\rm 1}} = \frac{1}{T_{\rm 0}/4} \hspace{-0.05cm}\cdot \hspace{-0.05cm}\int_{0}^{ T_{\rm 0}/4} {\varepsilon_1(t)^2 }\hspace{0.1cm}{\rm d}t = \frac{1 \,{\rm V}^2}{T_{\rm 0}/4} \hspace{-0.05cm}\cdot \hspace{-0.05cm} \int_{0}^{ T_{\rm 0}/4} {\left( 1 - \frac{t}{T_{\rm 0}/4}\right)^2 }\hspace{0.1cm}{\rm d}t \hspace{0.05cm}.$$
- Substituting $x = 4 · t/T_0$ , this can also be written as:
- $$P_{\varepsilon{\rm 1}} = 1 \,{\rm V}^2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \int_{0}^{ 1} \hspace{-0.2cm}{\left( 1 - 2x + x^2\right)}\hspace{0.1cm}{\rm d}x \hspace{0.05cm}= 1 \,{\rm V}^2 \hspace{-0.05cm}\cdot \hspace{-0.05cm} \left( 1 - 1 + \frac{1}{3}\right)\hspace{0.15cm}\underline {= 0.333} \,{\rm V}^2\hspace{0.05cm}.$$
(4) Averaging over one period of the squared source signal yields:
- $$P_{q} = \frac{1}{T_0} \cdot \left[(2\,{\rm V})^2 \cdot \frac{T_0}{2}+(0\,{\rm V})^2 \cdot \frac{T_0}{2} \right]\hspace{0.15cm}\underline {= 2\,{\rm V^2}}\hspace{0.05cm}.$$
- The sink SNR is therefore
- $$\rho_{v{\rm 1}} = \frac{P_{q}}{P_{\varepsilon {\rm 1}}} = \frac{2 \,{\rm V}^2}{0.333 \,{\rm V}^2}\hspace{0.15cm}\underline {= 6} \hspace{0.05cm}.$$
(5) According to the sketch presented above, a rectangle of duration $0.5 \cdot T_0$ now becomes a trapezoid of absolute duration $0.75 · T_0$.
- Thus, according to the laws of convolution, it is obvious that the equivalent pulse duration must be $Δt_2/T_0\hspace{0.15cm}\underline { = 0.25}$ .
(6) The lower plot in the above graph shows that $ε_2(t)$ is composed of four triangles within a period of $T_0$ just like $ε_1(t)$ , though they are only half as wide.
- Thus, in half the time, $ε_2(t) = 0$.
- Because of $ε_\text{2, max} = ε_\text{1, max} = 1 \ \rm V$ , one obtains:
- $$P_{\varepsilon{\rm 2}} ={P_{\varepsilon{\rm 1}}}/{2} \hspace{0.15cm}\underline {= 0.167} \,{\rm V}^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v{\rm 2}} = {P_{q}}/{P_{\varepsilon {\rm 2}}}\hspace{0.15cm}\underline {= 12} \hspace{0.05cm}.$$
(7) For $Δt = T_0/2$ the distortion power $P_{ε1} = 1/3 \ \rm V^{ 2 }$ was calculated in subtask (3) .
- In subtask (6) it was shown, that for $Δt = T_0/4$ the distortion power $P_{ε2}$ is only half.
- It was clearly illustrated that a linear relationship holds. For $Δt ≤ T_0/2$ we get the following empirical equations:
- $$P_{\varepsilon} = \frac{2 \,{\rm V}^2}{3} \cdot \frac{\Delta t}{T_0} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v} = \frac{P_{q}}{P_{\varepsilon }}= \frac{3}{\Delta t/T_0} \hspace{0.05cm}.$$
- Thus, the special case $Δt = T_0/20$ results in:
- $$P_{\varepsilon{\rm 3}} = \frac{2 \,{\rm V}^2}{60} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v{\rm 3}} = \frac{P_{q}}{P_{\varepsilon {\rm 3}}}\hspace{0.15cm}\underline {= 60} \hspace{0.05cm}.$$