Exercise 2.4Z: Low-pass Influence with Synchronous Demodulation

• Return to book

Signals for DSB–AM and synchronous demodulation

Let us consider the same communication system as in  Exercise 2.4.  But this time, we will assume perfect frequency and phase synchronization for the synchronous demodulator $\rm (SD)$ .

The source signal  $q(t)$,  the transmitted signal  $s(t)$  and the signal  $b(t)$  in the synchronous demodulator before the low-pass filter are given as follows:

$$q(t) = q_1(t) + q_2(t)\hspace{0.2cm}{\rm with }$$

$$q_1(t) = 2\,{\rm V} \cdot \cos(2 \pi \cdot 2\,{\rm kHz} \cdot t)\hspace{0.05cm},$$

$$q_2(t) = 1\,{\rm V} \cdot \sin(2 \pi \cdot 5\,{\rm kHz} \cdot t)\hspace{0.05cm},$$

$$s(t) = q(t) \cdot \sin(2 \pi \cdot 50\,{\rm kHz} \cdot t)\hspace{0.05cm},$$

$$b(t) = s(t) \cdot 2 \cdot \sin(2 \pi \cdot 50\,{\rm kHz} \cdot t)\hspace{0.05cm}.$$

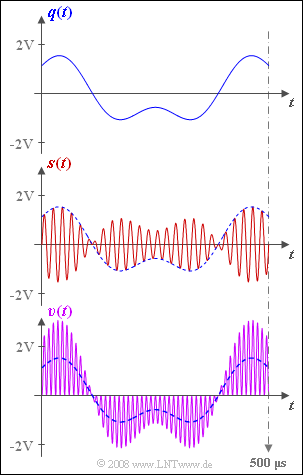
The graph shows the source signal  $q(t)$  at the top and the transmission signal  $s(t)$  in the middle.

The sink signal  $v(t)$  is shown at the bottom (violet waveform).

• This obviously does not match the source signal (blue dashed curve).
• The reason for this undesired result  $v(t) ≠ q(t)$  could be a missing or wrongly dimensioned low-pass filter.

In the subtasks  (3)  and  (4) , a  "trapezoidal low-pass filter"  is used,  whose frequency response is as follows:

$$H_{\rm E}(f) = \left\{ \begin{array}{l} \hspace{0.25cm}1 \\ \frac{f_2 -|f|}{f_2 -f_1} \\ \hspace{0.25cm} 0 \\ \end{array} \right.\quad \quad \begin{array}{*{10}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}c} {\hspace{0.94cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < f_1,} \\ {f_1 \le \left| \hspace{0.005cm}f\hspace{0.05cm} \right| \le f_2,} \\ {\hspace{0.94cm}\left|\hspace{0.005cm} f \hspace{0.05cm} \right| > f_2.} \\ \end{array}$$

Hints:

• This exercise belongs to the chapter   Synchronous Demodulation.
• Particular reference is made to the page   Block diagram and time domain representation.
• In contrast to  Exercise 2.4 ,  $f_1$  and  $f_2$  do not describe signal frequencies, but instead relate to the low-pass filter.

Questions

1

What statements can be made about the  $H_{\rm E}(f)$  filter used to obtain the sink signal shown on the page?

	The upper cutoff frequency is too high.
	The upper cutoff frequency is too low.
	The lower cutoff frequency is not zero.

2

With which of the low-pass functions listed below is ideal demodulation - that is,   $v(t) = q(t)$  – possible in principle?

	Rectangular-in-frequency low-pass,
	Gaussian low-pass,
	trapezoidal low-pass,
	slit low-pass.

3

What is the minimum lower corner frequency  $f_1$  of a trapezoidal low-pass filter one can choose to avoid distortion?

$f_{\text{1, min}} \ = \ $ $\ \text{kHz}$

4

What is the maximum upper corner frequency  $f_2$  of the trapezoidal low-pass that avoids distortion?

$f_{\text{2, max}} \ = \ $ $\ \text{kHz}$

5

Which cutoff frequency  (German:  "Grenzfrequenz"   ⇒   subscript "G")  $f_{\rm G}$  of an ideal rectangular low-pass filter would you choose if distortion is not negligible?

	$f_{\rm G} = 4 \ \rm kHz$,
	$f_{\rm G} = 6 \ \rm kHz$,
	$f_{\rm G} = 10 \ \rm kHz$.

Solution

Solution

(1)  The first statement  is correct:

• The sink signal  $v(t)$  shown in the bottom graphic exactly matches the signal   $b(t)$  given in the equation and thus also contains components around twice the carrier frequency.
• The filter   $H_{\rm E}(f)$  is either missing completely or its upper cutoff frequency  $f_2$  is too high.
• Regarding the lower cutoff frequency   $f_1$,  the only statement possible is that it is smaller than the smallest frequency   $\text{(2 kHz)}$ occurring in the signal  $b(t)$.
• Whether or not a DC component is removed by the filter is unclear,  since such a component is not present in the signal   $b(t)$.

(2)  Answers 1 and 3  are correct:

• A prerequisite for distortion-free demodulation is that all spectral components up to a certain frequency   $f_1$  are transmitted equally and as unattenuated as possible,  and all components at frequencies   $f > f_2$  are completely suppressed.
• The rectangular and trapezoidal low-pass filters satisfy this condition.

(3)  It must be ensured that the  $\text{5 kHz}$  component still lies in the passband:

$$f_{\text{1, min}}\hspace{0.15cm}\underline{ =5 \ \rm kHz}.$$

(4)  All spectral components in the vicinity of twice the carrier frequency – more precisely between  $\text{95 kHz}$  and  $\text{ 105 kHz}$  – must be completely suppressed:

$$f_{\text{2, max}}\hspace{0.15cm}\underline{ =95 \ \rm kHz}.$$

• Otherwise nonlinear distortion would arise.

(5)  Answer 2  is correct:

• The cutoff frequency}  $f_{\rm G} = \text{ 4 kHz}$  would result in  (linear)  distortions,  since the  $\text{5 kHz}$  component would be cut off.
• The low-pass with cutoff frequency  $f_{\rm G} = \text{6 kHz}$  is preferable,  since with  $f_{\rm G} = \text{10 kHz}$  more noise components would be superimposed on the signal  $v(t)$.