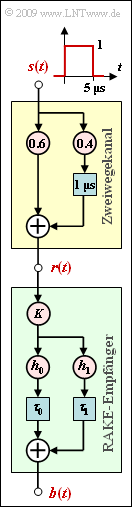
Exercise 5.5Z: About the Rake Receiver
The diagram shows a two-way channel (yellow background). The corresponding descriptive equation is:
- $$ r(t) =0.6 \cdot s(t) + 0.4 \cdot s (t - \tau) \hspace{0.05cm}.$$
Let the delay on the secondary path be $τ = 1 \ \rm µ s$. Drawn below is the structure of a rake receiver (green background) with general coefficients $K$, $h_0$, $h_1$, $τ_0$ and $τ_1$.
The purpose of the rake receiver is to combine the energy of the two signal paths, making the decision more reliable.
The combined impulse response of the channel and the rake receiver can be expressed in the form
- $$h_{\rm KR}(t) = A_0 \cdot \delta (t ) + A_1 \cdot \delta (t - \tau) + A_2 \cdot \delta (t - 2\tau)$$
but only if the rake coefficients $h_0$, $h_1$, $τ_0$ and $τ_1$ are appropriately chosen. The main part of $h_{\rm KR}(t)$ is supposed to be at $t = τ$.
The constant $K$ is to be chosen so that the amplitude of the main path $A_1 = 1$ :
- $$K= \frac{1}{h_0^2 + h_1^2}.$$
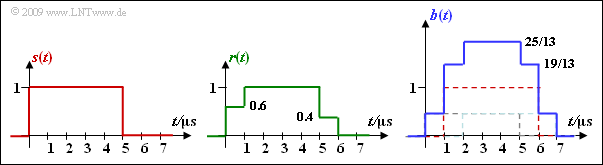
Apart from the rake parameters, the signals $r(t)$ and $b(t)$ are sought when $s(t)$ is a rectangle of height $s_0 = 1$ and width $T = \ \rm 5 µ s$.
Notes:
- The exercise belongs to the chapter Error Probability of Direct-Sequence Spread Spectrum Modulation.
- Reference is made in particular to the section Principle of the rake receiver.
Questions
Solution
- The impulse response $h_{\rm K}(t)$ is obtained as the received signal $r(t)$ when there is a dirac pulse at the input ⇒ $s(t) = δ(t)$. It follows that:
- $$ h_(t) = 0.6 \cdot \delta (t ) + 0.4 \cdot \delta (t - \tau) \hspace{0.05cm}.$$
(2) Solutions 2 and 3 are correct:
- By definition, the channel frequency response $H_{\rm K}(f)$ is the Fourier transform of the impulse response $h_{\rm K}(t)$. With the shift theorem this results in:
- $$H_{\rm K}(f) = 0.6 + 0.4 \cdot {\rm e}^{ \hspace{0.03cm}{\rm j} \hspace{0.03cm} \cdot \hspace{0.03cm}2 \pi f \tau}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} H_{\rm K}(f= 0) = 0.6 + 0.4 = 1 \hspace{0.05cm}.$$
- Accordingly, the first proposed solution is incorrect in contrast to the other two: $H_{\rm K}(f)$ is complex-valued and the magnitude is periodic with $1/τ$, as the following calculation shows:
- $$|H_{\rm K}(f)|^2 = \left [0.6 + 0.4 \cdot \cos(2 \pi f \tau) \right ]^2 + \left [ 0.4 \cdot \sin(2 \pi f \tau) \right ]^2 = \left [0.6^2 + 0.4^2 \cdot \left ( \cos^2(2 \pi f \tau) + \sin^2(2 \pi f \tau)\right ) \right ] + 2 \cdot 0.6 \cdot 0.4 \cdot \cos(2 \pi f \tau)$$
- For $f = 0$, $|H_{\rm K}(f)| = 1$. This value is repeated in the respective frequency spacing $1/τ$.
(3) We first set $K = 1$ as agreed.
- Altogether we get from $s(t)$ to the output signal $b(t)$ via four paths.
- To satisfy the given $h_{\rm KR}(t)$ equation, either $τ_0 = 0$ must hold or $τ_1 = 0$. With $τ_0 = 0$ we obtain for the impulse response:
- $$h_{\rm KR}(t) = 0.6 \cdot h_0 \cdot \delta (t ) + 0.4 \cdot h_0 \cdot \delta (t - \tau) + 0.6 \cdot h_1 \cdot \delta (t -\tau_1) + 0.4 \cdot h_1 \cdot \delta (t - \tau-\tau_1) \hspace{0.05cm}.$$
- To be able to focus the "main energy" on a time point, $τ_1 = τ$ would then have to be chosen. With $h_0 = 0.6$ and $h_1 = 0.4$, we then obtain $A_0 ≠ A_2$:
- $$h_{\rm KR}(t) = 0.36 \cdot \delta (t ) +0.48 \cdot \delta (t - \tau) + 0.16 \cdot \delta (t - 2\tau)\hspace{0.05cm}.$$
- In contrast, with $h_0 = 0.6$, $h_1 = 0.4$, $τ_0 = τ$ and $τ_1 = 0$:
- $$h_{\rm KR}(t) = 0.6 \cdot h_0 \cdot \delta (t - \tau ) + 0.4 \cdot h_0 \cdot \delta (t - 2\tau) + 0.6 \cdot h_1 \cdot \delta (t) + 0.4 \cdot h_1 \cdot \delta (t - \tau)= 0.24 \cdot \delta (t ) +0.52 \cdot \delta (t - \tau) + 0.24 \cdot \delta (t - 2\tau) \hspace{0.05cm}.$$
- Here, the additional condition $A_0 = A_2$ is satisfied. Thus, the result we are looking for is:
- $$ \underline{\tau_0 = \tau = 1\,{\rm µ s} \hspace{0.05cm},\hspace{0.2cm}\tau_1 =0} \hspace{0.05cm}.$$
(4) The following must apply to the normalization factor:
- $$K= \frac{1}{h_0^2 + h_1^2} = \frac{1}{0.6^2 + 0.4^2} = \frac{1}{0.52} \hspace{0.15cm}\underline {\approx 1.923} \hspace{0.05cm}.$$
- This gives for the common impulse response $($it holds $0.24/0.52 = 6/13)$:
- $$ h_{\rm KR}(t) = \frac{6}{13} \cdot \delta (t ) + 1.00 \cdot \delta (t - \tau) + \frac{6}{13} \cdot \delta (t - 2\tau)\hspace{0.05cm}.$$
(5) Statements 1 and 4 are correct, as shown in the diagram:
- For the received signal $r(t)$ and for the rake output signal $b(t)$ holds:
- $$r(t) = 0.6 \cdot s(t) + 0.4 \cdot s (t - 1\,{\rm µ s})\hspace{0.05cm},$$
- $$b(t) = \frac{6}{13} \cdot s(t) + 1 \cdot s (t - 1\,{\rm µ s}) + \frac{6}{13} \cdot s (t - 2\,{\rm µ s}) \hspace{0.05cm}.$$
- The overshoot of the output signal ⇒ $b(t) > 1$ is due to the normalization factor $K = 25/13$.
- With $K = 1$, the maximum value of $b(t)$ would actually be $1$.