Exercise 5.4Z: OVSF Codes

From LNTwww
Revision as of 17:16, 13 December 2021 by Guenter (talk | contribs)

Construction of an OVSF code

The spreading codes for  UMTS  should

  • all be orthogonal to each other in order to avoid mutual interference between subscribers,
  • additionally allow a flexible realization of different spreading factors  J. 


One example of this is the so-called  "Orthogonal Variable Spreading Factor" code,  which provide spreading codes with lengths from  J=4  to  J=512. 

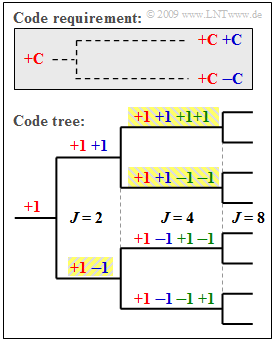
These can be created using a code tree,  as shown in the diagram.  In this process,  two new codes  (+C +C)  and  (+C −C)  are created from a code  C  at each branching.

The diagram illustrates the principle given here with the example  J=4: 

  • If the spreading sequences are numbered from  0  to  J−1  the spreading sequences are as follows
⟨c(0)ν⟩=+1+1+1+1,⟨c(1)ν⟩=+1+1−1−1,
⟨c(2)ν⟩=+1−1+1−1,⟨c(3)ν⟩=+1−1−1+1.
  • According to this nomenclature,  for the spreading factor  J=8  there are the spreading sequences  ⟨c(0)ν⟩,  ... ,  ⟨c(7)ν⟩.
  • Note that no predecessor and successor of a code may be used for another participant.
  • So,  in the example,  four spreading codes with spreading factor  J=4  could be used or the three codes highlighted in yellow – once with  J=2  and twice with  J=4.




Notes:


Questions

1

Construct the tree diagram for  J=8.  What are the resulting OVSF codes?

Codeword 1:   ⟨c(1)ν⟩=+1+1+1+1−1−1−1−1,
Codeword 3:   ⟨c(3)ν⟩=+1+1−1−1+1+1−1−1 ,
Codeword 5:   ⟨c(5)ν⟩=+1−1+1−1+1−1+1−1,
Codeword 7:   ⟨c(7)ν⟩=+1−1−1+1−1+1+1−1.

2

What is the maximum number of UMTS subscribers  (Kmax)  that can be served with  J=8 ?

Kmax = 

3

How many subscribers  (K)  can be served if three of these subscribers are to use a spreading code with  J=4 ?

K = 

4

Assume a tree structure for  J=32.   Is the following assignment feasible:
Twice  J=4,  once  J=8,  twice  J=16  and eight times  J=32?

Yes.
No.


Solution

Solution

OVSF Tree Structure for  J=8

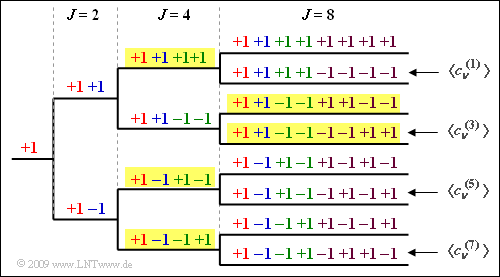
(1)  The diagram shows the OVSF tree structure for  J=8 users.  From this it can be seen that solutions 1, 3 and 4 apply, but not the second one.


(2)  If each user is assigned a spreading code with  J=8,   Kmax=8_  subscribers can be served.


(3)  When three subscribers are served by  J=4  only two subscribers can still be served by a spreading sequence with  J=8  (see exemplary yellow background in the diagram above)   ⇒   K=5_.


(4)  We denote by

  • K4=2  the number of spreading sequences with  J=4,
  • K8=1  the number of spreading sequences with  J=8,
  • K16=2  the number of spreading sequences with  J=16,
  • K32=8  the number of spreading sequences with  J=32.


Then the following condition must be satisfied:

K4⋅324+K8⋅328+K16⋅3216+K32⋅3232≤32⇒K4⋅8+K8⋅4+K16⋅2+K32⋅1≤32.
  • Because of  2·8+1·4+2·2+8=32,  the desired occupancy is just allowed   ⇒   answer YES.
  • For example, supplying the spreading factor  J=4  twice blocks the upper half of the tree.
  • After providing one spreading  J=8, three of the eight branches remain to be occupied on the  J=8 level, and so on.

Retrieved from "http://en.lntwww.de/index.php?title=Aufgaben:Exercise_5.4Z:_OVSF_Codes&oldid=43818"
  • Powered by MediaWiki