Exercise 2.9: Symmetrical Distortions

Transmitter and receiver spectrum in the equivalent low-pass region

The source signal made up of two components

$$q(t) = A_1 \cdot \cos(2 \pi f_1 t ) + A_2 \cdot \cos(2 \pi f_2 t )$$

is amplitude modulated and transmitted through a linearly distorting transmission channel. The carrier frequency is $f_{\rm T}$ and the added DC component $A_{\rm T}$. Thus, a Double-sideband amplitude moduluation $\rm (DSB–AM)$ with carrier is present.

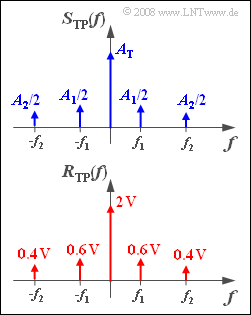
The upper graph shows the spectrum $S_{\rm TP}(f)$ of the equivalent low-pass signal in schematic form. This means, that the lengths of the Dirac lines drawn do not correspond to the actual values of $A_{\rm T}$, $A_1/2$ and $A_2/2$ .

The spectral function $R(f)$ of the received signal was measured. In the lower graph we can observe the equivalent low-pass spectrum $R_{\rm TP}(f)$ calculated from this.

The channel frequency response is characterised with sufficient accuracy with a few auxiliary values:

$$ H_{\rm K}(f = f_{\rm T}) = 0.5,$$

$$H_{\rm K}(f = f_{\rm T} \pm f_1) = 0.4,$$

$$ H_{\rm K}(f = f_{\rm T} \pm f_2) = 0.2 \hspace{0.05cm}.$$

Hints:

This exercise belongs to the chapternbsp; Envelope Demodulation.
Particular reference is made to the page Description using the equivalent low-pass signal.

Questions

$A_{\rm T} \ = \hspace{0.17cm} $

$\ \rm V$

$A_1 \ = \ $

$\ \rm V$

$A_2 \ = \ $

$\ \rm V$

	No distortion.
	Linear distortions.
	Nonlinear distortions.

	$r_{\rm TP}(t)$ is always real,
	$r_{\rm TP}(t)$ is always greater than or equal to zero,
	the phase function $ϕ(t)$ can take on the values $0^\circ$ and $180^\circ$ .

	No distortion.
	Linear distortions.
	Nonlinear distortions.

Solution

(1) Anhand der Grafiken auf der Angabenseite sind folgende Aussagen möglich:

$${A_{\rm T}} \cdot 0.5 = 2 \,{\rm V}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}A_{\rm T} \hspace{0.15cm}\underline {= 4 \,{\rm V}},$$

$${A_{\rm 1}}/{2} \cdot 0.4 = 0.6\,{\rm V}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}A_{\rm 1} \hspace{0.15cm}\underline {= 3 \,{\rm V}},$$

$${A_{\rm 2}}/{2} \cdot 0.2 = 0.4\,{\rm V}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}A_{\rm 2} \hspace{0.15cm}\underline {= 4 \,{\rm V}}\hspace{0.05cm}.$$

(2) Richtig ist der Lösungsvorschlag 3:

Der Modulationsgrad ergibt sich zu $m = (A_1 + A_2)/A_T = 1.75$.
Damit ergeben sich bei Verwendung eines Hüllkurvendemodulators starke nichtlineare Verzerrungen.
Ein Klirrfaktor kann aber nicht angegeben werden, da das Quellensignal zwei Frequenzanteile beinhaltet.

(3) Richtig sind die Aussagen 1 und 2:

Die Fourierrücktransformation von $R_{\rm TP}(f)$ führt zum Ergebnis:

$$ r_{\rm TP}(t) = 2 \,{\rm V} + 1.2 \,{\rm V} \cdot \cos(2 \pi f_1 t ) + 0.8 \,{\rm V} \cdot \cos(2 \pi f_2 t )\hspace{0.05cm}.$$

Diese Funktion ist stets reell und nicht–negativ.
Damit gilt gleichzeitig $ϕ(t) = 0$. Dagegen ist $ϕ(t) = 180^\circ$ nicht möglich.

(4) Ein Vergleich der beiden Signale

$$q(t) = 3 \,{\rm V} \cdot \cos(2 \pi f_1 t ) + 4 \,{\rm V} \cdot \cos(2 \pi f_2 t ),$$

$$ v(t) = 0.4 \cdot 3 \,{\rm V} \cdot \cos(2 \pi f_1 t ) + 0.2 \cdot 4 \,{\rm V} \cdot \cos(2 \pi f_2 t )$$

zeigt, dass nun lineare Verzerrungen – genauer gesagt Dämpfungsverzerrungen – auftreten ⇒ Lösungsvorschlag 2.

Der Kanal $H_{\rm K}(f)$ hat hier den positiven Effekt, dass anstelle von irreversiblen nichtlinearen Verzerrungen nun lineare Verzerrungen entstehen, die durch ein nachgeschaltetes Filter eliminiert werden können.
Dies ist darauf zurückzuführen, dass durch die stärkere Dämpfung des Quellensignals $q(t)$ im Vergleich zum Trägersignal $z(t)$ der Modulationsgrad von $m = 1.75$ auf $m = (0.4 · 3 \ \rm V + 0.2 · 4 \ \rm V)/(0.5 · 4 \ \rm V) = 1$ herabgesetzt wird.