Contents
Relationship between PDF and CDF
To describe random variables, in addition to the probability density function (PDF), we also use the cumulative distribution function (CDF) which is defined as follows:
$\text{Definition:}$ The cumulative distribution function $F_{x}(r)$ corresponds to the probability that the random variable $x$ is less than or equal to a real number value $r$ :
- $$F_{x}(r) = {\rm Pr}( x \le r).$$
For a continuous random variable, the following statements are possible regarding the CDF:
- The CDF is computable from the probability density function $f_{x}(x)$ by integration. It holds:
- $$F_{x}(r) = \int_{-\infty}^{r}f_x(x)\,{\rm d}x.$$
- Since the PDF is never negative, $F_{x}(r)$ increases at least weakly monotonically, and always lies between the following limits:
- $$F_{x}(r → \hspace{0.05cm} - \hspace{0.05cm} ∞) = 0, \hspace{0.5cm}F_{x}(r → +∞) = 1.$$
- Inversely, the probability density function can be determined from the CDF by differentiation:
- $$f_{x}(x)=\frac{{\rm d} F_{x}(r)}{{\rm d} r}\Bigg |_{\hspace{0.1cm}r=x}.$$
- The addition "$r = x$" makes it clear that in our nomenclature the argument of the probability density function is the random variable itself, while the CDF argument specifies any real variable $r$ .
$\text{Nomenclature Notes:}$
If in the definitions of $\rm PDF$ and $\rm CDF$ we had distinguished between the random variable $X$ and the realizations $x ∈ X$ ⇒ $f_{X}(x), F_{X}(x)$, we would have the following nomenclature:
- $$F_{X}(x) = {\rm Pr}(X \le x) = \int_{-\infty}^{x}f_{x}(\xi)\,{\rm d}\xi.$$
Unfortunately, at the beginning of our $\rm LNTwww$ project (2001) we decided to use our nomenclature for quite legitimate reasons, which now (2017) cannot be changed, also with regard to the realized learning videos.
So we stick with $f_{x}(x)$ instead of $f_{X}(x)$ as well as $F_{x}(r)$ instead of $F_{X}(x).$
CDF for continuous random variables
The equations given in the last section apply only to continuous-valued random variables and will be illustrated here by an example. In the next section it will be shown that for discrete random variables the equations must be modified somewhat.
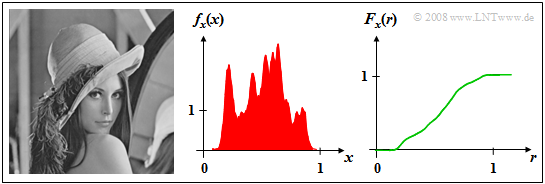
$\text{Example 1:}$ The left image shows the photo "Lena", which is often used as a test template for image coding procedures.
- If this image is divided into $256 × 256$ image pixels (pixels), and the brightness is determined for each pixel, a sequence $〈x_ν〉$ of gray values is obtained whose length $N = 256^2 = 65536$ .
- The gray value $x$ is a continuous value random variable, where the assignment to numerical values is arbitrary. For example, let "black" be characterized by the value $x = 0$ and "white" by $x = 1$ .
- The numerical value $x =0.5$ then characterizes a medium gray coloration.
The middle image shows the PDF $f_{x}(x)$ which is also often referred to in the literature as "gray value statistics" .
- It can be seen that in the original image some gray values are preferred and the two extreme values $x =0$ ("deep black") or $x =1$ ("pure white") occur very rarely.
- The distribution function $F_{x}(r)$ of this continuous random variable is continuous and increases monotonically from $0$ to $1$ as the right figure shows. For $r \approx 0$ and $r \approx 1$ the CDF is horizontal due to the lack of PDF components.
Note: Strictly speaking, for an image that can be displayed on a computer - in contrast to an "analog" photograph - the gray value is always a discrete value random variable. However, with large resolution of the color information ("color depth"), this random variablecan be approximated to be continuous in value.
The topic of this chapter is illustrated with examples in the (German language) learning video Zusammenhang zwischen WDF und VTF $\Rightarrow$ relationship between PDF and CDF.
Verteilungsfunktion bei diskreten Zufallsgrößen
Für die Berechnung der Verteilungsfunktion einer wertdiskreten Zufallsgröße $x$ aus deren WDF muss stets von einer allgemeineren Gleichung ausgegangen werden. Hier gilt mit mit der Hilfsvariablen $\varepsilon > 0$:
- $$F_{x}(r)=\lim_{\varepsilon\hspace{0.05cm}\to \hspace{0.05cm}0}\int_{-\infty}^{r+\varepsilon}f_x(x)\,{\rm d}x.$$
- Die Berechnung der Verteilungsfunktion durch Grenzwertbildung ist aufgrund des „≤”–Zeichens in der allgemeinen Definition erforderlich.
- Berücksichtigt man zudem, dass bei einer diskreten Zufallsgröße die WDF aus einer Summe gewichteter Diracfunktionen besteht, so erhält man:
- $$F_{x}(r)=\lim_{\varepsilon\hspace{0.05cm}\to \hspace{0.05cm} 0}\int_{-\infty}^{r+\varepsilon}\sum\limits_{\mu= 1}^{ M}p_\mu\cdot \delta(x-x_\mu)\,{\rm d}x.$$
- Vertauscht man in dieser Gleichung Integration und Summation, und berücksichtigt, dass die Integration über die Diracfunktion die Sprungfunktion ergibt, so erhält man:
- $$F_{x}(r)=\sum\limits_{\mu= \rm 1}^{\it M}p_\mu\cdot \gamma_0 (r-x_\mu),\hspace{0.4cm}{\rm mit} \hspace{0.4cm}\gamma_0(x)=\lim_{\epsilon\hspace{0.05cm}\to \hspace{0.05cm} 0}\int_{-\infty}^{x+\varepsilon}\delta (u)\,{\rm d} u = \left\{ \begin{array}{*{2}{c}} 0 \hspace{0.4cm} {\rm falls}\hspace{0.1cm} x< 0,\\ 1 \hspace{0.4cm} {\rm falls}\hspace{0.1cm}x\ge 0. \\ \end{array} \right.$$
Hierzu ist anzumerken:
- $γ_0(x)$ unterscheidet sich von der in der Systemtheorie üblichen Sprungfunktion $γ(x)$ dadurch, dass an der Sprungstelle $x = 0$ der rechtsseitige Grenzwert "Eins" gültig ist (anstelle des Mittelwertes "$1/2$" zwischen links- und rechtsseitigem Grenzwert).
- Mit obiger VTF-Definition gilt dann für die Wahrscheinlichkeit von kontinuierlichen und diskreten Zufallsgrößen gleichermaßen, und natürlich auch für gemischte Zufallsgrößen mit diskreten und kontinuierlichen Anteilen:
- $${\rm Pr}(x_{\rm u}<x \le x_{\rm o})=F_x(x_{\rm o})-F_x(x_{\rm u}).$$
- Bei rein kontinuierlichen Zufallsgrößen könnten hier das „Kleiner”–Zeichen und das „Kleiner/Gleich”–Zeichen gegenseitig ersetzt werden.
- $${\rm Pr}(x_{\rm u}<x \le x_{\rm o}) ={\rm Pr}(x_{\rm u}\le x \le x_{\rm o}) ={\rm Pr}(x_{\rm u}\le x < x_{\rm o}) ={\rm Pr}(x_{\rm u}<x < x_{\rm o}).$$
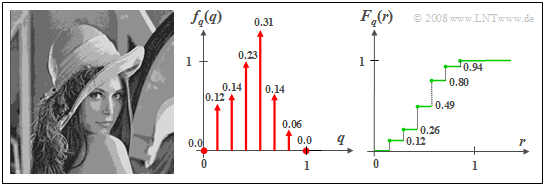
$\text{Beispiel 2:}$ Wird der Grauwert des ursprünglichen Lena–Fotos mit acht Stufen quantisiert, so dass jedes einzelne Pixel durch drei Bit dargestellt und digital übertragen werden kann, so ergibt sich die diskrete Zufallsgröße $q$. Durch die Quantisierung geht allerdings ein Teil der Bildinformation verloren, was sich im quantisierten Bild durch deutlich erkennbare „Konturen” auswirkt.
- Die dazugehörige Wahrscheinlichkeitsdichtefunktion $f_{q}(q)$ setzt sich aus $M = 8$ Diracfunktionen zusammen, wobei bei der hier gewählten Quantisierung den möglichen Graustufen die Werte $q_\mu = (\mu – 1)/7$ mit $\mu = 1, 2,$ ... , $8$ zugeordnet sind.
- Die Gewichte der Diracfunktionen kann man aus der WDF $f_{x}(x)$ des Originalbildes berechnen. Man erhält
- $$p_\mu={\rm Pr}(q = q_\mu ) = {\rm Pr}(\frac{2\mu-\rm 3}{14}< {x} \le\frac{2\it \mu- \rm 1}{14}) \rm = \int_{(2\it \mu- \rm 3)/14}^{(2\mu-1)/14}\it f_{x}{\rm (}x{\rm )}\,{\rm d}x.$$
- Für die undefinierten Randbereiche $(x<0$ bzw. $x>1)$ ist hier jeweils $f_{x}(x) = 0$ zu setzen.
- Da im Originalbild die Graustufen $x ≈0$ („sehr tiefes Schwarz”) bzw. $x ≈1$ („nahezu reines Weiß”) weitgehend fehlen, ergeben sich die Wahrscheinlichkeiten $p_1 ≈ p_8 ≈ 0$, und in der WDF sind tatsächlich nur sechs Diracfunktionen sichtbar. Diese beiden fehlenden Diracfunktionen bei $q = 0$ und $q =1$ sind in der mittleren Grafik nur durch Punkte angedeutet.
- Die rechts skizzierte Verteilungsfunktion $F_{q}(r)$ weist somit sechs Unstetigkeitsstellen auf, bei denen jeweils der rechtsseitige Grenzwert gültig ist.
Die in diesem Abschnitt behandelte Thematik ist im Lernvideo Zusammenhang zwischen WDF und VTF zusammengefasst.
Aufgaben zum Kapitel
Aufgabe 3.2: $\cos^2$– und Dirac–VTF
Aufgabe 3.2Z: Zusammenhang zwischen WDF und VTF