Cumulative Distribution Function

Relationship between PDF and CDF

To describe random variables, in addition to the probability density function $\rm (PDF)$, we also use the cumulative distribution function $\rm (CDF)$ which is defined as follows:

$\text{Definition:}$ The cumulative distribution function $F_{x}(r)$ corresponds to the probability that the random variable $x$ is less than or equal to a real number $r$:

$$F_{x}(r) = {\rm Pr}( x \le r).$$

For a continuous random variable, the following statements are possible regarding the CDF:

The CDF is computable from the probability density function $f_{x}(x)$ by integration. It holds:

$$F_{x}(r) = \int_{-\infty}^{r}f_x(x)\,{\rm d}x.$$

Since the PDF is never negative, $F_{x}(r)$ increases at least weakly monotonically, and always lies between the following limits:

$$F_{x}(r → \hspace{0.05cm} - \hspace{0.05cm} ∞) = 0, \hspace{0.5cm}F_{x}(r → +∞) = 1.$$

Inversely, the probability density function can be determined from the CDF by differentiation:

$$f_{x}(x)=\frac{{\rm d} F_{x}(r)}{{\rm d} r}\Bigg |_{\hspace{0.1cm}r=x}.$$

The addition "$r = x$" makes it clear that in our nomenclature the PDF argument is the random variable itself, while the CDF argument specifies any real variable $r$ .

$\text{Nomenclature Notes:}$

If in the definitions of $\rm PDF$ and $\rm CDF$ we had distinguished

between the random variable $X$
and the realizations $x ∈ X$ ⇒ $f_{X}(x), F_{X}(x)$,

we would have the following nomenclature:

$$F_{X}(x) = {\rm Pr}(X \le x) = \int_{-\infty}^{x}f_{x}(\xi)\,{\rm d}\xi.$$

Unfortunately, at the beginning of our $\rm LNTwww$ project (2001) we decided to use our nomenclature for quite legitimate reasons,&nbsp which now (2017) cannot be changed, also with regard to the realized learning videos.

So we stick with $f_{x}(x)$ instead of $f_{X}(x)$ as well as $F_{x}(r)$ instead of $F_{X}(x).$

CDF for continuous-valued random variables

The equations given in the last section apply only to continuous-valued random variables and will be illustrated here by an example. In the next section it will be shown that for discrete-valued random variables the equations must be modified somewhat.

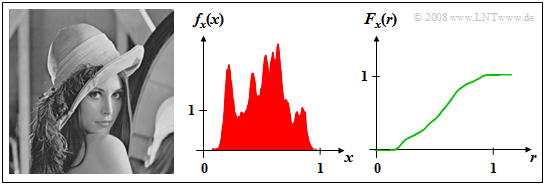
$\text{Example 1:}$ The left image shows the photo "Lena", which is often used as a test template for image coding procedures.

PDF and CDF of a continuous-valued image

If this image is divided into $256 × 256$ (image) pixels, and the brightness is determined for each pixel, a sequence $〈x_ν〉$ of gray values is obtained whose length $N = 256^2 = 65536$.
The gray value $x$ is a continuous-valued random variable, where the assignment to numerical values is arbitrary. For example, let "black" be characterized by the value $x = 0$ and "white" by $x = 1$.
The numerical value $x =0.5$ then characterizes a medium gray coloration.

The middle image shows the PDF $f_{x}(x)$ which is also often referred to in the literature as "gray value statistics" .

It can be seen that in the original image some gray values are preferred and the two extreme values $x =0$ ("deep black") or $x =1$ ("pure white") occur very rarely.
The distribution function $F_{x}(r)$ of this continuous random variable is continuous and increases monotonically from $0$ to $1$ as the right figure shows. For $r \approx 0$ and $r \approx 1$ the CDF is horizontal due to the lack of PDF components.

Note: Strictly speaking, for an image that can be displayed on a computer - in contrast to an "analog" photograph - the gray value is always a discrete value random variable. However, with large resolution of the color information ("color depth"), this random variablecan be approximated to be continuous in value.

The topic of this chapter is illustrated with examples in the (German language) learning video Zusammenhang zwischen WDF und VTF $\Rightarrow$ relationship between PDF and CDF.

CDF for discrete-valued random variables

For the calculation of the distribution function of a discrete value random variable $x$ from its PDF, a more general equation must always be assumed Here, with the auxiliary variable $\varepsilon > 0$:

$$F_{x}(r)=\lim_{\varepsilon\hspace{0.05cm}\to \hspace{0.05cm}0}\int_{-\infty}^{r+\varepsilon}f_x(x)\,{\rm d}x.$$

Calculation of the distribution function by boundary value formation is required due to the "≤"–sign in the general definition .
If we also take into account that, for a discrete random variable, the PDF consists of a sum of weighted Dirac functions , we obtain:

$$F_{x}(r)=\lim_{\varepsilon\hspace{0.05cm}\to \hspace{0.05cm} 0}\int_{-\infty}^{r+\varepsilon}\sum\limits_{\mu= 1}^{ M}p_\mu\cdot \delta(x-x_\mu)\,{\rm d}x.$$

If we interchange integration and summation in this equation, and consider that integration over the Dirac function yields the step function, we obtain:

$$F_{x}(r)=\sum\limits_{\mu= \rm 1}^{\it M}p_\mu\cdot \gamma_0 (r-x_\mu),\hspace{0.4cm}{\rm with} \hspace{0.4cm}\gamma_0(x)=\lim_{\epsilon\hspace{0.05cm}\to \hspace{0.05cm} 0}\int_{-\infty}^{x+\varepsilon}\delta (u)\,{\rm d} u = \left\{ \begin{array}{*{2}{c}} 0 \hspace{0.4cm} {\rm if}\hspace{0.1cm} x< 0,\\ 1 \hspace{0.4cm} {\rm if}\hspace{0.1cm}x\ge 0. \\ \end{array} \right.$$

It should be noted that:

$γ_0(x)$ differs from the usual in systems theory unit step function $γ(x)$ in that at the jump point $x = 0$ the right-hand side limit "one" is valid (instead of the mean value "$1/2$" between left- and right-hand side limits).
With the above CDF definition, then, for the probability of continuous and discrete random variables equally, and of course also for mixed random variables with discrete and continuous parts:

$${\rm Pr}(x_{\rm u}<x \le x_{\rm o})=F_x(x_{\rm o})-F_x(x_{\rm u}).$$

For purely continuous random variables, the "less than" sign and the "less than/equal to" sign could be substituted for each other here.

$${\rm Pr}(x_{\rm u}<x \le x_{\rm o}) ={\rm Pr}(x_{\rm u}\le x \le x_{\rm o}) ={\rm Pr}(x_{\rm u}\le x < x_{\rm o}) ={\rm Pr}(x_{\rm u}<x < x_{\rm o}).$$

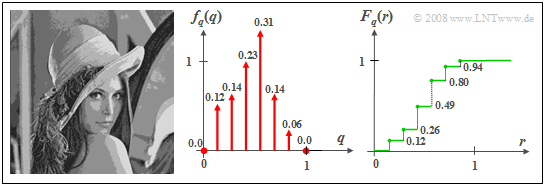
$\text{Example 2:}$ If the gray value of the original Lena photo is quantized by eight levels, so that each pixel can be represented by three bits and transmitted digitally, the discrete random variable $q$ is obtained. However, due to the quantization, a part of the image information is lost, which is reflected in the quantized image by clearly recognizable "contours".

PDF and CDF of a discrete value image

The associated probability density function $f_{q}(q)$ is composed of $M = 8$ Dirac functions, where, in the quantization chosen here, the possible gray levels are assigned the values $q_\mu = (\mu - 1)/7$ with $\mu = 1, 2,$ ... , $8$ are assigned.
The weights of the Dirac functions can be calculated from the PDF $f_{x}(x)$ of the original image. One obtains

$$p_\mu={\rm Pr}(q = q_\mu ) = {\rm Pr}(\frac{2\mu-\rm 3}{14}< {x} \le\frac{2\it \mu- \rm 1}{14}) \rm = \int_{(2\it \mu- \rm 3)/14}^{(2\mu-1)/14}\it f_{x}{\rm (}x{\rm )}\,{\rm d}x.$$

For the undefined border areas $(x<0$ resp. $x>1)$ is to be set here respectively $f_{x}(x) = 0$ .
Since in the original image the gray levels $x ≈0$ ("very deep black") or $x ≈1$ ("almost pure white") are largely missing, the probabilities $p_1 ≈ p_8 ≈ 0$ result, and in fact only six Dirac functions are visible in the PDF. These two missing Dirac functions at $q = 0$ and $q =1$ are only indicated by dots in the middle graph.

The distribution function sketched on the right $F_{q}(r)$ thus has six points of discontinuity, where the right-hand side limit is valid in each case

.

The topic of this chapter is illustrated with examples in the (German language) learning video Zusammenhang zwischen WDF und VTF $\Rightarrow$ relationship between PDF and CDF.

Exercises for the chapter

Exercise 3.2: cos²-CDF and CDF with Step Functions

Exercise 3.2Z: Relationship between PDF and CDF

Cumulative Distribution Function

Contents

Relationship between PDF and CDF

CDF for continuous-valued random variables

CDF for discrete-valued random variables

Exercises for the chapter