Exercise 3.2Z: Relationship between PDF and CDF

• Return to book

Given CDF  $ F_x(r)$

Given is the random variable  $x$  with the cumulative distribution function  $\rm (CDF)$.

$$ F_x(r)=\left\{\begin{array}{*{4}{c}} 0.25\cdot {\rm e}^{2\it r} &\rm for\hspace{0.1cm}\it r<\rm 0, \\ 1-0.25\cdot {\rm e}^{-2\it r} & \rm for\hspace{0.1cm}\it r\ge\rm 0. \\\end{array}\right.$$

• This function is shown on the right.
• It can be seen that at the unit step point  $r = 0$  the right-hand side limit is valid.

Hints:

• The exercise belongs to the chapter  Cumulative Distribution Function.
• Reference is made to the chapter  Probability Density Function.
• The topic of this chapter is illustrated with examples in the  (German language)  learning video
      "Zusammenhang zwischen WDF und VTF"   $\Rightarrow$   "Relationship between PDF and CDF".

Questions

1

What properties of the CDF hold when the random variable has no limits?

	The CDF increases from  $0$  to  $1$  at least weakly monotonically.
	The  $F_x(r)$ values  $0$  and  $1$  are possible for finite  $r$values.
	A horizontal section indicates that in this range the random size has no proportions.
	Vertical sections are possible.

2

What is the probability that  $x$  is positive?

${\rm Pr}(x > 0) \ = \ $

3

What is the probability that  $|\hspace{0.05cm}x\hspace{0.05cm}|$  is larger than  $0.5$?

${\rm Pr}(|\hspace{0.05cm}x\hspace{0.05cm}| > 0.5) \ = \ $

4

Specify the associated PDF  $f_x(x)$  in general and the value for  $x = 1$.

$f_x(x =1)\ = \ $

5

What is the probability that  $x$  is exactly equal to  $1$ ?

${\rm Pr}(x = 1)\ = \ $

6

What is the probability that  $x$  is exactly equal to  $0$ ?

${\rm Pr}(x = 0)\ = \ $

Solution

Solution

(1)  The statements 1, 3 and 4 are always correct:

• A horizontal intercept in the VTF indicates that the random size has no values in that region.
• In contrast, a vertical intercept in the VTF indicates a Dirac function in the WDF  $($at the same location  $x_0)$ .
• This means that the random size takes the value  $x_0$  very frequently, namely with finite probability.
• All other values occur exactly with probability  $0$ .
• If, however  $x$  is limited to the range from  $x_{\rm min}$  to  $x_{\rm max}$  then  $F_x(r) = 0$  für  $r < x_{\rm min}$  and  $F_x(r) = 1$  für  $r > x_{\rm max}$.
• In this special case, the second statement would also be true.

(2)  The sought probability can be calculated from the difference of the VTF–values at the boundaries:

$${\rm Pr}( x> 0)= F_x(\infty)- F_x(\rm 0) \hspace{0.15cm}\underline{=\rm 0.25}.$$

(3)  For the probability that  $x$  is greater than  $0.5$  holds:

$${\rm Pr}(x> 0.5)=1- F_x(0.5)=\rm 0.25\cdot e^{-1} \hspace{0.15cm}{\approx0.092}. $$

• For reasons of symmetry ${\rm Pr}(x<- 0.5)$  is just as large. From this follows:

$${\rm Pr}( |\hspace{0.05cm} x\hspace{0.05cm}| >\rm 0.5) \hspace{0.15cm}\underline{= \rm 0.184}.$$

PDF of Laplace distribution

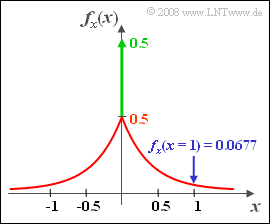
(4)  The PDF is obtained from the corresponding CDF by differentiating the two areas.

• The result is a two-sided exponential function as well as a Dirac function at  $x = 0$ :

$$f_x(x)=\rm 0.5\cdot \rm e^{-2\cdot |\hspace{0.05cm}\it x\hspace{0.05cm}|} + \rm 0.5\cdot\delta(\it x).$$

• The numerical value we are looking for is  $f_x(x = 1)\hspace{0.15cm}\underline{= \rm 0.0677}$.

Note:   The two-sided exponential distribution is also called "Laplace distribution".

(5)  In the range around  $1$  describes  $x$  a continuous random size.

• The probability that  $x$  has exactly the value  $1$  is therefore  ${\rm Pr}(x = 1)\hspace{0.15cm}\underline{= \rm 0}.$

(6)  In  $50\%$  of time will  $x = 0$  hold:   ${\rm Pr}(x = 0)\hspace{0.15cm}\underline{= \rm 0.5}.$

Notes:

• The PDF of a speech signal is often described by a two-sided exponential function.
• The Dirac function at  $x = 0$  mainly takes into account speech pauses – here in  $50\%$  all times.