Exercise 3.1Z: Influence of the Message Phase in Phase Modulation
We will now consider the phase modulation of diverse oscillations
- $$ q(t) = \cos(\omega_{\rm N} \cdot t + \phi_{\rm N})\hspace{0.05cm}.$$
The source signal is represented here in normalized form with $($amplitude $1)$ , so that the phase-modulated signal can be characterised by the modulation index (or phase deviation) $η$ as follows:
- $$s(t) = A_{\rm T} \cdot \cos \hspace{-0.1cm}\big[\omega_{\rm T} \cdot t + \eta \cdot q(t) \big]\hspace{0.05cm}.$$
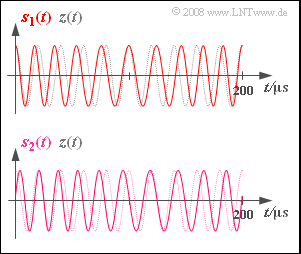
- The signal $s_1(t)$ shown in the upper graph is characterized by the paramet values $ϕ_{\rm N} = -90^\circ$ und $η_1 = 2$ .
- The frequency $f_{\rm N}$ of this sinusoidal source signal as well as the carrier frequency $f_{\rm T}$ can be determined from the signal section of duration $200 \ \rm µ s$ represented here.
- The signal $s_2(t)$ possibly differs from $s_1(t)$ due to a different message phase $ϕ_{\rm N}$ and modulation index $η$. All other system parameters are unchanged from $s_1(t)$ .
Hints:
- This exercise belongs to the chapter Phase Modulation.
- Particular reference is made to the page Signal characteristics of phase modulation.
Questions
Musterlösung
- Zu den Zeitpunkten $t = 0$, $t = 100 \ \rm µ s$ und $t = 200 \ \rm µ s$ sind die Signale $z(t)$ und $s(t)$ phasensynchron.
- In der ersten Halbwelle von $q(t)$ kommen die Nulldurchgänge von $s(t)$ etwas früher als die des Trägersignals $z(t)$ ⇒ positive Phase.
- Dagegen ist im Bereich von $t = 100 \ \rm µ s$ bis $t = 200 \ \rm µ s$ die Phase $ϕ(t) < 0$.
(2) Es gilt $f_{\rm T}\hspace{0.15cm}\underline{ = 50 \ \rm kHz}$,
- da im dargestellten $z(t)$–Signalausschnitt der Dauer $200 \ \rm µ s$ genau $10$ Perioden abgezählt werden können.
(3) Die maximale relative Phasenabweichung beträgt $ϕ_{\rm max} = η_1/(2π)\hspace{0.15cm}\underline{ ≈ 0.318}$.
(4) Da die Periodendauer des Trägers $T_0 = 20 \ \rm µ s$ ist, erhält man $Δt_{\rm max} = ϕ_{\rm max} ·T_0\hspace{0.15cm}\underline{ ≈ 6.37 \ \rm µ s}$.
(5) Die maximale Phasenabweichung (Verschiebung der Nulldurchgänge) ist bei $s_2(t)$ genau so groß wie bei $s_1(t)$.
- Daraus kann auf $η_2 = η_1\hspace{0.15cm}\underline{ = 2}$ geschlossen werden.
(6) Das Signal $s_2(t)$ ist gegenüber $s_1(t)$ um $25 \ \rm µ s$ nach rechts verschoben. Deshalb muss auch für die Quellensignale gelten:
- $$ q_2(t) = q_1(t - 25\,{\rm \mu s}) = \cos \hspace{-0.1cm} \big[2 \pi f_{\rm N} (t - 25\,{\rm \mu s}) \big ] = \cos (\omega_{\rm N} \cdot t - 0.75 \cdot \pi)\hspace{0.05cm}.$$
- Dies entspricht der Phasenlage $ϕ_{\rm N2}\hspace{0.15cm}\underline{ = -135^\circ}$.