Contents
Signal-to-noise power ratio in PM
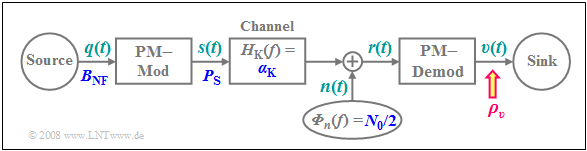
To investigate noise behavior, we will take the AWGN channel as our starting point and calculate the sink SNR $ρ_v$ as a function of
- the frequency (bandwidth) $B_{\rm NF}$ of the cosine source signal,
- the transmit power $P_{\rm S}$,
- the channel transmission factor $α_{\rm K}$, and
- the (one-sided) noise power density $N_0$.
The principle procedure is described in detail in the section Investigations at the AWGN channel :
If the performance parameter
- $$\xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}$$
is sufficiently large, the follwoing approximatino is obtained for phase modulation with modulation index $η$ :
- $$\rho_{v } \approx {\eta^2}/{2} \cdot\xi \hspace{0.05cm}.$$
This means that for phase modulation, the sink SNR increases quadratically with increasing $η$ .
The exact calculation of $ρ_v$ is not very simple, and is also laborious. Here, we will only briefly describe the calculation steps:
- One approximates the white noise $n(t)$ for the bandwidth $B_{\rm HF}$ by a sum of sinusoidal interferences spaced by $f_{\rm St}$ (see second sketch in the following section).
- One calculates the S/N ratio after demodulation for each sinusoidal interference and sums the individual contributions,which are now all in the low-pass region $|f| < B_{\rm NF}$ .
- The above simple result is obtained after the boundary transition $f_{\rm St} → 0$. The sum then turns into an integral and this can be solved approximately.
Signal-to-noise power ratio in FM
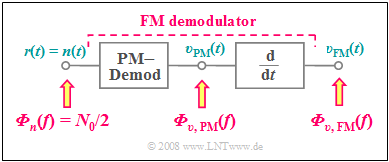
For calculation one uses the fact that the FM demodulator can be realized with a PM demodulator and a differentiator.
- The block diagram on the right refers only to the noise signals ⇒ $s(t) = 0$.
- Thus the received signal $r(t) = n(t)$, where we assume additive Gaussian white noise with center frequency $f_{\rm T}$ and bandwidth $B_{\rm HF}$ for $n(t)$ .
When calculating the noise power density after the FM demodulator, consider:
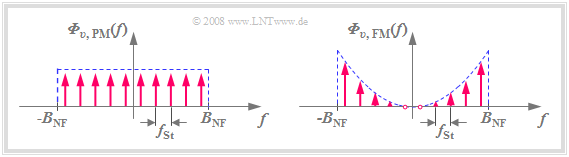
- The noise power density ${\it Φ}_{v,\hspace{0.05cm}{\rm PM}}(f)$ after the PM demodulator is in the low-pass range, has the (one-sided) bandwidth $B_{\rm NF}$ and is also "white"
(see left plot in the graph below). - The power density at the output of a linear system with frequency response $H(f)$ when the noise power density ${\it Φ}_{v,\hspace{0.05cm}{\rm PM}}(f)$ is applied to the input is generally:
- $${ \it \Phi}_{v {\rm , \hspace{0.05cm}FM} } (f) = { \it \Phi}_{v {\rm , \hspace{0.05cm}PM} } (f) \cdot |H(f)|^2 \hspace{0.05cm}.$$
- The differentiator is just such a linear system. Its frequency response $H(f)$ increases linearly with $f$ , and it is applied to the noise power density at the output of the FM demodulator (see the right plot in the lower graph):
- $${ \it \Phi}_{v {\rm , \hspace{0.05cm}FM} } (f) = {\rm const. } \cdot f^2 \cdot { \it \Phi}_{v {\rm , \hspace{0.05cm}PM} }(f) \hspace{0.05cm}.$$
$\rm Conclusion\text{:}$ Taking this result into account, one arrives at the following sink SNR (if the performance parameter $ξ$ is sufficiently large) after a longer calculation:
- $$\rho_{v } \approx \frac{3\cdot \eta^2}{2} \cdot \frac{\alpha_{\rm K}^2 \cdot P_{\rm S} }{N_0 \cdot B_{\rm NF} } = 3/2 \cdot{\eta^2} \cdot\xi \hspace{0.05cm}.$$
The graph illustrates:
- The noise power density ${\it Φ}_{v,\hspace{0.05cm}{\rm FM} }(f)$ is not white, unlike Gegensatz zu ${\it Φ}_{v,\hspace{0.05cm}{\rm PM} }(f)$ .
- Rather, ${\it Φ}_{v,\hspace{0.05cm}{\rm FM} }(f)$ increases quadratically towards the limits $(\pm B_{\rm NF} )$ .
- When $f = 0$ , ${\it Φ}_{v,\hspace{0.05cm}{\rm FM} }(f)$ has no noise components.
Systemvergleich von AM, PM und FM hinsichtlich Rauschen
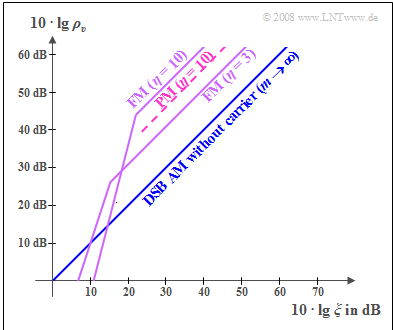
Wie schon im Abschnitt Untersuchungen beim AWGN-Kanal ausführlich erläutert und im Abschnitt Sinken-SNR und Leistungskenngröße auf die Amplitudenmodulation angewendet, betrachten wir wieder die doppelt-logarithmische Darstellung des Sinken–SNR $ρ_v$ über der Kenngröße
- $$\xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}.$$
Diese qualitativ zu verstehenden Kurven sind wie folgt zu interpretieren:
- Die Vergleichskurve liefert die ZSB–AM ohne Träger ⇒ Modulationsgrad $m → ∞$. Hier gilt $ρ_v = ξ$ und auch bei doppelt–logarithmischer Darstellung ergibt sich eine $45^\circ$–Gerade durch den Ursprung.
- Die FM–Kurve mit $η = 3$ liegt um $10 · \lg \ 13.5 ≈ 11.3 \ \rm dB$ über der AM–Kurve. Anschaulich kann man das bessere Rauschverhalten der Frequenzmodulation dadurch erklären, dass ein additiver Rauschanteil die Lage der Nulldurchgänge weniger beeinflusst als er die Amplitudenwerte verändert.
- Ist das wirksame Rauschen sehr groß und damit die Leistungskenngröße klein $(10 · \lg \ ξ ≤ 15 \ \rm dB)$, so ist Winkelmodulation nicht zu empfehlen. Aufgrund des Rauschens können dann Nulldurchgänge völlig verschwinden und so deren Detektion unmöglich machen. Man spricht vom "FM–Knick".
- Hinsichtlich Rauschen ist bei jeder Art von Winkelmodulation ein möglichst großer Modulationsindex anzustreben. So liegt die Kurve für $η = 10$ um etwa $10.4 \ \rm dB$ über der Kurve für $η = 3$. Zu berücksichtigen ist allerdings, dass ein größeres $η$ auch eine größere Bandbreite erfordert oder – bei gegebener Kanalbandbreite – stärkere nichtlineare Verzerrungen hervorruft.
- Bei gleichem Modulationsindex ist die Phasenmodulation (PM) stets um $10 \cdot \lg \ 3 ≈ 4.8 \ \rm dB$ schlechter als die Frequenzmodulation (FM). Dies ist einer der Gründe, warum die analoge Phasenmodulation in der Praxis nur wenig Bedeutung hat. Dagegen wird bei digitaler Modulation die Variante Phase Shift Keying (PSK) aufgrund anderer Vorteile häufiger eingesetzt als Frequency Shift Keying (FSK).
- Alle angegebenen Kurven gelten quantitativ nur für eine harmonische Schwingung (also für nur eine einzige Frequenz). Bei einem Frequenzgemisch – das in der Praxis stets vorliegt – gelten die Kurven aber zumindest qualitativ.
Preemphase und Deemphase
Ein wichtiges Ergebnis der letzten Abschnitte war, dass das Sinken–SNR bei FM entsprechend $\rho_{v } \approx 1.5 \cdot{\eta^2} \cdot\xi \hspace{0.05cm}$ in guter Näherung quadratisch vom Modulationsindex abhängt. Da aber bei Frequenzmodulation der Modulationsindex $η$ umgekehrt proportional zur Nachrichtenfrequenz $f_{\rm N}$ ist, hängt auch das Sinken–SNR von $f_{\rm N}$ ab.
Daraus ergeben sich folgende Konsequenzen:
- Besteht das Nachrichtensignal aus mehreren Frequenzen, so weisen die höheren Frequenzen nach einer FM–Modulation einen kleineren Modulationsindex $η$ auf als die niedrigeren Frequenzen.
- Das bedeutet auch: Die höheren Frequenzanteile $($mit kleinerem $η)$ sind dementsprechend stärker verrauscht als niedrigere Frequenzen, wenn nicht besondere Maßnahmen getroffen werden.
Eine solche Maßnahme ist beispielsweise eine Preemphase. Dabei werden höhere Frequenzen durch ein Hochpass–Filternetzwerk $H_{\rm PE}(f)$ angehoben und für diese der Modulationsindex $η$ erhöht.
Die sendeseitige Preemphase muss beim Empfänger durch ein Netzwerk $H_{\rm DE}(f) = 1/H_{\rm PE}(f)$ rückgängig gemacht werden. Dieses Absenken der höheren Frequenzen nennt man Deemphase.
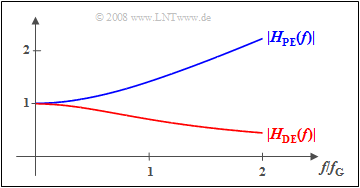
Die Grafik zeigt ein mögliches Beispiel für die Filterfunktionen von
- Preemphase (blau) ⇒ $|H_{{\rm PE} } (f)| = \sqrt{1 + \left({f}/{f_{\rm G}}\right)^2}\hspace{0.05cm},$
- Deemphase (rot) ⇒ $|H_{{\rm DE} } (f)| = |H_{{\rm PE} } (f)|^{-1} \hspace{0.05cm}.$
Aufgaben zum Kapitel
Aufgabe 3.10: Berechnung der Rauschleistungen
Aufgabe 3.10Z: Amplituden- und Winkelmodulation im Vergleich
Aufgabe 3.11: Preemphase und Deemphase